Introducción
Los profesionales que emiten pronósticos del tiempo para el público comprenden muy bien la importancia de examinar los pronósticos de varios modelos de PNT para producir pronósticos más confiables. Una de las formas de hacerlo consiste en comparar distintas predicciones numéricas. Esto se puede hacer, por ejemplo, comparando los pronósticos de los modelos globales con los regionales o comparando los pronósticos de los modelos usados en diferentes centros de PNT (por ejemplo, GFS, NOGAPS, GEM y ECMWF). También se pueden comparar los resultados de distintos ciclos de ejecución del mismo modelo para ver cómo los resultados cambian con el tiempo a medida que se introducen observaciones nuevas. El uso de conjuntos de pronósticos para hacer predicciones es una técnica relativamente nueva en el ámbito de pronóstico operativo que permite comparar múltiples pronósticos de un modelo rápidamente y sobre una base científica.
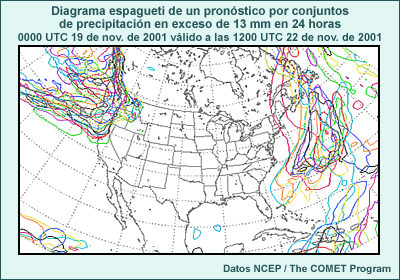
Los productos de un conjunto, como el diagrama espagueti de la figura anterior, se obtienen usando métodos gráficos y estadísticos para combinar múltiples ciclos de ejecución del modelo, cada uno basado en condiciones iniciales levemente distintas o en configuraciones y/o parametrizaciones ligeramente diferentes. Esto permite incluir información acerca del nivel de incertidumbre, los resultados de pronóstico más probables y las probabilidades de dichos resultados. Los productos de un conjunto representan una herramienta de PNT adicional que agrega un nivel de información para hacer un uso más informado de la orientación de PNT en el proceso de pronóstico.
Objetivos de la lección
Nuestro objetivo es que después de estudiar esta lección usted sepa:
- explicar las bases del pronóstico numérico por conjuntos y lo que significa decir que la atmósfera es caótica (es decir, sensible a las condiciones iniciales);
- describir la variedad de métodos empleados para generar los miembros del sistema de predicción por conjuntos, incluyendo los aspectos de perturbación de las condiciones iniciales, condiciones de frontera y configuraciones del modelo;
- entender los conceptos estadísticos básicos y los métodos usados en el desarrollo de los productos del conjunto, incluyendo las distribuciones de probabilidad, la centralidad, la variabilidad y las características de la forma de la distribución;
- reconocer e interpretar los distintos productos de predicción por conjuntos, incluyendo los gráficos de predicción puntuales y espaciales, y aquellos que muestran los regímenes de flujo, como los de medida relativa de predictibilidad (Relative Measure of Predictability, o RMOP), que revelan los sesgos y los errores de los modelos de PNT;
- interpretar los productos de verificación del conjunto y aplicarlos al uso de pronósticos por conjuntos.
Prerrequisitos
Para que pueda aprovechar mejor esta lección, usted debe estar familiarizado con los conceptos y procesos descritos en la serie de lecciones que componen el Curso de educación a distancia sobre PNT (NWP Distance Learning Course). En particular, esta lección supone un conocimiento general de los procesos de asimilación de datos (vea Comprensión de los sistemas de asimilación: cómo los modelos crean sus propias condiciones iniciales, versión 2, una lección sobre la asimilación de datos y la generación de las condiciones iniciales en los modelos) y comprende los conceptos de parametrización del modelo, condiciones de frontera y dinámica y estructura de los modelos.
Estructura de la lección
Aunque hemos hecho todo lo posible por resumir el contenido a fin de concentrarnos en los conocimientos esenciales que usted necesitará para fines de pronóstico, esta lección presenta un tema nuevo con aspectos muy complejos, de modo que es posible que tarde tres o más horas en completarla. Por esta razón le recomendamos que divida su tiempo de estudio en una serie de sesiones, y que trate cada una por separado.
- Esta sección introductoria continúa con la descripción de las ventajas de la predicción por conjuntos sobre los pronósticos individuales y muestra cómo se generan pronósticos por conjuntos aplicando la teoría del caos a la predicción numérica del tiempo.
- En la sección «Generación del conjunto» se analizan los métodos para crear el conjunto de ciclos de ejecución del modelo -los miembros del conjunto- que contribuirán a la predicción por conjuntos.
- Para sentar las bases para aprender a interpretar los resultados del conjunto, la sección «Conceptos estadísticos» describe conceptos clave de probabilidad y estadística y cómo se aplican para producir los datos del conjunto después de su procesamiento.
- La sección más larga de la lección, «Resumen de los datos», presenta varios productos comunes generados a base de los conjuntos y analiza su interpretación.
- La sección «Verificación» cubre las técnicas que le ayudarán a interpretar el rendimiento de la predicción por conjuntos y a entender posibles maneras de mejorar dichos pronósticos.
- Para profundizar sus estudios más allá de la lección, proporcionamos enlaces a ejemplos de aplicaciones específicas de los conjuntos en la Biblioteca de casos de estudio de PNT (en inglés).
En varias partes de la lección encontrará secciones «A fondo» que proporcionan información más detallada sobre los conceptos y procesos de la predicción por conjuntos. Lea estas secciones según sus necesidades, tiempo disponible e interés.
¿Por qué usar conjuntos?
De acuerdo con el plan quinquenal VISION 2005 del Servicio Nacional de Meteorología (National Weather Service, o NWS) de los Estados Unidos, para el año 2005 el NWS debe proporcionar pronósticos meteorológicos en términos probabilísticos. La predicción probabilística reflejará, aun en el corto plazo, lo que sabemos y lo que no sabemos acerca del comportamiento de la atmósfera y nuestra capacidad de modelarla con exactitud para fines de pronóstico del tiempo. Los pronósticos por conjuntos están diseñados para capturar las probabilidades de que se produzcan los eventos meteorológicos y el rango de incertidumbre inherente a cada situación de pronóstico, de modo que al generar un pronóstico sepamos lo que necesitamos comunicar al público.
Nota: aunque cómo transmitir la información de los pronósticos probabilísticos excede el ámbito de esta lección, esta consideración será de suma importancia a medida que pasemos a expresar los pronósticos en términos probabilísticos.
Ventajas del sistema de predicción por conjuntos sobre la PNT de un modelo individual
La siguiente tabla resume las ventajas de un sistema conjunto de pronósticos deterministas frente a un pronóstico determinista individual. Esta lista no es exhaustiva.
| Característica | Pronóstico individual | Sistema de pronóstico por conjuntos |
|
Incertidumbre en las condiciones iniciales |
El sistema de asimilación de los datos está diseñado para minimizar los errores en las condiciones iniciales, usando varias formas de datos. La incertidumbre se toma en cuenta implícitamente (aunque de forma incompleta) a través del peso relativo de cada elemento de datos proveniente de las observaciones y el primer pronóstico del modelo. Aunque los errores en las condiciones iniciales se pueden evaluar mediante las observaciones de los satélites y otras fuentes, no es posible estimar explícitamente su impacto subsiguiente en el pronóstico numérico del tiempo. |
La incertidumbre en las condiciones iniciales se puede tomar en cuenta determinando los errores potenciales más importantes (es decir, los que crecen rápidamente) para el pronóstico subsiguiente del modelo y reducirlos a una perturbación razonable en las condiciones iniciales. (Examinaremos los métodos para determinar las perturbaciones en la sección Generación del conjunto.) |
|
Predictibilidad atmosférica |
No se puede evaluar a partir de un pronóstico determinista individual. Se puede deducir de manera incompleta a partir del grado de coherencia entre ciclos de ejecución consecutivos del modelo. |
Se puede evaluar por la razón de aumento en la dispersión de los pronósticos de los miembros del conjunto. El tamaño del conjunto y el uso de perturbaciones adecuadas en las condiciones iniciales son importantes para obtener una dispersión adecuada del conjunto y una medida de la predictibilidad. |
|
Incertidumbre de la dinámica del modelo |
Solo permite usar un único método numérico, por ejemplo, separar el flujo en senos y cosenos (método espectral). |
Se pueden usar varios métodos numéricos, por ejemplo, espectral, puntos de malla, puntos de malla con diferentes configuraciones para las variables en la malla. |
|
Incertidumbre de la física del modelo |
Solo se puede usar un conjunto de parametrizaciones físicas (por ejemplo, un determinado esquema de precipitación convectiva). |
Se pueden usar múltiples combinaciones de parametrizaciones físicas (por ejemplo, dos tipos de esquemas de precipitación convectiva para combinar sus fortalezas individuales). |
El caos y los modelos de PNT
La PNT y las condiciones iniciales
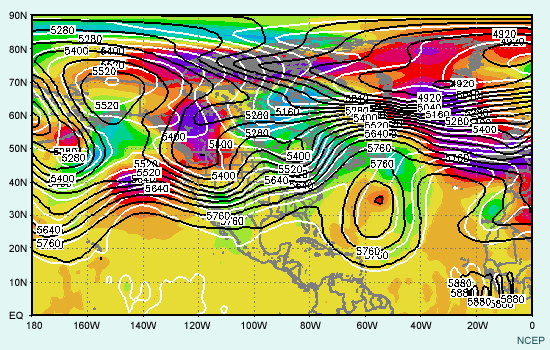
Considere animación anterior de los pronósticos de alturas en el nivel de 500 hPa del sistema global de predicción por conjuntos (Global Ensemble Forecast System) de los Centros Nacionales de Predicción Ambiental (National Centers for Environmental Prediction, o NCEP) de EE. UU., que comienza a las 1200 UTC del 22 de noviembre de 2001 y abarca 84 horas de pronóstico. La animación muestra imágenes a intervalos de pronóstico de 12 horas. Las isohipsas negras representan el pronóstico de control, que utiliza las condiciones iniciales típicas empleadas para ejecutar el modelo operativo. Las isohipsas blancas representan el pronóstico producido cuando las condiciones iniciales fueron perturbadas, es decir, cambiadas ligeramente para reflejar una duda razonable acerca de las condiciones iniciales. Los tonos de colores representan la diferencia entre el pronóstico perturbado y el de control. Observe que las perturbaciones iniciales (que se muestran en el primer fotograma) son bastante pequeñas, del orden de 10 a 20 metros en la mayoría de los lugares (amarillo, verde-amarillo y naranja). Conforme la animación avanza con el tiempo, se nota que las diferencias entre los ciclos de ejecución de control y perturbado aumentan con respecto a las numerosas características que se hallan en el estado inicial, entre las cuales se incluyen una depresión que se mueve desde el litoral atlántico de Norteamérica y otra que se desplaza hacia el sur desde el Ártico y atraviesa el noroeste de Canadá. También aparecen y se desarrollan otras características nuevas, por ejemplo, una cresta o dorsal de onda larga sobre el Pacífico este.
El caos y las condiciones atmosféricas
Si Edward Lorenz, uno de los padres de la teoría del caos, viera la animación anterior, atribuiría el desarrollo de las diferencias a la naturaleza caótica de la atmósfera. Para expresarlo con sus palabras, la atmósfera exhibe una «dependencia sensible de las «condiciones iniciales», lo cual significa que las pequeñas diferencias en el estado inicial de la atmósfera dan como resultado final grandes diferencias en el pronóstico. Sin embargo, y como descubriera Lorenz, es posible medir la sensibilidad del pronóstico a la incertidumbre en las condiciones iniciales perturbando las condiciones iniciales en un modelo de PNT.
Uso de los modelos de PNT para predecir las incertidumbres futuras: sistema de predicción por conjuntos
Hallamos evidencia adicional de la naturaleza caótica de la atmósfera en los diferentes resultados que obtenemos al ejecutar los modelos de PNT con condiciones iniciales idénticas, pero con parametrizaciones y dinámica diferentes. Los pronósticos del modelo pueden ser sensibles tanto a la estructura del modelo como a las condiciones iniciales. Cada configuración del modelo se aproxima al comportamiento real de la atmósfera de manera diferente, lo cual introduce otra fuente de incertidumbre en el pronóstico. Nunca podremos diseñar un modelo de PNT que refleje cada detalle del comportamiento de la atmósfera con una resolución infinitamente alta. Pero aún si pudiéramos crear un modelo de PNT «perfecto», su pronóstico podría eventualmente estar equivocado debido a los errores en las condiciones iniciales, aunque la degradación podría tardar más tiempo en ocurrir. Que la sensibilidad de la atmósfera dependa de las condiciones iniciales significa que las condiciones iniciales del modelo también necesitarían ser «perfectas» para que hubiera esperanza de producir un pronóstico perfecto. Por supuesto, la realidad es que nuestros sistemas de observación y asimilación nunca nos proporcionarán condiciones iniciales perfectas. Podemos, sin embargo, aplicar al proceso de pronóstico nuestro conocimiento de que la atmósfera es caótica y altamente sensible a las condiciones iniciales.
El uso estratégico de las condiciones iniciales imperfectas y/o de modelos de PNT imperfectos en un sistema de predicción por conjuntos (SPC)* permite:
- establecer una gama de resultados posibles del pronóstico,
- estimar la probabilidad para cualquier resultado individual del pronóstico, y
- determinar el resultado de pronóstico más probable (que es lo que deseamos).
La mayoría de los centros de pronóstico ya utilizan alguna versión de un sistema de predicción por conjuntos. Estos SPC operativos típicamente utilizan la incertidumbre de las condiciones iniciales como base de sus pronósticos múltiples, y algunos de ellos utilizan también la incertidumbre del modelo (estructura y dinámica imperfectas) y la incertidumbre de las condiciones de frontera. Todos estos métodos que utilizan la incertidumbre se analizan más adelante, en la sección «Generación del conjunto» de esta lección.
Las suposiciones que se hacen para construir los sistemas de predicción por conjuntos y el uso inteligente de sus salidas serán el tema de enfoque principal de esta lección. Para que usted entienda mejor la salida del SPC, presentaremos también cierta información básica y necesaria sobre estadística, probabilidad y el pronóstico probabilístico.
Si tiene interés en aprender más sobre Edward Lorenz y la teoría del caos, vea la sección opcional A fondo que sigue.
*También es muy común el uso de la sigla EPS correspondiente al inglés ensemble prediction system.
A fondo: teoría del caos
Pese a que la predicción por conjuntos es un desarrollo reciente, se basa en una teoría científica (la teoría del caos) muy conocida por décadas. Uno de los padres de la teoría del caos, el meteorólogo Edward Lorenz, descubrió que el grado de precisión numérica en las condiciones iniciales proporcionadas a un modelo de predicción numérica del tiempo (PNT) afectaba considerablemente a los resultados del pronóstico a los pocos días de tiempo de pronóstico (Lorenz 1963). Fue necesario un aumento en el poder computacional para permitir la investigación en las posibles aplicaciones de la teoría del caos al pronóstico operativo. Fue el trabajo de Tracton y Kalnay en 1993, Toth y Kalnay en 1993 y otros que finalmente dio lugar al desarrollo de la técnica de predicción por conjuntos. Esta técnica utiliza la naturaleza caótica de la atmósfera y los grandes ambientes computación masivamente paralela disponibles en la actualidad para producir modelos de PNT capaces de estimar la certeza relativa de que se produzcan determinados eventos meteorológicos específicos, tanto a corto plazo (60 horas o menos) como a mediano plazo (3 a 15 días).
El descubrimiento de los sistemas caóticos
A comienzos de los años 60, el Dr. Edward Lorenz estaba trabajando en el Instituto Tecnológico de Massachussets (MIT) con un conjunto altamente simplificado de ecuaciones diferenciales que describían los procesos convectivos de la atmósfera. El pronóstico realizado con aquellos equipos informáticos, que hoy se considerarían primitivos, producía resultados con un grado de realismo que daba esperanzas para el futuro. Un día, queriendo Lorenz extender un ciclo de ejecución particularmente interesante, en lugar de perder el tiempo comenzándolo de nuevo, introdujo manualmente los datos en algún punto intermedio del ciclo de ejecución y continuó ejecutando el modelo. Para su sorpresa, encontró que poco después de haber reiniciado el modelo a partir de ese punto intermedio, el pronóstico había divergido del primer resultado hasta hacerse totalmente irreconocible, a pesar de haber comenzado con las mismas condiciones. Pero, ¿eran de veras las mismas?
Resulta que los datos de la salida que utilizó para recomenzar este modelo atmosférico simple habían sido redondeados a 3 dígitos significativos, mientras que los cálculos se habían hecho con 6 dígitos, produciendo un error de cerca del 1 %, un margen de error que el Dr. Lorenz nunca hubiera considerado significativo. Sin embargo, este experimento involuntario y su resultado inesperado mostraron que los pequeños errores en ese sistema particular (y en otros como ése) tienen gran importancia. A partir de este descubrimiento inicial, el Dr. Lorenz demostró que la atmósfera puede exhibir lo que parece ser un comportamiento caótico, incluyendo un alto grado de sensibilidad a las condiciones iniciales con las cuales se comienza un pronóstico. Sin embargo, después de un estudio, se demostró que en realidad los pronósticos que comienzan con diferentes condiciones iniciales pueden favorecer ciertos patrones, regiones o regímenes.
El sistema de Lorenz
Las implicaciones de la dependencia sensible a las condiciones iniciales se pueden fácilmente observar en el sistema de Lorenz de tres ecuaciones diferenciales que representan la viscosidad atmosférica, la rotación de la tierra y los gradientes horizontales y verticales de la temperatura (aunque para propósitos de demostración podríamos utilizar muchas combinaciones de variables). Las tres imágenes que siguen muestran la integración en intervalos de este sistema de ecuaciones con condiciones iniciales ligeramente diferentes (nuestra ilustración se basa en la salida real de un sistema de Lorenz). El gráfico muestra las integraciones en tres momentos a intervalos uniformes, denotados por T+2, T+4 y T+6, que representan un total de cerca de 1200 pasos de tiempo. Los resultados del pronóstico de control están en rojo, los resultados del pronóstico perturbado están en azul.
Mientras los valores X, Y y Z suelen representar coordenadas espaciales, en el sistema de Lorenz representan el estado del sistema. Aquí, X, Y y Z son, respectivamente, la intensidad del movimiento convectivo, la diferencia de temperatura entre las corrientes ascendentes y descendentes y la distorsión del perfil vertical de temperatura lineal. Si X e Y son del mismo signo, el fluido cálido asciende y el fluido frío desciende y si Z es positivo, los gradientes de temperatura más intensos ocurren cerca de los límites del dominio.
Note que es prácticamente imposible distinguir los puntos de partida de los dos pronósticos (los pequeños cuadrados rojo y azul en el diagrama T+2). De hecho, la diferencia en el valor inicial de Z es de más o menos el 0,1 %, un valor representativo de los errores instrumentales que suelen producirse en las mediciones atmosféricas. En T+2, los pronósticos siguen siendo casi idénticos (estrellas roja y azul). Sin embargo, pese a que en T+4 los pronósticos siguen todavía la misma trayectoria aproximada y están comenzando a emerger dos regímenes comunes (representados por los dos lazos), el pronóstico del control está atrasado y comienza a separarse del pronóstico perturbado. En T+6, los dos pronósticos divergen significativamente y ya están en regímenes diferentes.
T + 2
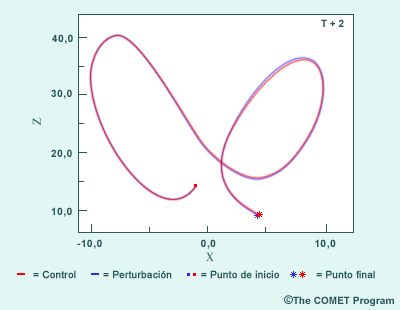
T + 4
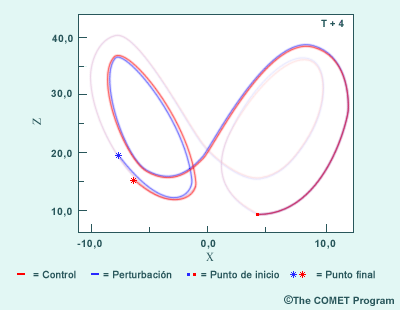
T + 6
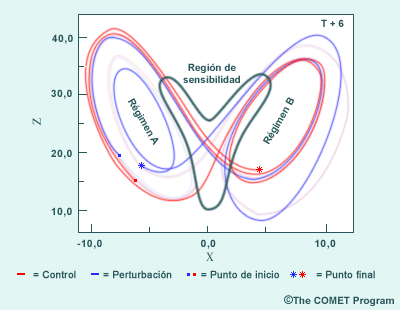
Conviene destacar algunos aspectos interesantes de este sistema. Observe que:
- Los pronósticos comienzan a divergir después de un tiempo muy corto.
- Los pronósticos parecen preferir dos regiones generales o «regímenes» en la figura (rotulados régimen A y régimen B).
- Las áreas próximas a la intersección de los regímenes parecen ser más sensibles a las perturbaciones que las otras áreas. Estas áreas se muestran encerradas en una línea verde en la última figura. Cuando una trayectoria entra en esta región, la dirección que se seguirá al final se vuelve más incierta.
- No importa dónde comencemos, todas las trayectorias pronosticadas eventualmente entran en el área de sensibilidad, donde pequeños cambios en la posición originarán diferencias importantes en el pronóstico.
El sistema de Lorenz es un sistema con solo tres grados de libertad, y aún así es impredictible a lo largo del tiempo. Por otra parte, la atmósfera real considerada como un sistema caótico tiene muchos grados de libertad. Sin embargo, no todo está perdido. El hecho de que un sistema sea caótico no significa que sea aleatorio. Por ejemplo, podemos ver en el gráfico que el sistema de Lorenz tiene dos regímenes distintos (o «atractores», para usar la terminología propia de la teoría del caos). Las trayectorias pronosticadas no se apartan de estos regímenes. Además, dentro de los regímenes individuales, la trayectoria es relativamente predictible, hasta entrar en la región de sensibilidad en el límite entre los dos regímenes.
A partir de unas observaciones generales, podemos ver que la atmósfera tiene muchos aspectos similares al sistema simplificado de Lorenz. Sabemos que:
- La evolución del estado atmosférico es limitada por la actividad solar, que varía estacionalmente, la geometría de la Tierra, la localización de las masas continentales y oceánicas y otros aspectos fijos de los límites de la atmósfera superior e inferior.
- La atmósfera sigue ciertos patrones, lo cual significa que tiene algunos modos de variabilidad preferidos.
- Y lo más importante: el comportamiento de la atmósfera es altamente sensible a las condiciones iniciales.
Generación del conjunto
Existen diferentes métodos para crear los conjuntos de PNT, pero en todos ellos habrá elementos de incertidumbre en los datos o en el mismo modelo de PNT. Cada pronóstico individual dentro de un ciclo de ejecución por conjuntos (que se denomina miembro del conjunto) utiliza uno o más aspectos de esta incertidumbre. Entre los posibles métodos para capturar las incertidumbres inherentes al pronóstico se incluyen los siguientes:
- La perturbación de las condiciones iniciales usadas en los pronósticos del modelo.
- La perturbación del modelo de PNT, a través de cambios en:
- la formulación dinámica (p. ej.: diferentes tipos de coordenadas verticales);
- los métodos numéricos (p. ej.: diferentes métodos, como modelos de malla o espectrales);
- las parametrizaciones físicas (p. ej.: diferentes parametrizaciones de la precipitación convectiva o de la precipitación a escala de malla);
- la resolución horizontal y/o vertical.
- Las perturbaciones en las condiciones de frontera:
- condiciones de frontera superficial (p. ej.: temperatura de la superficie del mar o humedad del suelo;
- condiciones de frontera lateral (se encuentran en los modelos regionales, p. ej.: las condiciones cambiantes proporcionadas por la predicción por conjuntos de un dominio mayor).
Exploraremos cada uno de estos temas en la próxima sección.
Fuentes de perturbación
Incertidumbre en las condiciones iniciales de los conjuntos
Está claro que no se conoce perfectamente el estado atmosférico en un determinado momento; los errores inherentes de los instrumentos usados en la red de recopilación de datos garantizan la veracidad de esta afirmación. También contribuyen a la incertidumbre de las condiciones iniciales los siguientes aspectos:
- observaciones incompletas de la atmósfera (obviamente, no se observan todas las variables en todos los lugares todo el tiempo);
- sistemas imperfectos de asimilación de datos.
Por tanto, un pronóstico generado a partir de unas condiciones atmosféricas iniciales debe contener errores y con el tiempo algunos de estos errores crecen hasta dominar el pronóstico.
Un análisis del estado inicial de la atmósfera por parte de un modelo de PNT puede incorporar un número infinito de valores dentro del rango de incertidumbre y esto, en teoría, ¡daría lugar a un número infinito de posibles evoluciones del pronóstico! En el año 2004, el sistema informático de NCEP no podía ejecutar más de una docena de simulaciones de la atmósfera por ciclo de pronóstico; el Centro Europeo de Predicción a Plazo Medio (CEPPM/ECMWF) solo consigue ejecutar 50 simulaciones por día.
Dada la disponibilidad limitada de recursos computacionales, el problema se convierte en:
- definir un rango razonable de incertidumbre en las condiciones iniciales, y luego
- determinar qué incertidumbres en ese rango crearán una serie de pronósticos por conjuntos con el rango apropiado de soluciones posibles en el intervalo de tiempo de interés.
Rango de incertidumbre
El rango de incertidumbre en las condiciones iniciales depende del sistema de asimilación de datos empleado. Cada sistema de asimilación de datos se ve afectado por los errores característicos de las observaciones incorporadas en el análisis y del pronóstico a corto plazo del modelo, que típicamente se utiliza como base o «primera aproximación» y se ajusta luego con nuevas observaciones. (La lección Comprensión de los sistemas de asimilación, versión 2 explica en detalle cómo funcionan los sistemas de asimilación de datos). Las observaciones y el pronóstico a corto plazo se combinan para reducir al mínimo el error en las condiciones iniciales del dominio del pronóstico. Este proceso minimiza, pero no elimina por completo, las incertidumbres en las condiciones iniciales. Las diferencias en las condiciones iniciales usadas por cada uno de los pronósticos en un SPC, tomadas como un todo, deberían abarcar el rango de incertidumbre que queda (el error minimizado) en las condiciones iniciales.
Cada pronóstico individuales dentro de un SPC se conoce como miembro del conjunto. En el caso de los sistemas de predicción por conjuntos que usan la incertidumbre en las condiciones iniciales para crear un pronóstico, la ejecución del miembro del conjunto a partir del análisis sin cambios (interpolado hacia la resolución del sistema de conjunto) se conoce como control del conjunto. Los miembros que se ejecutan a partir de análisis que han sido cambiados para reflejar las incertidumbres en las condiciones iniciales se conocen como perturbaciones del conjunto.
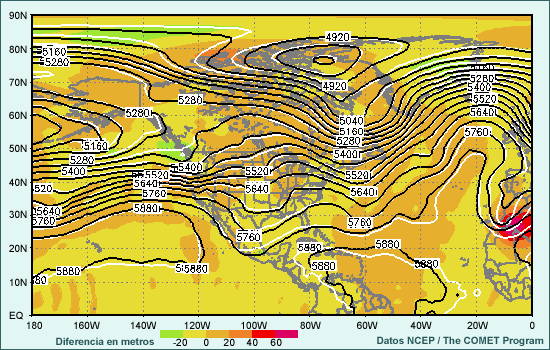
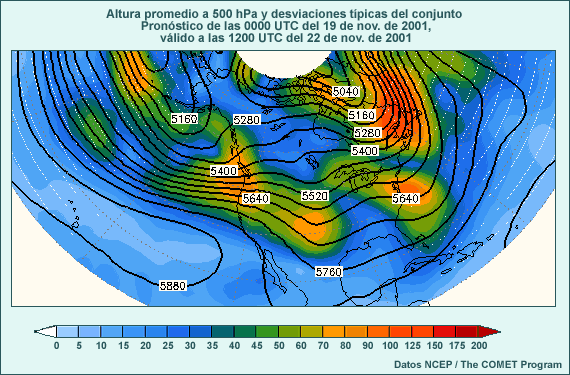
El mapa siguiente muestra un ejemplo (obtenido del sistemas de predicción por conjuntos del NCEP) de la diferencia entre las condiciones iniciales del control y uno de los miembros perturbados del conjunto para el campo de alturas de 500 hPa en el hemisferio norte. Las isohipsas negras representan el control del conjunto, las isohipsas blancas, la perturbación del conjunto y los distintos tonos de colores la diferencia entre los dos, todo dado en metros.
Incertidumbres en la formulación del modelo
Una fuente adicional de incertidumbre en los pronósticos es la formulación imperfecta del modelo, que incluye las contribuciones de:
- la formulación dinámica (incluyendo errores numéricos resultantes del truncamiento espectral y de malla), y
- la formulación de la parametrización física a escala de malla y a una escala inferior a la malla.
Las imperfecciones en la formulación del modelo también contribuyen a los errores y sesgos sistemáticos que vemos en todos los modelos operativos. Por ejemplo, es probable que el sesgo hacia el frío que se suele observar en los pronósticos del modelo GFS para la troposfera baja en invierno sobre el territorio continental de los EE. UU. sea consecuencia de una imperfección en la formulación del modelo GFS operativo. El impacto de los sesgos y los errores sistemáticos en un pronóstico en particular depende del régimen de flujo y de las particularidades de las condiciones de frontera, entre otros factores.
Hace ya muchos años que se reconoce la existencia de las incertidumbres en los modelos de PNT en el ámbito del pronóstico operativo, y a veces esto nos obliga a escoger el «modelo del día», es decir, el modelo de PNT que está manejando mejor la evolución atmosférica. Sin embargo, la elección del «modelo del día» es subjetiva y puede no reflejar una comprensión adecuada de qué aspecto del modelo elegido produce lo que se juzga como un mejor pronóstico, especialmente cuando el desempeño promediado en el tiempo de los modelos considerados es esencialmente equivalente.
Cómo «perturbar» el modelo de pronóstico
Una forma de tomar en consideración las incertidumbres inherentes a la formulación del modelo consiste en «perturbar» el modelo mismo. Tales perturbaciones pueden incorporar aspectos de la formulación dinámica (por ejemplo, cambiar el tipo de coordenada vertical de sigma a eta), del cálculo numérico (por ejemplo, modelo de malla o espectral, simulación de errores numéricos aleatorios como resultado del truncamiento de la malla o del número de onda), o de la parametrización física (por ejemplo, el esquema de parametrización de la convección de Kain-Fritsch o de Betts-Miller-Janjic para simular las perturbaciones del forzamiento causado por los procesos físicos a una escala inferior a la malla).
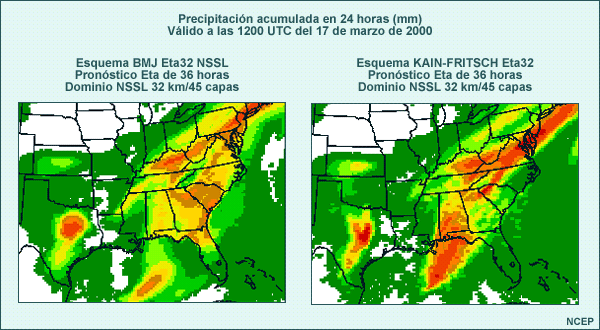
El gráfico siguiente muestra un ejemplo del efecto de una perturbación introducida en la parametrización física de un pronóstico de precipitación de 24 horas del modelo Eta (en el intervalo de 12 a 36 horas de pronóstico). Los modelos se diferencian solamente por sus parametrizaciones convectivas. El pronóstico del esquema operacional BMJ está a la izquierda y el del esquema KF a la derecha. Observe también que esta situación ocurrió durante la estación fría (marzo de 2000).
Observe las semejanzas y las diferencias entre los dos pronósticos:
- Ambos pronósticos producen máximos de precipitación sobre los estados de Texas, Kansas, al este de Kentucky y Tenesí, sobre el norte de Georgia y al noroeste de la Carolina del Sur.
- En el pronóstico de Kain-Fritsch (gráfico de la derecha), no existe el máximo de precipitación que abarca la costa de Carolina del Sur y Georgia y el norte de Florida, ni la zona en el oeste de Misisipí y sudeste de Arkansas.
- La banda de fuerte precipitación en los estados del Atlántico medio está desplazada hacia el sudeste en el pronóstico de Kain-Fritsch.
Los diferentes esquemas convectivos no solo influyen cuantitativamente en la cantidad de precipitación, sino también en su evolución dinámica, porque los esquemas tienen diferentes disparadores y distintos perfiles de calentamiento vertical a los cuales responde la dinámica. A continuación se muestra un sondeo de ambos esquemas para una localidad en el noroeste de Florida, cerca de la zona donde hay una gran diferencia en los pronósticos de precipitación.
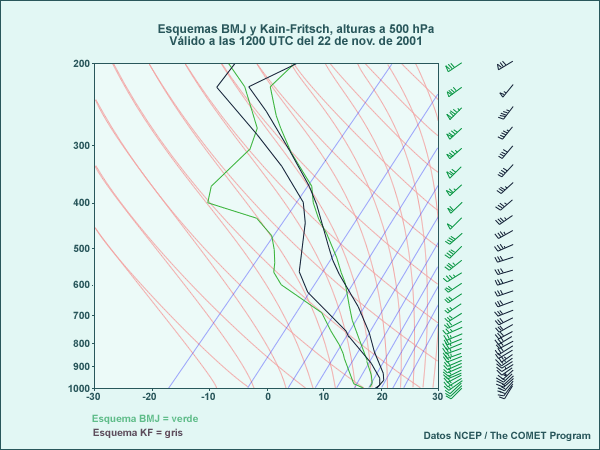
Observe la diferencia en los perfiles de viento, temperatura y humedad, particularmente entre 500 hPa y la tropopausa (cerca de 250 hPa). Los vientos a entre 400 y 300 hPa son de 30 a 40 nudos más intensos con el esquema BMJ de lo que es el caso con el esquema KF. El esquema BMJ crea también condiciones más cálidas y más secas en la troposfera media y alta. Tales respuestas dinámicas pueden generar diferencias en ciclogénesis y frontogénesis, y en la posición y la velocidad de desplazamiento de los sistemas sinópticos.
Incertidumbre del valor de frontera
Una tercera categoría general de la generación de conjuntos mediante la evaluación del grado de incertidumbre surge de la asignación de valores a las variables significativas en las fronteras inferior y laterales. Los valores de frontera inferior que se pueden perturbar son:
- la temperatura superficial del mar (TSM)
- la humedad del suelo
- las condiciones de frontera preestablecidas (p. ej.: el tipo de vegetación o de suelo)
A veces se utilizan las perturbaciones de la humedad del suelo o de la temperatura de la superficie del mar para los conjuntos climáticos. Por ejemplo, el Centro de Predicción Climática (CPC) de los EE. UU. usa un conjunto de pronósticos de la TSM para forzar una versión climática del modelo GFS de NCEP para varios meses. La predicción por conjuntos resultante se analiza luego para su uso en los pronósticos estacionales del CPC. En la actualidad, los conjuntos globales operativos de NCEP no hacen uso de condiciones de frontera perturbadas de este tipo para crear los miembros del conjunto.
Las fronteras laterales solo se pueden perturbar en los modelos regionales, que tienen como entrada los valores de fronteras laterales de un modelo de malla o espectral de menor resolución. Una configuración posible para un sistema regional de predicción por conjuntos podría incluir condiciones de frontera laterales a partir de un conjunto de pronósticos globales. La predicción por conjuntos a corto plazo (Short-Range Ensemble Forecast, o SREF) del NCEP, por ejemplo, utiliza los conjuntos globales para las perturbaciones de fronteras laterales, así como sus propias perturbaciones generadas a nivel regional.
Implementaciones
CEPPM/ECMWF: cálculo de vectores singulares
CEPPM/ECMWF: cálculo de vectores singulares
En el Centro Europeo de Predicción a Plazo Medio (CEPPM/ECMWF) se utiliza el método de vectores singulares para perturbar las condiciones iniciales. En la versión simplificada del modelo de pronóstico del CEPPM/ECMWF a corto plazo (48 horas) se utilizan métodos estadísticos para calcular las direcciones o «vectores» en los que las diferencias del pronóstico crecerán más rápidamente con el tiempo. A partir de dichos vectores de crecimiento más rápido, el sistema de predicción por conjuntos retrocede hasta el tiempo inicial para obtener la estructura de la incertidumbre de las condiciones iniciales directamente relacionada con los «vectores» de crecimiento rápido. Luego el tamaño de estos vectores o perturbaciones se ajusta a los errores de observación esperados y los de la primera aproximación encontrados en el sistema de asimilación de datos del modelo. Finalmente, se suman a las condiciones iniciales de una versión de resolución más baja del modelo operacional de PNT del CEPPM/ECMWF. Encontrará más detalles sobre el uso del método de vectores singulares para determinar los errores más importantes de las condiciones iniciales que afectan a la evolución del pronóstico de mediano plazo del CEPPM/ECMWF en el artículo Chaos and weather prediction, enero de 2000, (El caos y la predicción del tiempo) que está disponible en inglés en el sitio web del CEPPM/ECMWF.
NCEP: cálculo de las perturbaciones mediante un ciclo de «incubación»
El término «ciclo de incubación» se refiere al hecho de que este método «incuba» o genera las perturbaciones de las condiciones iniciales que dan lugar a los mejores pronósticos por conjuntos. Para iniciar un ciclo de incubación, se añaden perturbaciones aleatorias a las condiciones iniciales de análisis del modelo. Se ejecutan entonces un pronóstico de control y otro perturbado para un plazo de pronóstico corto (generalmente de 24 a 48 horas). Luego los pronósticos de control y perturbado se diferencian para llegar a una perturbación tridimensional. Finalmente, esta perturbación se reduce a un tamaño que refleje las incertidumbres en las observaciones y en la primera aproximación usada en el sistema de asimilación de datos. Estas nuevas perturbaciones se aplican entonces a un nuevo análisis proveniente del nuevo período de pronóstico y el ciclo «de incubación» se repite. Después de repetir el ciclo por algunos días, las diferencias entre el control y el pronóstico se estabilizan y de este modo se incuba con éxito la perturbación de crecimiento más rápido. Después de ajustarla a escala, la perturbación se suma y se resta del control para crear un par «incubado» de perturbaciones de condiciones iniciales. Los pares incubados se utilizan para centrar las condiciones iniciales en las condiciones iniciales de control, que se consideran como el mejor análisis posible. Este gráfico muestra cómo se determina una única perturbación en el ciclo de incubación.
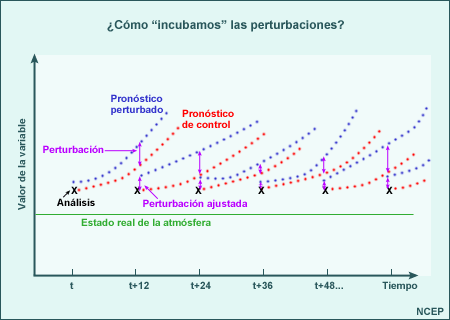
En un sistema de predicción por conjuntos (SPC), el número de pares incubados depende de la capacidad computacional disponible para la predicción por conjuntos. Observe que el uso de los ciclos de incubación para generar perturbaciones en las condiciones iniciales se basa en las siguientes suposiciones básicas:
- los aspectos más importantes de la incertidumbre en la condiciones iniciales aparecerán y se volverán dominantes muy temprano en el período del pronóstico; y
- continuarán siendo importantes en el intervalo de interés del pronóstico.
Configuración del SPC de mediano plazo del NCEP; comparación con el método del CEPPM/ECMWF
En septiembre de 2004, la configuración del SPC de mediano plazo del NCEP utilizaba cinco ciclos de incubación para crear 10 perturbaciones (5 positivas y 5 negativas). Los ciclos se realizaban a intervalos de 6 horas y las diferencias entre el control y la perturbación se calculaban cada 24 horas de pronóstico y se ajustaban al tamaño del error del análisis.
Resulta que los métodos de vectores singulares y de ciclo de incubación producen resultados más o menos equivalentes. Las ventajas del ciclo de incubación son que es un método relativamente poco costoso de ejecutar y mantener y que toma en cuenta los procesos no lineales del modelo al determinar las perturbaciones.
Formulación del modelo
En marzo de 2004, la predicción por conjuntos a mediano plazo (Medium-Range Ensemble Forecast, o MREF) del NCEP no utilizaba los modelos perturbados para producir pronósticos por conjuntos, mientras que la predicción por conjuntos a corto plazo (Short-Range Ensemble Forecast, o SREF) regional utilizaba dos modelos, uno de los cuales se ejecuta con dos parametrizaciones convectivas diferentes.
CMC: observaciones perturbadas en múltiples ciclos de análisis
En el Servicio Meteorológico de Canadá (Meteorological Service of Canada, o MSC), el sistema de predicción por conjuntos (SPC) utiliza un conjunto de ciclos de asimilación de datos que realizan análisis independientes. Cada ciclo de asimilación de datos emplea las observaciones perturbadas de manera diferente y una base o primera aproximación también perturbada de manera diferente. Las perturbaciones de las observaciones y de la aproximación inicial se obtienen aleatoriamente a partir del rango de error esperado en las observaciones y en el modelo, respectivamente, usando un método de Monte Carlo. Se supone que donde se dispone de muchas observaciones de buena calidad, la dispersión del conjunto de análisis será relativamente pequeña. Por otra parte, donde no se dispone de muchas observaciones exactas y donde la atmósfera es dinámicamente inestable, la dispersión del conjunto de análisis será bastante grande. El conjunto de análisis proporciona las condiciones iniciales para los miembros del conjunto del SPC.
Es posible usar el llamado filtro de Kalman para conjuntos (Ensemble Kalman Filter, o EnKF) para proveer al sistema de asimilación de datos y al SPC una estructura tridimensional de los «errores del día» para los campos de aproximación inicial y de análisis. El EnKF permite variar la estructura del error de análisis y de aproximación inicial, basándose en el régimen de flujo actual. El uso del EnKF da como resultado un vínculo directo entre el sistema de asimilación de datos y el sistema de predicción por conjuntos.
En la primera versión del sistema MSC-EPS, que se implementó en febrero de 1998, el sistema de asimilación de datos no utilizaba un filtro EnKF para proporcionar información sobre la incertidumbre de la aproximación inicial. Sin embargo, en agosto de 2004 se iniciaron pruebas en paralelo con un SPC que obtiene su conjunto de condiciones iniciales de un filtro EnKF. La implementación operativa se programó para el otoño de 2004.
Conceptos estadísticos
En esta sección se describen brevemente varios conceptos básicos de estadística que resultan necesarios para entender y utilizar los productos de un sistema predicción por conjuntos (SPC), incluídas las medidas estadísticas y sus aplicaciones en los SPC. Los sistemas de predicción por conjuntos utilizan todos estos conceptos para generar resultados útiles para generar pronósticos y para evaluar y mejorar el sistema de conjuntos. Considere, por ejemplo, los productos siguientes.
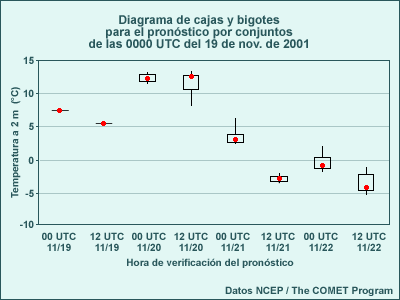
Tiempo de verificación del pronóstico
Con el fin de utilizar estos productos de la mejor forma posible, se deben tener muy claros los conceptos de media estadística, desviación típica (o estándar), cuartiles y mediana. Es también importante comprender estos y otros conceptos estadísticos para poder interpretar los productos de verificación de los sistemas de predicción por conjuntos (o de cualquier modelo de PNT). Si estos conceptos le son familiares, puede leer por encima o incluso saltar las primeras partes de esta sección. Sin embargo, recomendamos leer los tres apartados finales —«Uso de las funciones de densidad de probabilidad (FDP)», «Aplicación de los datos» y «Ejercicios»—, ya que muestran cómo dichos conceptos se aplican a las predicciones por conjuntos.
Distribuciones de probabilidad
Distribuciones teóricas de probabilidad
Para generar información estadística, normalmente se trabaja con una muestra finita de datos obtenidos de un conjunto grande (o infinito) de datos para el cual no sería práctico o posible obtener todos los datos. Por ejemplo, el Centro Nacional de Datos Climáticos (National Climatic Data Center, o NCDC) de EE. UU. utiliza los datos de las tres últimas décadas para sus cálculos estadísticos, suponiendo que son representativos del clima a largo plazo.
Una distribución de probabilidad representa la frecuencia de ocurrencia de valores o rangos de valores específicos en una muestra particular de datos. Si la muestra es representativa y suficientemente grande, la distribución de probabilidad se puede utilizar para estimar las características de todo el conjunto de datos. Por ejemplo, el gráfico que aparece a continuación representa una distribución de probabilidad hipotética de las temperaturas máximas pronosticadas por un SPC. El gráfico muestra el porcentaje de los pronósticos hechos para cada valor de temperatura (quizás para varios puntos de malla en determinada región, de modo que la muestra puede ser bastante grande). Cabe preguntarse en qué medida es representativa esta distribución de todos los resultados posibles, dadas las mismas condiciones iniciales. ¿Podemos suponer que la probabilidad de que la temperatura máxima sea igual o mayor que 32 °C excede el 87 %, como indica la predicción por conjuntos?
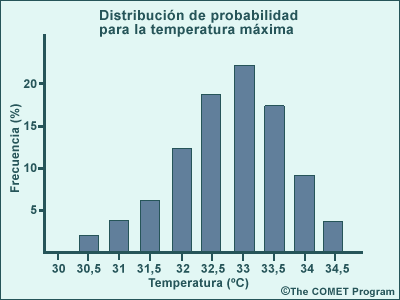
Una distribución de probabilidad puede exhibir varias formas generales según la distribución teórica en la cual se basa. La distribución de probabilidades ilustrada en la gráfica anterior —la cual presenta un pico de frecuencias central y «colas» con muchos menos valores en los extremos— se aproxima a una distribución normal (este concepto se explica en la próxima página). Cuando trabajamos con distribuciones de probabilidad y aplicamos métodos estadísticos, hacemos suposiciones sobre la distribución teórica a la que se ajustan mejor, incluso cuando presentan formas mucho menos evidentes. Normalmente, elegimos la distribución teórica de acuerdo con las características de los procesos físicos medidos por los datos. Además, los datos de la muestra se pueden someter a prueba para determinar si se ajustan adecuadamente a la distribución teórica elegida.
Por lo general, cuanto más grande sea el conjunto de datos de la muestra, tanto más podemos confiar en que la distribución teórica elegida se ajuste a la muestra y que la distribución de probabilidades de la muestra constituya una buena aproximación del conjunto de datos más grande. Obviamente, si la hipótesis de que la muestra de datos es representativa del conjunto de datos más grande del cual proviene es FALSA, las estadísticas calculadas a partir de ella no serán representativas de dicho conjunto de datos más grande.
Considere ahora un sistema de predicción por conjunto. De forma análoga a la gráfica anterior, el sistema genera una muestra de pronósticos posibles a partir de una población de posibilidades de pronóstico mucho más grande. A partir de dicha muestra podemos inferir la mayor o menor «centralidad» (tendencia al medio) y «variabilidad», así como la «forma» de la distribución de la población que comprende todos los posibles resultados de pronóstico (cada una de estas características se describe en las secciones que siguen). No obstante, todavía tenemos que considerar las salvedades hechas anteriormente: es posible que el conjunto de datos del pronóstico por conjuntos (es decir, la muestra de datos) no sea representativa de todos los posibles resultados de pronóstico. Trataremos este tema en varias ocasiones a lo largo de la lección, especialmente en las secciones sobre «Productos» y «Verificación».
La función de densidad de probabilidad (FDP)
(Nota: en el resto de esta lección se usarán indistintamente los términos distribución de probabilidad y FDP.)
Para describir sucintamente la distribución de probabilidad de una muestra de datos obtenida de un conjunto grande de datos, utilizamos lo que se conoce como función de densidad de probabilidad, o FDP, en la cual el eje x representa los valores posibles para los datos y el eje y la probabilidad de que ese valor ocurra, de acuerdo con la muestra de datos (vea el ejemplo más adelante). La FDP tiene una forma característica, una posición característica de su «centro» y una variabilidad o dispersión característica de los valores.
Algunos datos pueden aceptar solo valores discretos, como la ocurrencia o no ocurrencia de precipitación mensurable en un intervalo de tiempo. Entre las posibles distribuciones teóricas de probabilidad discretas existen la distribución binomial, la distribución geométrica y la distribución de Poisson. Sin embargo, ciertos datos pueden aceptar cualquier valor numérico real dentro de cierto intervalo finito o infinito, y estos se describen utilizando distribuciones teóricas de probabilidad continuas, por ejemplo la distribución gaussiana o «normal » y las distribuciones beta, gamma o de valores extremos.
En el resto de esta subsección describiremos la distribución normal teórica, pero podrá encontrar detalles sobre otras distribuciones teóricas de uso común en la sección A fondo que aparece más adelante. En los tres apartados siguientes describiremos algunos parámetros empleados para describir las distribuciones de probabilidad.
La distribución normal (gaussiana)
La distribución normal o gaussiana es la forma de distribución más utilizada para describir estadísticamente los datos. En estas distribuciones, los valores próximos a la media se observan con más frecuencia y los valores extremos son bastante raros (creando la familiar curva normal o de Gauss, que tiene forma de campana). Dos parámetros estadísticos, la media y la desviación típica (una medida de la distancia desde la media, que se discutirá en detalle más adelante), describen por completo los datos de distribución normal. Otro aspecto conveniente de la distribución normal es que incluso cuando una muestra de datos no se distribuye normalmente, las medias de todas las muestras de datos obtenidas de la población sí tienen una distribución normal. La gráfica siguiente muestra una distribución normal con una media de 0,0 y una desviación típica de 1,0. La anchura de cada barra corresponde a 1 desviación típica y muestra la probabilidad de que un valor se halle entre 0 y ±1, ±1 y ±2, etc., en las desviaciones típicas alejadas de la media. La probabilidad de los valores dentro de cada barra se indica en forma numérica. (Observe que los valores más allá de ±3 son demasiado pequeños como para detectarse por medio de las barras, pero existe una probabilidad de 0,0013 de que ocurran. Observe además que la integración en el rango total de la curva normal (± infinito) debe ser igual a 1,0; es decir, la suma de todas las probabilidades debe ser 100 %.
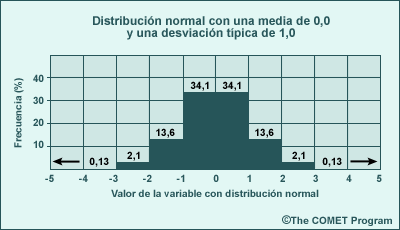
La distribución normal se aplica a muestras grandes de datos meteorológicos sin límites superiores e inferiores cercanos y que tienden a presentar un valor medio, como las temperaturas o las alturas de una superficie de presión constante. A continuación se muestra un diagrama de frecuencias (es decir, un histograma) de la altura al nivel de 500 hPa a intervalos de 50 metros, a partir del reanálisis del NCEP en 125°O de longitud y 42.5°N de latitud, para todo el mes de noviembre entre los años 1979 y 1995, comparada con una distribución normal teórica con la misma media y desviación típica. Observe que el ajuste entre las dos distribuciones es muy bueno.
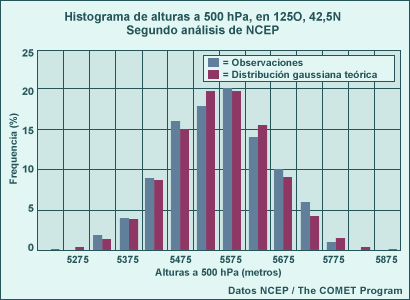
Normalmente, en la estadística de las predicciones por conjuntos se supone una distribución normal. A veces, sin embargo, los datos de la predicción por conjuntos no tienen una distribución normal, como es el caso, por ejemplo, cuando es preciso pronosticar dos o más regímenes diferentes, lo cual significa que hay dos o más pronósticos con alta frecuencia. En tales casos, los resultados estadísticos obtenidos a partir de la muestra de los datos del conjunto pueden no ser representativos de la población de pronósticos y pueden, de hecho, causar equivocaciones. Hablaremos de esto más adelante, en la sección Aplicación de datos.
A los fines de esta lección, es suficiente entender las características de una distribución normal. Sin embargo, existen muchas otras distribuciones. Encontrará una breve descripción de otras distribuciones utilizadas en meteorología en la sección opcional A fondo que sigue. Para obtener información detallada sobre las distribuciones teóricas de probabilidad, sugerimos el libro de estadística de Wilks (1995), mencionado en la bibliografía.
A fondo: otras distribuciones
-
Distribución binomial (sí/no)
Para que la distribución binomial sea una suposición válida, solo pueden ser posibles dos resultados (por ejemplo, lluvia o no lluvia, temperatura mínima mayor que 0 °C o igual o menor que 0 °C) y el resultado de cada ensayo debe ser independiente de los otros. La FDP para esta distribución es la probabilidad de que un número de eventos ocurra en un número específico de ensayos independientes. Usando el diagrama que sigue, por ejemplo, si se determina que la probabilidad de lluvia para el 13 de abril es del 30 % (0,3), la FDP de los días 13 de abril lluviosos en un intervalo de 100 años está dada por la curva celeste (que abarca de 18 a 42, siendo 30 la probabilidad máxima). No podemos usar este método para dar una FDP del número de días lluviosos que podría ocurrir en 100 días consecutivos, puesto que la ocurrencia de lluvia en un día dado aumenta la probabilidad de ocurrencia para el día siguiente. Para describir tales distribuciones de probabilidad se utilizan métodos más generales, que están fuera del alcance de esta lección.
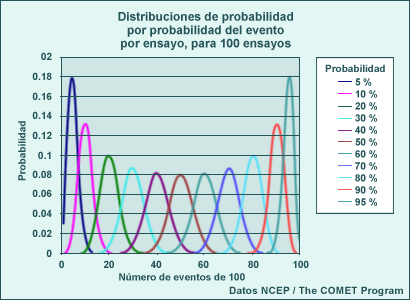
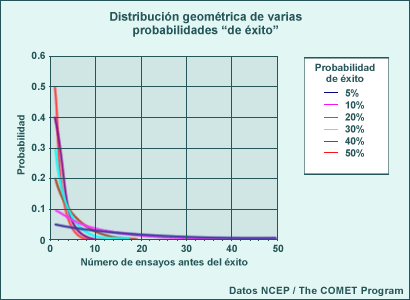
- Distribución geométrica
La distribución geométrica está relacionada con la distribución binomial, pero da la probabilidad de ocurrencia o de «éxito» de un evento (por ejemplo, de que lloverá) después de un número específico de «fallas» o eventos contrarios, típicamente en un intervalo de tiempo específico. La probabilidad de ocurrencia de un evento no debe cambiar de un ensayo a otro. Un ejemplo en un régimen meteorológico específico es la probabilidad que el régimen cambie en N días.
-
Distribución de Poisson
Las distribuciones de Poisson describen la probabilidad de que cierto número de eventos ocurra en determinado período cuando la probabilidad de ocurrencia depende solamente de la duración del período. Esto suele aplicarse a eventos extremos, como el número de huracanes o tornados que ocurren anualmente. La razón media de ocurrencia es el único parámetro de la distribución.
La gráfica siguiente muestra un ejemplo de una distribución de Poisson para los días con temperaturas máximas por debajo de 0 °F (-17,8 °C) en Minneapolis, Minesota, EE. UU., para los 30 inviernos entre 1960-61 y 1989-90. La media es de cerca de 4,1 días. La distribución de Poisson teórica se da en azul claro y la distribución real en azul oscuro.
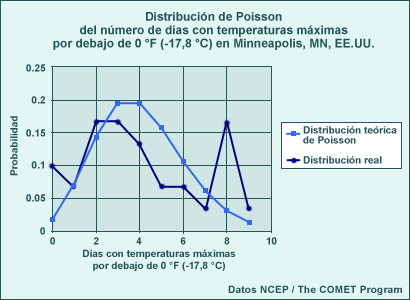
- Distribuciones Gamma (sesgadas o con límite mínimo)
Se han desarrollado distribuciones teóricas denominadas distribuciones gamma para las distribuciones no normales de fenómenos meteorológicos tales como la precipitación o velocidad del viento, donde hay un límite a la izquierda de la FDP que está cerca de los valores medios. Las distribuciones gamma están sesgadas a la derecha y utilizan dos parámetros para controlar la forma de la distribución y la cantidad de probabilidad que se ubica en el extremo derecho de la distribución.
-
Distribuciones Beta (con límites mínimo y máximo)
Para las distribuciones beta, existen fronteras físicas mínimas y máximas. Tales distribuciones teóricas son útiles, por ejemplo, para la nubosidad (que varía de 0,0 a 1,0) y la humedad relativa (que varía del 0 al 100 %). Las distribuciones beta pueden tener probabilidades máximas en los extremos o en el centro del rango de las variables, con un alto grado de flexibilidad en la forma según los valores de sus parámetros. Los parámetros se eligen para obtener el mejor ajuste con la muestra de datos que se está utilizando. Por ejemplo, si los datos fueran la nubosidad en Phoenix, Arizona, podríamos esperar un mejor ajuste con parámetros similares a los usados para la línea violeta en la gráfica siguiente (es decir, p=0,5 y q=2,0), que muestra una alta probabilidad para valores bajos y probabilidades decrecientes y bajas para valores altos de nubosidad.
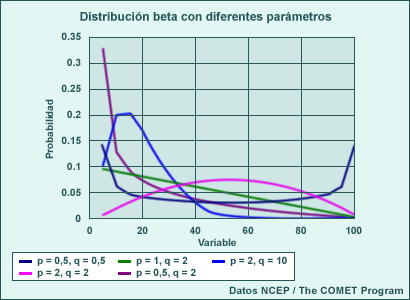
- Distribuciones de valores extremos
Las distribuciones teóricas de valores extremos se utilizan para estimar la probabilidad de ocurrencia de un valor extremo en particular. Tales distribuciones se pueden utilizar para determinar la probabilidad de observar una temperatura muy alta (por ejemplo: 38 °C) en algún mes determinado o una precipitación máxima (por ejemplo: 60 mm) en un año determinado.
Probabilidad conjunta
A menudo, nos interesa saber la probabilidad de que se produzca más de un evento al mismo tiempo. Un buen ejemplo para la estación fría es el tipo de la precipitación: ¿cuál es la probabilidad de que se produzcan temperaturas bajo cero y lluvia?
Tales probabilidades se denominan probabilidades conjuntas. En términos geométricos, si representáramos las probabilidades para dos eventos como porciones de una unidad de área, la probabilidad conjunta de que ambos eventos se produzcan juntos estaría representada por la intersección de las dos áreas de probabilidades, según lo ilustrado conceptualmente abajo.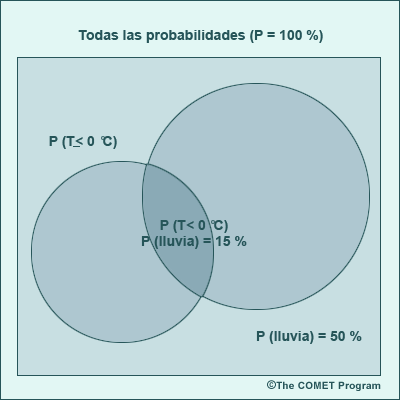
La intersección de esas áreas de probabilidad es equivalente a contar el porcentaje de veces que ambos eventos ocurren al mismo tiempo. Observe que el concepto de probabilidad conjunta se puede ampliar para que abarque tres o más eventos.
En la predicción por conjuntos, se cuentan los miembros del conjunto que muestran la ocurrencia de ambos eventos en una celda de la malla. Dividiendo el resultado entre el número total de miembros del SPC se obtiene la probabilidad conjunta de que ocurran ambos eventos.
Tabla de probabilidad conjunta
Supongamos que tenemos una predicción por conjuntos a corto plazo de 36 horas con 15 miembros. La tabla siguiente muestra los dos eventos de interés (temperatura ≤ 0 °C y lluvia) en filas separadas. Un valor de 1 indica un miembro del conjunto en el cual se produce el evento y 0 lo contrario. La tercera fila indica los miembros en los cuales se producen lluvia y temperaturas bajo cero
|
Evento\Miembro del conjunto
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15 |
Total
|
|
Lluvia
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
9
|
|
Temperatura |
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
7
|
|
Lluvia y temperatura
≤ 0 °C |
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
4
|
En 9 de los 15 miembros hay lluvia (frecuencia de 0,6) y siete de los 15 miembros tienen temperaturas por debajo de cero grados (frecuencia de 0,467). De los 15 miembros, solo en 4 se producen ambos eventos al mismo tiempo, con una frecuencia de 0,267. Tres de los miembros no pronosticaron ni lluvia ni temperaturas por debajo de cero grados.
Observe que no podemos determinar la probabilidad conjunta de que dos eventos ocurran al mismo tiempo solo en base a la frecuencia de cada evento individual. Ilustramos esta limitación en la siguiente tabla de probabilidad conjunta. Los eventos están organizados en filas y columnas. Las celdas internas muestran la frecuencia de los acontecimientos que se producen simultáneamente, mientras que las celdas de los márgenes dan la probabilidad total de los eventos. La celda de la esquina inferior derecha debe tener un valor de 1,00, resultado de la suma de las frecuencias de los eventos de si y de no. De este modo, la probabilidad de eventos de lluvia (0,6) frente a los eventos sin lluvia (0,4) y de eventos con temperaturas bajo cero (0,467) frente a los eventos con temperaturas por encima de cero (0,533) se ponen en las filas y columnas correspondientes.
|
Eventos
|
Temperatura
> 0 °C |
Temperatura
≤ 0 °C |
Total marginal
|
|
Con lluvia
|
?
|
?
|
0,600
|
|
Sin lluvia
|
?
|
?
|
0,400
|
|
Total marginal
|
0,533
|
0,467
|
1,000
|
Las probabilidades marginales deben sumar 1,00 y la suma de las filas y columnas de las celdas internas debe ser igual a las frecuencias marginales. Observe que no es posible determinar ninguno de los valores internos sin disponer de una de las cuatro posibles probabilidades conjuntas. Si introducimos la probabilidad conjunta de lluvia y temperaturas ≤ 0 °C en la tercera columna de la segunda fila de la tabla, se pueden calcular el valor de las otras tres células.
|
Eventos
|
Temperatura
> 0 °C |
Temperatura
≤ 0 °C |
Total marginal
|
|
Con lluvia
|
0,600 – 0,267 = 0,333 |
0,267
|
0,600
|
|
Sin lluvia
|
0,533 – 0,333 = 0,200
|
0,467 – 0,267 = 0,200
|
0,400
|
|
Total marginal
|
0,533
|
0,467
|
1,000
|
Pregunta: distribuciones de probabilidad conjunta
Los mapas que generalmente obtenemos de los sistemas de predicción por conjuntos para los tipos y la cantidad de precipitación muestran, respectivamente, la probabilidad de ocurrencia o la probabilidad de superar un umbral determinado, según el número de miembros que satisfacen los criterios establecidos. Usted tiene la información siguiente acerca de una predicción por conjuntos:
- hay un 50 % de probabilidad de que se produzcan 15 mm o más de precipitación en las próximas 12 horas;
- la probabilidad de nieve es del 42 %;
- todos los miembros pronosticaron la precipitación como nieve o como lluvia.
Pregunta
¿Qué podemos decir acerca de la probabilidad de que nieve y se produzcan más de 15 mm de precipitación en las próximas 12 horas? Elija la mejor respuesta.
La respuesta correcta es d).
No se puede determinar la probabilidad conjunta de que nieve y se produzcan más de 15 mm de precipitación en las próximas 12 horas sobre la base de la probabilidad de cada evento individual. Si tuviéramos por lo menos uno de los valores de probabilidad conjunta, podríamos calcular el resto. Por ejemplo, si hay un 0,25 % de probabilidad de que en las próximas 12 horas caigan 15 mm de nieve o más, podemos insertar este valor en la tabla de abajo y calcular las otras probabilidades conjuntas:
|
Eventos
|
Precip.
< 15 mm |
Precip.
> 15 mm |
Probabilidad marginal
|
|
Nieve
|
0,17
|
0,25
|
0,42
|
|
Lluvia
|
0,33
|
0,25
|
0,58
|
|
Probabilidad marginal
|
0,50
|
0,50
|
1,00
|
Ahora que sabemos la probabilidad conjunta (0,25) para precipitación ≥ 15 mm y nieve y la probabilidad marginal de nieve (0,42), podemos calcular la probabilidad conjunta para precipitación < 15 mm y nieve (0,42 - 0,25=0,17). A continuación, podemos calcular la probabilidad de lluvia y precipitación ≥ 15 mm (0,50 - 0,25=0,25) y, finalmente, la probabilidad de lluvia y precipitación < 15 mm (0,58 - 0,25=0,33).
Cabe resaltar que aceptar estas probabilidades generadas por conjuntos tal cual requiere suponer que el modelo es perfecto y toda la incertidumbre está en las condiciones iniciales. Como bien sabemos que el modelo no es perfecto, habrá que ajustar las salidas del conjunto para tomar en cuenta los errores y sesgos del modelo. Aquí, por ejemplo, el modelo suaviza la topografía considerablemente con respecto a la topografía real y por tanto podría resultar apropiado ajustar la probabilidad de nieve según los niveles de congelamiento esperados para generar los pronósticos dependientes de la altura. Hablaremos de los ajustes que se pueden hacer a través del posprocesamiento de las predicciones por conjuntos en la sección «Verificación» de esta lección.
Centralidad
Se utilizan varias medidas estadísticas para describir la distribución de una distribución teórica de datos en términos de la posición de su «centro» o tendencia central, de su variabilidad o dispersión y de su forma general. En esta sección trataremos la estadística usada para la tendencia central; las próximas dos secciones presentan información sobre la estadística de la variabilidad y la forma de la distribución.
¿Dónde está el centro de los datos? Ciertas medidas estadísticas nos dan una noción de donde está el centro de una muestra de los datos, pero puesto que se utilizan diversos conceptos centralidad, pueden darse respuestas muy diversas cuando los datos no se ajustan a la forma de campana de una distribución normal. En las secciones siguientes se describen tres conceptos diferentes de centralidad.
Media aritmética o promedio
La media aritmética o promedio de una muestra de datos es simplemente la suma de los valores dividida por el número total de valores, es decir:
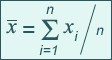
donde x es la variable de interés, la barra horizontal sobre la x indica una cantidad media y n es el número de valores.
Mediana
Si organizamos un conjunto de datos de menor a mayor, el valor central que deja a cada lado (por encima y por debajo) la mitad de los datos es la mediana de la muestra. Observe que al tomar la mediana se reduce la influencia de los valores extremamente altos y/o bajos (los valores atípicos) de la muestra de datos, que pueden hacer que la media sea menos representativa del verdadero centro. Si el número de datos organizados es par, la mediana se define como el promedio de los valores N/2 y (N/2 + 1).
Moda
La estadística de tendencia central dada por el valor o intervalo observado más con mayor frecuencia es la moda de la muestra de datos. Ninguno de los valores en la muestra, con excepción de los que están en la categoría de mayor frecuencia de observación, afecta al valor de la moda.
Para ilustrar cada una de estas medidas de tendencia central, puede ver un ejemplo que utiliza datos reales generados por el conjunto del modelo para el 16 de agosto de 2004. Este conjunto de datos se utilizará en las próximas páginas para continuar ilustrando el uso de las medidas estadísticas que estamos presentando.
Ventajas y desventajas de las medidas de tendencia central
La siguiente tabla muestra una lista de las ventajas y desventajas de las medidas de tendencia central que acabamos de presentar.
|
Estadística |
Ventajas |
Desventajas |
|
Media |
• Toma en cuenta todos los datos de la muestra. • Para las distribuciones normales, es la medida de tendencia central más estable cuando se utiliza una muestra de datos para deducir la tendencia central de una población mayor. |
• No es representativa de la tendencia central cuando la muestra de datos es asimétrica (vea la sección Forma). • Puede verse fuertemente afectada por los valores extremos, particularmente en el caso de muestras pequeñas. |
|
Mediana |
• No se ve afectada por los valores extremos. • Da buenos resultados para las distribuciones sesgadas (asimétricas). |
• Se deben clasificar los datos. • No utiliza todos los valores de datos. |
|
Moda |
• No se ve afectada por los valores extremos. • Se puede utilizar para datos no numéricos (por ejemplo, el tipo de precipitación). • Puede descubrir múltiples valores máximos (si tienen la misma frecuencia). |
• No utiliza todos los datos. • Es sensible a la forma en que se determinan los intervalos de datos. |
Pregunta: ceentralidad
Pregunta
Si usted desea considerar todos los datos de un conjunto de datos para describir el valor medio de los datos, ¿qué estadística de valor central utilizaría? Elija la mejor respuesta.
La respuesta correcta es b), la media, porque se calcula utilizando todos los datos.
La mediana es el valor que se encuentra en el medio una vez que se ordenen los datos desde el valor más bajo al más alto y la moda es el valor que se produce con mayor frecuencia, de modo que ambas estadísticas ignoran algunos valores. Por lo tanto, las respuestas a), c) y d) son incorrectas.
Variabilidad
Medidas de variabilidad
Ahora que hemos considerado las estimaciones de tendencia central o centralidad de los datos del conjunto, veamos las medidas de variabilidad que nos permiten tener una mejor noción de la dispersión de los datos. Una buena medida de la variabilidad utiliza todos los datos y aumenta a medida que aumenta la dispersión de la población o de la muestra de datos.
Desviación típica (S)
La primera de estas medidas, la desviación típica (que se suele representar por una S), supone que los datos tienen una distribución normal. La desviación típica es la raíz cuadrada de la varianza, que es el promedio del cuadrado de las diferencias entre cada dato y la media de la muestra de datos. La fórmula para calcular la desviación típica es:
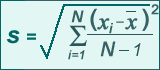
donde N es el tamaño de la muestra de datos, x es la variable de interés y S es la desviación típica de la muestra. En la fórmula, N se reduce a N-1, porque se puede mostrar que cuando se usa N en el denominador se subestima la verdadera varianza (de la población).
El valor de S se utiliza para medir la distancia con respecto al promedio. Como podemos ver en el gráfico siguiente, en una distribución normal aproximadamente el 68 % de los datos está entre ±1 S, cerca del 95 % de los datos está entre ±2 S y cerca del 99,8 % de los datos está dentro de ±3 S del promedio.
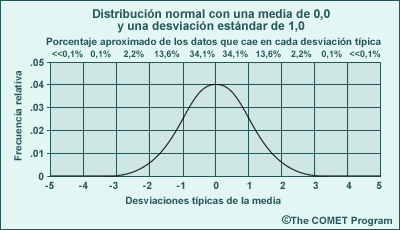
Puede ver un ejemplo de cómo calculamos la desviación típica en nuestra muestra de datos de conjuntos de las temperaturas a nivel de 2 m en el ciclo de ejecución del conjunto del 16 de agosto de 2004.
Ordenamiento de los datos en percentiles
Otra manera de describir los datos del conjunto consiste en organizarlos de modo que se pueda describir la posición relativa de un miembro particular dentro del conjunto completo. Una medida denominada percentil expresa esta posición en términos de porcentajes. El percentil de un valor da el porcentaje del conjunto de datos total que cae por debajo de ese valor. La mediana, por definición, es el percentil 50.
Rangos de percentil de uso común
Los cuartiles se utilizan para describir los datos separados en 4 partes iguales y corresponden al percentil 25, la mediana y el percentil 75. Por lo tanto, el percentil 25, la mediana y el percentil 75 son, respectivamente, los puntos de separación entre el primero y el segundo cuartil, el segundo y el tercer cuartil, y el tercer y el cuarto cuartil de un grupo de datos.
Los deciles separan los datos en 10 partes iguales correspondientes al 10 % cada una y separan los datos en los percentiles 10, 20, 30 y así sucesivamente hasta el percentil 90.Si un percentil cae entre dos valores ordenados, el punto de separación del percentil está determinado por la interpolación entre los valores del rango. Por ejemplo, la tabla siguiente contiene 13 datos ordenados y separados por cuartiles. La primera fila numera los datos del valor más bajo al más alto y muestra el punto de separación de los cuartiles; la segunda fila contiene los datos; la tercera fila muestra los cuartiles y los valores interpolados del punto de separación.
|
Número de datos |
1 |
2 |
3 |
3,25 |
4 |
5 |
6 |
6,5 |
7 |
8 |
9 |
9,75 |
10 |
11 |
12 |
13 |
|
Datos |
14 |
18 |
22 |
|
25 |
30 |
36 |
|
39 |
42 |
47 |
|
48 |
55 |
58 |
60 |
|
Separación en cuartiles |
1er cuartil |
22,75 |
2o cuartil |
37,5 |
3er cuartil |
47,75 |
4o cuartil |
|||||||||
Cada cuartil debe contiene 3,25 valores ordenados, así que los puntos de separación de los cuartiles son 3,25, 6,5 y 9,75. Observe que los valores de la tercera fila se obtuvieron interpolando entre los valores superior e inferior de los datos organizados.
Datos del conjunto del 16 de agosto de 2004: variabilidad
Clasificación de los datos en cuartiles
La tabla siguiente muestra los datos ordenados de las temperaturas a 2 m que ya usamos antes, pero separados en cuartiles. Como la muestra de datos no se puede dividir entre cuatro, los límites entre los intervalos caerán entre dos puntos ordenados consecutivos. Aquí cada cuartil contiene 41/4 ó 10,25 elementos ordenados, de modo que los límites entre los cuartiles se dan en 10,25, 20,5 y 30,75.
| Secuencia |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
10,25 |
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
20,50
|
|
| Cuartil |
1er cuartil
|
2o cuartil | |||||||||||||||||||||
| Temperatura a 2 m | 73 | 74 | 75 | 75 | 75 | 77 | 77 | 79 | 79 | 80 |
80
|
80 | 81 | 81 | 82 | 82 | 82 | 82 | 82 | 82 | 83 |
83
|
|
| Secuencia | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 30,75 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
41
|
|
| Cuartil |
3er cuartil
|
4o cuartil
|
|||||||||||||||||||||
| Temperatura a 2 m | 83 | 83 | 84 | 84 | 84 | 84 | 84 | 84 | 84 | 85 |
85
|
85 | 85 | 85 | 85 | 86 | 86 | 86 | 87 | 87 | 87 |
87
|
|
Los valores de los elementos ordenados inmediatamente antes y después de los límites de los intervalos son iguales, de modo que no hace falta interpolar. Sin embargo, si los valores fuesen diferentes, sería necesario interpolar entre los datos ordenados antes y después. Por ejemplo, si el valor del elemento número 10 de la tabla fuera 80 °F y el del elemento 11 fuera 82 °F, el valor del cuartil sería 0,25*(82-80)+80 = 80,5 °F.
Pregunta: variabilidad
Pregunta
¿Cuál de las siguientes estadísticas de variabilidad requiere que los datos estén distribuidos normalmente para ser estrictamente válido? Elija la mejor respuesta.
La respuesta correcta es c)
La desviación típica se deriva directamente de la distribución normal. Los deciles y los cuartiles son ejemplos de la organización en percentiles y no requieren ningunas suposición particular sobre la distribución de los datos. Por lo tanto, las respuestas a), b) y d) son incorrectas.
Forma
Los pronosticadores experimentados comprenden claramente que muchos procesos atmosféricos no son normales y que tampoco presentan distribuciones normales. Por el contrario, con frecuencia el comportamiento caótico de la atmósfera y los límites físicos impuestos sobre los valores numéricos producen funciones de densidad de probabilidad (FDP) asimétricas. Entre los procesos y las cantidades que presentan distribuciones asimétricas podemos mencionar los eventos individuales de precipitación, la nubosidad y la humedad relativa. ¿Cómo podemos medir esta asimetría?
Asimetría
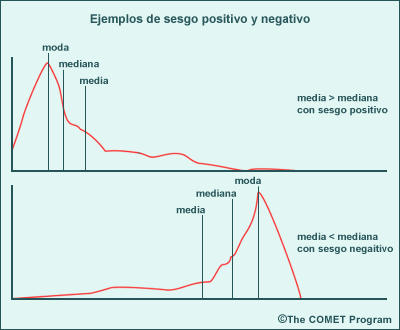
La asimetría, o sesgo, mide la posición de la media con respecto a la distribución total. Una distribución normal tiene asimetría 0,0, igual que cualquier otra FDP perfectamente simétrica. Una FDP con asimetría positiva, es decir, «con asimetría a la derecha» tendrá su frecuencia máxima (su moda) a la izquierda de la mediana y la media aritmética a la derecha, hacia una cola larga. Una FDP con asimetría negativa, o «a la izquierda», tendrá su frecuencia máxima a la derecha de la mediana y de la media aritmética, y una cola larga a la izquierda. El gráfico siguiente muestra unos ejemplos hipotéticos de los dos casos.
Funciones de densidad de probabilidad multimodales
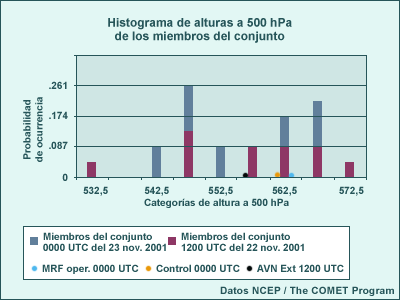
Las distribuciones de probabilidad de pronósticos del sistema de predicción por conjuntos (SPC) no se ajustan a las distribuciones teóricas que hemos contemplado hasta ahora. Es común observar distribuciones que presentan más de un pico. Estas distribuciones se conocen como distribuciones multimodales. Un ejemplo de una FDP bimodal (con dos picos) puede verse en el diagrama que sigue, el cual muestra las probabilidades para los valores de alturas a 500 hPa de dos ciclos de ejecución del conjunto (separados en clases de 5 dm, de un total de 21 miembros del conjunto) para el 23 de noviembre de 2001. Se observa un máximo de probabilidad en 547,4 dm y otro en 567,5 dm. Aunque hay solamente una moda verdadera para la distribución, la presencia de valores pico similares, pero separados, hace que esta y otras estadísticas de «valor central» resulte de escasa utilidad. Por ejemplo, ¿cuán representativas del centro son la media y la mediana de la distribución de abajo, especialmente si consideramos que sus valores caen entre dos clases con solamente 2 miembros del conjunto, rodeadas por clases con probabilidades mucho más altas?
Una FDP con múltiples máximos de probabilidad puede indicar que
- la predicción por conjuntos no cuenta con suficientes miembros para dar una lectura exacta
de las probabilidades de salidas de los pronósticos resultante
o, con más frecuencia, que
- existen múltiples regímenes de flujo que tienen probabilidades considerables de poderse verificar.
Volveremos a tocar el tema de las distribuciones multimodales en la sección Resumen de los datos, al hablar de las limitaciones del uso de los productos Media y dispersión del conjunto.
A fondo: Asimetría y curtosis
Asimetría
A veces es conveniente saber en qué medida están sesgados los datos con respecto a una distribución normal simétrica. Las distribuciones asimétricas se producen cuando las cantidades de interés tienen características físicas que limitan sus valores, como la cantidad de precipitación diaria (con un límite inferior en cero y limitaciones físicas en la precipitación máxima posible) y la velocidad del viento (límite inferior en cero y limitaciones físicas de los valores máximos basadas en el gradiente de presión, la viscosidad y la fricción).
La fórmula para el parámetro de asimetría o sesgo es:
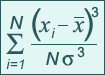
Curtosis
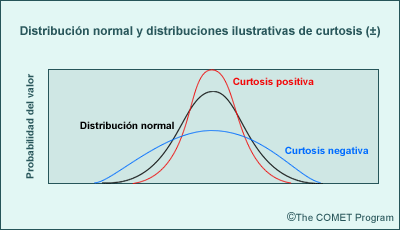
La curtosis mide el tamaño de la cola en la FDP de una muestra comparada con una distribución normal teórica. Una curtosis positiva indica una distribución con un pico más pronunciado y una curtosis negativa indica una distribución «achatada» (es decir, colas más cortas y más largas, respectivamente, que en una distribución normal).
Como la curtosis de una distribución normal es de 3,0, en la fórmula de exceso de curtosis se resta 3 del parámetro de curtosis:
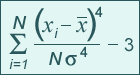
Pregunta: forma
Pregunta
Usted calcula la asimetría de un conjunto de datos de precipitación y encuentra que el valor resultante es mayor que cero. ¿Cuáles de las afirmaciones siguientes son verdaderas? Elija todas las que correspondan.
Las respuestas correctas son a) y d).
Cuando los valores de asimetría son mayores que cero, se dice que los datos tienen asimetría positiva. En tal conjunto de datos, la mayoría de los valores están agrupados hacia los valores más pequeños y su distribución tiene una larga cola hacia los valores altos. Con una distribución de datos como esta, la media será mayor que la mediana debido a la influencia de los valores altos en la cola de la distribución. Esto significa que las respuestas a) y d) son correctas, mientras que b) y c) son incorrectas.
Uso de las funciones de densidad de probabilidad (FDP)
Uso de la FDP en el proceso de pronóstico: cálculo de la probabilidad de un evento
Las distribuciones de probabilidad, o FDP, se utilizan al menos de forma implícita en la mayoría —por no decir en todos—los aspectos del proceso de pronóstico. Esta sección presenta los métodos que usamos con frecuencia para determinar la probabilidad de un evento meteorológico específico.
Métodos no basados en los modelos de PNT
Mucho antes de que existieran los modelos de PNT, se hacía uso de las distribuciones de probabilidad obtenidas de las observaciones para pronosticar el tiempo. Para utilizar estos métodos es necesario considerar:
- la climatología local, para evaluar el probable valor futuro de las variables a pronosticar;
- los valores actuales de las variables meteorológicas usadas en la elaboración del pronóstico (persistencia); y
- la evolución de la atmósfera en situaciones similares en el pasado (pronósticos análogos).
El uso de algunos de estos métodos sigue siendo apropiado en el proceso de pronóstico actual, al menos como forma de «comprobar» lo que sugiere el modelo de PNT.
A modo de ejemplo, en esta gráfica la distribución de probabilidad de la media diaria observada de las alturas a 500 hPa para una celda de malla de 2,5 x 2,5 grados en 42.5°N, 125°O (basada en los reanálisis de NCAR/NCEP de enero de 1979 a diciembre de 1995 interpolados para el 28 de noviembre) se muestra en azul. Las columnas violetas representan una muestra de datos de distribución normal con la misma media y desviación típica. En este caso, la distribución climatológica se ajusta bien a una distribución gaussiana.

(Nota acerca de la gráfica: debido a que los datos teóricos se agruparon en clases de 50 metros no centradas en la media, la distribución gaussiana tiene un aspecto levemente asimétrico.)
Dado el conjunto de datos climatológicos anterior, si un modelo de PNT estuviese pronosticando un valor promedio de 520 dm para la altura de 500 hPa en la celda de interés para el 28 de noviembre, sería buena idea revisar ese pronóstico e incluso considerar la posibilidad de rechazarlo. Volveremos a ver esta climatología cuando examinemos los datos del conjunto válidos para el 22 de noviembre de 2001, en la próxima sección.
Métodos que utilizan un único pronóstico de PNT
De acuerdo con nuestra experiencia en situaciones de pronóstico semejantes, utilizamos las distribuciones de probabilidad de manera informal en el proceso de pronóstico todos los días. Por ejemplo, podríamos advertir la probabilidad de que se alcancen niveles críticos de índice de calor basándonos en parte en los pronósticos de PNT para la temperaturas en el nivel de 850 hPa y la humedad relativa en la capa límite planetaria. Al hacerlo, estamos esencialmente colocando estas variables del modelo en una distribución de probabilidad subjetiva de los niveles críticos de índice de calor.
También se pueden emplear métodos objetivos cuando se utiliza un único pronóstico de PNT. Por ejemplo, la página del Centro de Predicción Hidrometeorológica (Hydrometeorological Prediction Center, o WPC) proporciona estadísticas sobre las asimetría de los modelos de PNT operativos para los cinco o diez días anteriores. Es posible encontrar información similar en algunas de las páginas de diagnóstico de los modelos del Centro de Modelado Ambiental (Environmental Modeling Center, o EMC).
¿Cómo podríamos utilizar el error estadístico del modelo en la práctica? Supongamos que para un determinado lugar X tenemos una muestra de 1000 pronósticos (en violeta) y los análisis de verificación (en azul) del modelo Eta para las temperaturas a 850 hPa del mes de julio, la cual tiene una distribución como la siguiente:
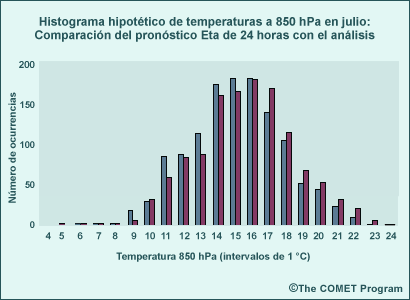
Resulta que la media de la muestra del análisis es 14,6 °C, con una desviación típica de 2,9 °C. Los pronósticos de 24 horas, sin embargo, tienen una media de 15,1 °C y (para simplificar) la misma desviación típica. La gráfica siguiente muestra la distribución de los errores para el mismo pronóstico de 24 horas.
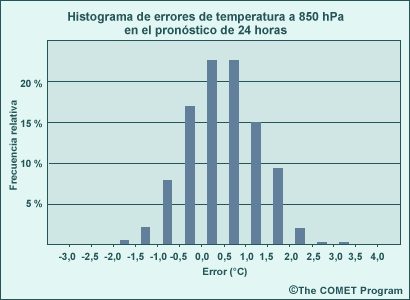
Como se esperaba, el error medio (0,5 °C) es igual a la diferencia entre las medias de los pronósticos y de las verificaciones; el error también tiene una distribución normal. Esto representa la asimetría del pronóstico de 24 horas para esta muestra. La desviación típica del error es 0,8 °C. Para cualquier pronóstico de 24 horas de la temperatura a 850 hPa, podemos utilizar la asimetría de la muestra junto con el pronóstico de 24 horas para estimar el valor más probable de la temperatura en 850 hPa. La dispersión del error nos da una medida de la incertidumbre del pronóstico de temperaturas en el nivel de 850 hPa.
Por lo tanto, si el modelo Eta pronostica una temperatura de 15,5 °C en el nivel de 850 hPa para dentro de 24 horas, podemos utilizar este método para calcular que el valor de esa temperatura será de 15 °C, con una probabilidad del 67 % (±1 desviación típica) de que la temperatura estará entre 14,2 y 15,8 °C.
Sin embargo, los datos a partir de los cuales se derivaron las estadísticas incluyen varios pronósticos diferentes generados bajo varios regímenes distintos. Es posible que el error de la temperatura en 850 hPa dependa del régimen. Por ejemplo, bajo condiciones húmedas el pronóstico de temperatura tiende a ser muy alto debido al exceso del flujo de calor sensible de la superficie del modelo, mientras que en condiciones secas el pronóstico de temperatura es demasiado bajo, por razones análogas. Este tipo de información no está disponible en la muestra.
Además, necesitamos la información de un modelo «congelado», para saber que el error estadístico del modelo es estable (los cambios en un modelo pueden cambiar los errores característicos de ese modelo, algo que ocurre con frecuencia). Si debido a cambios realizados en el modelo la asimetría hacia el calor antes señalado se elimina, se reduce o se sustituye por una asimetría hacia el frío, el rango de valores de temperatura esperados para el nivel de 850 hPa se basará en datos incorrectos.
Métodos que utilizan pronósticos por conjuntos
El uso de funciones de densidad de probabilidad elaboradas a partir de las relaciones entre las observaciones y las variables del modelo, como se mostró en los ejemplos anteriores, puede ser útil en el proceso del pronóstico. Sin embargo, existen ciertas desventajas. Por ejemplo, a menudo las relaciones entre los pronósticos del modelo y la verificación subsiguiente dependen del régimen del flujo, lo que significa que la aplicación de estas relaciones no será válida en algunos casos. Tampoco proporciona una medida cuantitativa de la predictibilidad del régimen del flujo.
Un método lógico para evitar estos problemas consiste en utilizar pronósticos por conjuntos para obtener una FDP de los posibles resultados del pronóstico. Los pronósticos por conjuntos tienen claras ventajas sobre los pronósticos deterministas simples, porque toman en cuenta los siguientes aspectos:
- la incertidumbre de la condición inicial actual y la predictibilidad atmosférica;
- el efecto del régimen del flujo actual sobre la predictibilidad y los sesgos del modelo de PNT;
- la configuración actual del modelo (las versiones anteriores del modelo de PNT pueden tener diferentes errores y sesgos característicos).
Además, cuando están calibrados apropiadamente los conjuntos se pueden ajustar para tomar en cuenta las imperfecciones de los modelos de PNT y el desempeño reciente de los modelos de manera sistemática y objetiva. Esto se considerará más adelante, en las secciones Productos y Verificación.
Obviamente, el número de pronósticos que podemos incluir en una ejecución del conjunto estará limitado por la capacidad computacional disponible para crear los diferentes miembros del conjunto y esta limitación es importante porque significa que debemos construir con cuidado nuestro sistema de predicción por conjuntos (SPC). En la próxima sección, Aplicación de los datos, examinaremos una distribución de la probabilidad de un par de ciclos de ejecución consecutivos del conjunto del NCEP.
Pregunta: métodos que utilizan pronósticos por conjuntos
Pregunta
¿Cuáles son las ventajas de utilizar pronósticos por conjuntos sobre otros métodos, como la climatología, para determinar la probabilidad de un evento? Elija todas las opciones pertinentes.
Las respuestas correctas son a), b) y d).
En virtud de cómo se crean las perturbaciones de la condición inicial en los sistemas de predicción por conjuntos, los aspectos de predictibilidad e incertidumbre actual de las condiciones iniciales se consideran automáticamente en las predicciones por conjuntos. Estas perturbaciones se crean en tiempo real en base a la incertidumbre de las condiciones iniciales a la cual el régimen del flujo actual es más sensible. Esto significa que las respuestas a) y b) son correctas. Sin embargo, las asimetrías y los errores sistemáticos del modelo no se toman en cuenta al perturbar las condiciones iniciales. No obstante, la calibración basada en el desempeño en el pasado puede mejorar las predicciones por conjuntos. Por consiguiente, la respuesta c) es incorrecta y la respuesta d) es correcta.
Aplicación de los datos
Aplicación de la estadística a una muestra de datos de conjuntos
Para ayudar a entender mejor la salida de un SPC, ilustraremos cómo se aplican los conceptos estadísticos a un caso real de verificación para el 28 de noviembre 2001. Examinaremos los ciclos del 22-23 de noviembre de 2001 del SPC del Sistema de Pronóstico Global (Global Forecast System, o GFS) del NCEP, que también se conoce como AVN/MRF. En aquel entonces, este sistema utilizaba perturbaciones de las condiciones iniciales para crear 23 ciclos de ejecución o «miembros» del conjunto diferentes por día. Los miembros del conjunto se ejecutaron en T62 con 28 niveles, mientras que en T170 se ejecutó un control de alta resolución con 42 niveles. Hay 12 miembros a partir de las 0000 UTC, lo cual incluye el ciclo operacional de las 0000 UTC y un ciclo de ejecución de control de baja resolución del conjunto a las 0000 UTC y 11 ciclos a partir de las 1200 UTC, incluyendo la extensión del AVN en uso en ese entonces, a las 1200 UTC.
El mapa que aparece a continuación muestra un «diagrama espagueti» (encontrará más información sobre los diagramas espagueti en la sección Resumen de los datos) del trazado de la isohipsa de 5520 m a 500 hPa de cada miembro del conjunto para los pronósticos válidos a las 1200 UTC del 28 de noviembre de 2001 (día 6). Debajo del mapa aparece la leyenda que permite interpretar los colores de las isohipsas: amarillo y verde corresponden a los resultados de los miembros del conjunto a partir de las perturbaciones; negro y azul a los resultados de los modelos operacionales; naranja a la pasada de control del conjunto. Observe que el SPC presenta un grado de incertidumbre considerable en el pronóstico de la isohipsa de 5520 m sobre el Pacífico Este y la zona oeste adyacente de Norteamérica, mientras que las pasadas operacionales son más coherentes entre sí. La «X» roja en el gráfico (en 125°O, 42.5°N, cerca de la costa central del estado de Oregón) representa la posición aproximada del lugar donde obtendremos los datos de 500 hPa para el análisis estadístico de la salida del conjunto.
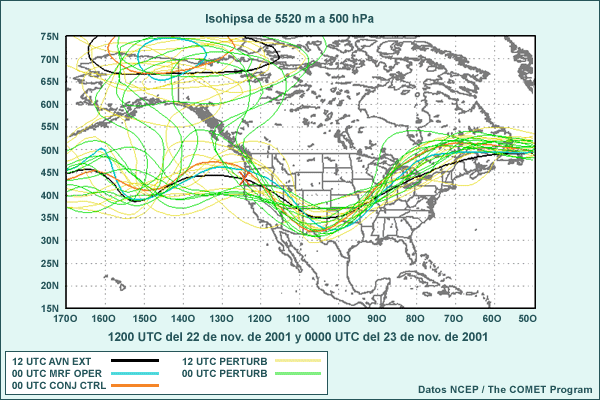
Distribución de los datos del conjunto
Primero, examinemos la distribución de los datos brutos de alturas a 500
hPa en 125°O, 42.5°N de los ciclos de ejecución del conjunto de las 1200 UTC del 22
de noviembre y de las el 0000 UTC del 23 de noviembre de 2001. Los datos aparecen en las
tablas siguientes.
|
1200 UTC 22 de noviembre de 01
|
||||||
| Miembro del conjunto | AVN EXT | p1 | p2 | p3 | p4 | p5 |
| Altura a 500 hPa | 5553,5 | 5452,4 | 5646,7 | 5320,9 | 5709,4 | 5483,1 |
| n1 | n2 | n3 | n4 | n5 | ||
| 5652,6 | 5555,1 | 5696,5 | 5452,6 | 5620,5 | ||
|
0000 UTC 23 de noviembre de 01
|
|||||||
| Miembro | MRF OPER | CONJ CTRL | p1 | p2 | p3 | p4 | p5 |
| Altura a 500 hPa | 5620,6 | 5602,5 | 5474,7 | 5505,7 | 5435,6 | 5409,9 | 5659,6 |
| n1 | n2 | n3 | n4 | n5 | |||
| 5549,9 | 5499,0 | 5654,6 | 5670,6 | 5452,4 | |||
Para trazar los datos gráficamente, primero establecemos los intervalos o «clases» de alturas y luego determinamos qué porcentaje del total de los miembros del conjunto cae en cada uno de dichos intervalos o clases. A continuación creamos un gráfico de columnas o histograma de esos porcentajes de las alturas pronosticadas de 500 hPa en el punto de interés. Las columnas se codifican con colores, tal como lo indica la leyenda. Los valores han sido clasificados en intervalos de 5 decámetros (dm) entre 530 y 575 dm. También hemos indicado en el histograma los valores específicos de los pronósticos de la extensión AVN de las 1200 UTC del 22 de noviembre y de los pronósticos de control del conjunto y del modelo MRF operacional de las 0000 UTC del 23 de noviembre de 2001, cada uno mediante punto de color. Observe que los valores de altura de estos pronósticos están incluidos en los conteos del histograma.

Podemos ver que hay una distribución más amplia de los miembros del conjunto de las 1200 UTC del 22 de noviembre de 2001 que para el ciclo de ejecución siguiente del conjunto, a las 0000 UTC del 23 de noviembre.
Estadísticas de tendencia central
El gráfico siguiente muestra el mismo histograma que antes, pero ahora incluye las tres estadísticas de tendencia central calculadas para la muestra de datos con la que hemos estado trabajando.
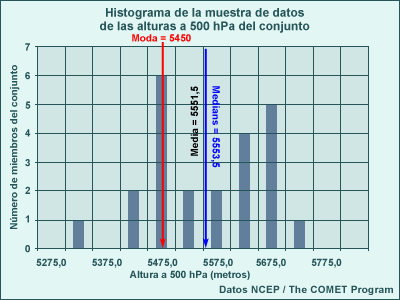
El gráfico nos permite observar que el valor medio, que se halla aproximadamente en el centro de la distribución, es de 5551,5 m. Como la media está casi exactamente en el centro de los datos, la mediana y la media están bastante próximas. Sin embargo, la moda se encuentra en el intervalo de 50 metros entre 5450 y 5500 m. Observe que este valor se diferencia significativamente de las otras medidas de tendencia central; también note que hay un segundo máximo en el intervalo de 5650 a 5700 m, no contemplado por la moda.
En situaciones donde hay más de un agrupamiento o aglomeración de datos, la estadística de centralidad, que por definición puede producir un solo valor, no representará la solución más probable. Esto es lo contrario de la interpretación usual, por ejemplo, que la media del conjunto representa el valor más probable.
Ejercicios
Tendencia central (centralidad)
Pregunta

Después de un análisis visual de la FDP de la muestra de datos del conjunto para la altura a 500 hPa en 42,5°N, 125°O, ¿qué estadística de tendencia central sería más útil en el proceso de pronóstico?
Elija todas las opciones pertinentes.
La respuesta correcta es d).
Para que la media y la mediana sean representativas del «valor más probable de pronóstico», los datos deben mostrar la tendencia a caer cerca de un valor central. Aquí, por lo contrario, los datos caen en un área de valores altos y otra de valores bajos. La moda no es confiable, porque considera solamente una de estas áreas.
Para entender mejor la distribución de los datos en comparación con la tradicional distribución gaussiana a partir de la cual se suelen interpretar las estadísticas de media y desviación típica, construimos un histograma de Gauss teórico para el conjunto de datos de 23 miembros que compara la media y la desviación típica climatológica presentadas previamente para el 28 de noviembre con los datos reales de la muestra de los miembros del conjunto de las 1200 UTC del 22 de noviembre y de las 0000 UTC del 23 de noviembre de 2001. El resultado se muestra en este gráfico.
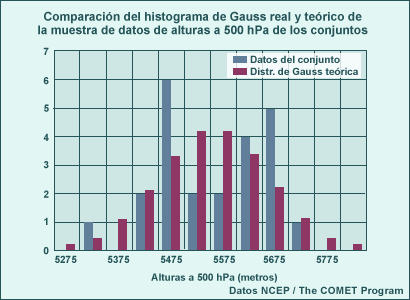
La distribución normal teórica está en color violeta y la distribución de la muestra de datos (para ambas pasadas del conjunto) en azul. Se aprecia en seguida que sería muy difícil ajustar los datos a una tradicional «curva en forma de campana» o distribución gaussiana. De hecho, los datos tienden a agruparse en dos intervalos distintos. Es común que se produzcan dos o más aglomeraciones como estas.
Dada una distribución como la anterior, ni la medida gaussiana de tendencia central (la media aritmética) ni la medida gaussiana de dispersión (la desviación típica de la muestra) serán muy significativas para describir los datos de la muestra. Si el estado de la atmósfera es tal que una distribución normal de posibles resultados de pronóstico ni siquiera es válida, como ocurre con el modelo de Lorenz simple de dos soluciones, ¡la estadística gaussiana puede incluso engañar! En tales situaciones, la función de distribución de probabilidad (FDP) del pronóstico brinda información más útil que los parámetros tradicionales de media, mediana, moda y desviación típica.
Es posible comprobar la «bondad de ajuste» de la distribución de una muestra de datos para una distribución teórica en particular. En la mayoría de las aplicaciones de pronóstico es suficiente una simple inspección visual de la función de distribución de probabilidad.
Estadísticas de variabilidad y forma
Para asegurar la completitud calculamos las estadísticas de variabilidad y forma para la muestra de datos de altura geopotencial al nivel de 500 hPa. El resultado es una desviación típica de 105,62 m, un sesgo de -0,25433 y una curtosis de -0,98297. Esto indica que si la muestra es representativa de la población de todos los pronósticos posibles, luego:
- existe un 66 % de probabilidad de que la verificación del pronóstico esté entre 545 y 566 dm (de acuerdo con la desviación típica), si la distribución de los datos es normal;
- los datos del pronóstico del conjunto presentan solo una leve desviación hacia la izquierda (el valor máximo más bajo es un poco mayor que el valor máximo más alto);
- la probabilidad de valores extremos es levemente mayor (es decir, es más probable que un valor caiga en las colas de la distribución de lo que sería el caso dada una distribución normal con las mismas estadísticas). Sin embargo, es probable que el pequeño valor de curtosis negativa refleje los valores máximos más altos en +1 y -1 desviaciones estándar respecto de la media y no un incremento en la probabilidad de valores positivos o negativos extremos.
Probabilidad conjunta
Los mapas que normalmente obtenemos del sistema de predicción por conjuntos para la cantidad y tipo de precipitación muestran, respectivamente, la probabilidad de ocurrencia o la probabilidad de superar un umbral. Los tres mapas que aparecen a continuación ilustran probabilidades a partir de la predicción por conjuntos a mediano plazo (Medium-Range Ensemble Forecast, o MREF) de las 0000 UTC del 20 de noviembre de 2001 válido para las 1200 UTC del 21 de noviembre 2001. Los tres mapas muestran los contornos de las probabilidades porcentuales de ocurrencia o superación en intervalos del 10 %. Nos concentraremos en la celda de 1 grado cuadrado ubicada en la cordillera de la Cascadas de Oregón, centrada en 44°N, 122°W (el cuadro rojo en cada mapa). También se muestra en rojo el porcentaje de probabilidad para el área seleccionada.
Probabilidad de > 13 mm de precipitación en 12 h
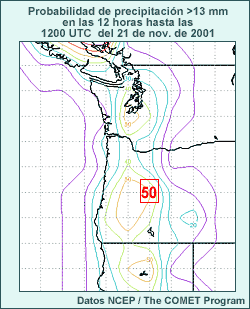
Probabilidad de lluvia mensurable como tipo de precipitación
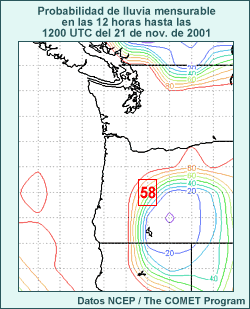
Probabilidad de nieve mensurable como tipo de precipitación
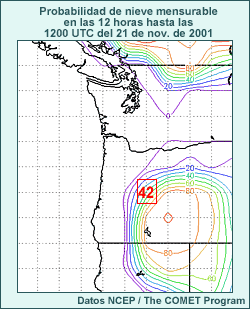
Considere ahora la información que tenemos. Ciertamente sería muy útil contar con algo más que las probabilidades indicadas en estos mapas. Para la probabilidad de una tormenta de invierno sería preciso contar con probabilidades conjuntas que combinen la probabilidad de tipo de precipitación y la probabilidad de cantidad. (Aunque no se muestra, observe que todos los miembros del conjunto presentan por lo menos 0,25 mm de precipitación en el área de interés).
| Evento | Precipitación mensurable < 13 mm | Precip. ≥ 13 mm | Total |
| Lluvia |
¿?
|
¿?
|
0,58
|
| Nieve |
¿?
|
¿?
|
0,42
|
| Total |
0,50
|
0,50
|
1,00
|
No podemos completar todas las celdas de la tabla de contingencia porque desconocemos las probabilidad conjunta de la ocurrencia del tipo de precipitación (lluvia o nieve) y la ocurrencia de la cantidad de precipitación en 12 horas que exceda 13 mm. Sin embargo, si tenemos los datos del tipo y la cantidad de precipitación de cada miembro del conjunto, podemos calcular la probabilidad conjunta contando los miembros en los que ocurre el tipo de precipitación de interés Y se excede el umbral de precipitación, y después dividir por el número total de miembros del conjunto. Por ejemplo, el mapa siguiente muestra la probabilidad de precipitación en 12 horas igual o mayor que 13 mm, en forma de nieve. La probabilidad porcentual para el área de la rejilla de interés se muestra otra vez en rojo.

Pregunta
¿Contamos con suficiente información en la tabla de contingencia siguiente para calcular otras probabilidades? Escoja las mejores opciones para completar la tabla. Cuando termine, haga clic en «Ver respuesta».
Las respuestas correctas son a) 0,33, b) 0,25 y c) 0,17
La clave para contestar esta pregunta está en recordar que las probabilidades marginales equivalen a la suma de todas las probabilidades de las respectivas filas o columnas.
Como tenemos la probabilidad conjunta de precipitación ≥ 13 mm y nieve (0,25) y la probabilidad marginal de nieve (0,42), podemos calcular la probabilidad conjunta de precipitación < 13 mm y nieve (0,42 - 0,25=0,17). A continuación podemos obtener la probabilidad de lluvia y precipitación ≥ 13 mm (0,50 - 0,25=0,25) y, finalmente, la probabilidad de lluvia y precipitación < 13 mm (0,58 - 0,25=0,33). En teoría, si el umbral para emitir un aviso en invierno fuera 12,5 cm de nieve en un período de 12 horas y suponemos una razón de 10:1 entre nieve y agua líquida equivalente, habría una probabilidad del 25 % que se produzca una nevada dentro del umbral de aviso durante el período entre las 0000 UTC y las 1200 UTC del 21 de noviembre de 2001.
Aceptar estas probabilidades generadas por conjuntos tal cual requiere suponer que el modelo es perfecto y toda la incertidumbre está en las condiciones iniciales. Como bien sabemos que el modelo no es perfecto, habrá que ajustar las salidas del conjunto para tomar en cuenta los errores y asimetrías del modelo. Aquí, por ejemplo, el modelo suaviza la topografía considerablemente con respecto a la topografía real y por tanto podría resultar apropiado ajustar la probabilidad de nieve según los niveles de congelamiento esperados para generar los pronósticos dependientes de la altura. Hablaremos de los ajustes que se pueden hacer a través del posprocesamiento de las predicciones por conjuntos en la sección «Verificación» de esta lección.
Resumen de los datos
Introducción
Nadie que participe en la generación de pronósticos operativos, especialmente en situaciones climáticas extremas, tendría tiempo para examinar los detalles de los diez o más miembros del conjunto de mediano plazo que se generan al ejecutar la predicción por conjuntos a mediano plazo (Medium-Range Ensemble Forecast, o MREF) del NCEP o los detalles de 15 o más miembros de la predicción por conjuntos a corto plazo (Short-Range Ensemble Forecast, o SREF) del NCEP. Uno de los problemas más comunes al utilizar los datos del SPC es el enorme volumen de datos. No sería la primera vez que alguien se diera por vencido ante la idea de tener que asimilar y tratar la gran cantidad de datos sin procesar. Por ejemplo, considere el mapa siguiente, que muestra las alturas a 500 hPa (en intervalos de 100 m) para los 11 miembros de la predicción por conjuntos de 84 horas a partir de las 0000 UTC del 19 de noviembre de 2001, válido para las 12 UTC del 22 de noviembre de 2001:
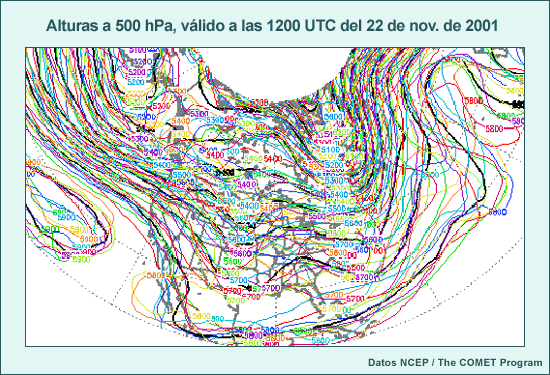
A pesar de que cada uno de los 11 miembros del conjunto tiene un color que lo distingue y que se identifican los valores de las isohipsas, ¡este mapa es de escasa utilidad!
Por lo tanto, para facilitar la interpretación de las previsiones de un SPC, las enormes cantidades de información contenidas en el pronóstico se agrupan en un número mucho más pequeño de productos estadísticos y gráficos. Este aspecto de la predicción por conjuntos —la generación de conjuntos de productos—aún está evolucionando, a medida que se descubren nuevas aplicaciones de la predicción por conjuntos para la meteorología operativa, por ejemplo para los pronósticos de tiempo inclemente.
Debido a que los sistemas de predicción por conjuntos proporcionan información sobre la incertidumbre, el o los resultados más probables del pronóstico y la distribución de probabilidad de los resultados del pronóstico, los productos operativos de los SPC miden los siguientes aspectos:
- la centralidad y dispersión (para evaluar, en promedio, el resultado más probable y la incertidumbre en el pronóstico)
- la distribución de probabilidad de las predicciones por conjuntos (para evaluar la utilidad de las dos medidas anteriores)
- la probabilidad de exceder umbrales críticos (para evaluar la necesidad de alertas, advertencias, etc.)
Esta sección proporciona información sobre los tipos de productos disponibles actualmente (y otros que están siendo desarrollados) para los SPC, su interpretación y los obstáculos potenciales de su uso.
Productos
Métodos para resumir los datos del conjunto
Los datos del conjunto se pueden presentar en mapas horizontales (por ejemplo, sobre un dominio espacial tal como Norteamérica o el territorio continental de los Estados Unidos, como se muestra en el primer producto) o en diagramas puntuales (es decir, para un lugar en particular, incluyendo sondeos verticales, como se muestra en el segundo producto).
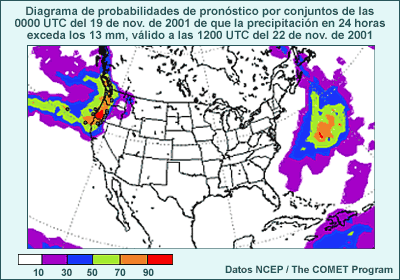
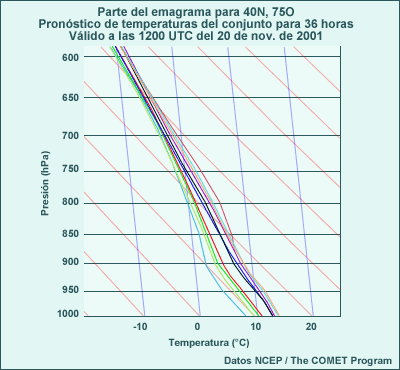
Los productos del conjunto que corresponden a estas categorías se pueden también posprocesar para tomar en consideración las peculiaridades de los modelos que proveen la información. Tales productos han sido calibrados para corregir los errores y asimetrías del modelo en un período fijo del pasado reciente. Describiremos los productos típicos de la predicción por conjuntos en las páginas restantes de esta sección. Al final, veremos también cómo la calibración permite mejorar los productos.
Productos de media y dispersión
La expresión más compacta de la información contenida en un conjunto de pronósticos numéricos es la desviación típica, o la media y dispersión que aparece en mapas o vistas en planta del pronóstico. Recuerde que la información de dispersión de estos mapas supone una distribución normal o gaussiana de los datos del conjunto, o al menos para la población de pronósticos posibles de los cuales se supone que las predicciones por conjuntos son representativos. Existen muchas variables meteorológicas que se prestan a esta clase de presentación, incluyendo, en forma enunciativa, mas no limitativa, las siguientes:
- En la superficie:
- presión al nivel del mar
- temperatura a 2 metros
- vientos a 10 metros
- humedad relativa o específica
- precipitación acumulada
- parámetros de estabilidad
- En superficies de presión constante:
- altura geopotencial
- velocidad del viento
- temperatura del aire
- humedad relativa o específica
El mapa siguiente de la media y la desviación típica del conjunto de pronósticos de 84 horas de alturas de 500 hPa del NCEP para las 0000 UTC del 19 de noviembre de 2001, válidos para las 1200 UTC del 22 de noviembre, ofrece un ejemplo de cómo la media y la dispersión transmiten información compacta. El sombreado representa la desviación típica, mientras que los contornos indican la altura media del conjunto, todo en metros. Compare este mapa con el ejemplo del mapa de 11 miembros del final de la sección anterior, que abarca el mismo dominio, en el cual todos los miembros del conjunto se muestran a intervalos de 100 metros.
.

Pregunta: media y dispersión
Pregunta
Abajo se muestra el mapa de dispersión del conjunto para las alturas a 500 hPa en el hemisferio norte del modelo GFS operativo y de la predicción por conjuntos a mediano plazo (Medium-Range Ensemble Forecast, o MREF) del NCEP ejecutado el 20 de mayo de 2004 y válido el 25 de mayo de 2004 (pronóstico de 120 horas), obtenido del sitio web de MREF. Los contornos muestran la media del conjunto mientras que el sombreado indica la dispersión, de acuerdo con los valores indicados en la escala de colores a la derecha.
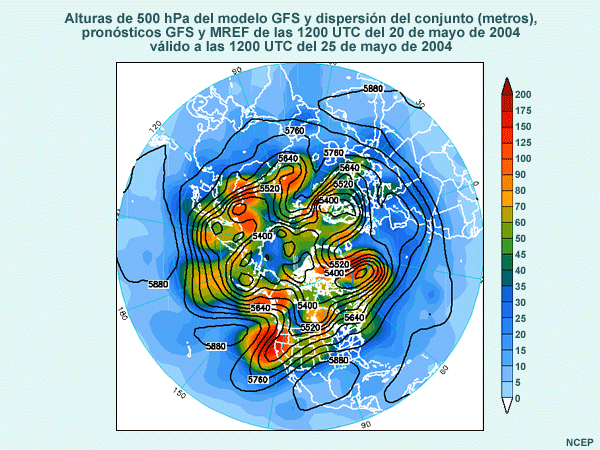
Considerando la dispersión del pronóstico de las alturas a 500 hPa, ¿cuáles de las siguientes afirmaciones sobre el pronóstico del sistema GFS operativo son verdaderas?
Elija todas las opciones pertinentes.
Las respuestas correctas son a), b), y d).
Cuanto mayor sea la dispersión, tanto mayor será la incertidumbre en la predicción por conjuntos. Los colores anaranjado y rojo indican incertidumbre alta y las áreas azules incertidumbre baja. Por tanto, la respuesta a) es correcta. Debido a que la dispersión del área corriente arriba de la vaguada en la región oeste de EE. UU. y de la vaguada misma es alta, la respuesta b) es también correcta. Como solo aparecen los colores azul y azul/verdoso cerca del centro de la baja segregada sobre Escandinavia, por lo tanto la respuesta d) es correcta también. Sin embargo, tanto al norte como al sur de la baja segregada al este del Labrador la dispersión es alta, los indica incertidumbre en su posición latitudinal. Por tanto, la respuesta c) es incorrecta.
Ventajas de la media del conjunto y de la dispersión del pronóstico
Como vimos en el apartado anterior, el mapa de media y dispersión es una buena manera de presentar la información del conjunto en forma compacta. Debido a que la media suaviza las características de pequeña escala relativamente impredictibles presentes en el pronóstico, la verificación es mejor para la media de la predicción por conjuntos que para cualquier miembro individual del conjunto (o para el pronóstico operativo después del tercer día) y deja visibles las características de gran escala, cuyo pronóstico es mejor. Por lo tanto, la media del conjunto proporciona buena información de la evolución más probable de la atmósfera a escalas predictibles. Además, cuanto menor la dispersión del pronóstico, tanto más probable será que la media del conjunto se verifique bien (Toth et al. 2001). Esto significa que una incertidumbre alta en el pronóstico indica también una predictibilidad baja.
Al calcular la dispersión, se pueden también tomar en cuenta regímenes de flujo recientes normalizando la dispersión del pronóstico en uso con respecto al valor medio de un período de pronósticos recientes. Esta dispersión normalizada da la incertidumbre del pronóstico en cada punto de malla en relación con los valores observados recientemente. Los valores mayores que 1 indican que la dispersión es mayor que la media del período considerado, es decir, que hay más incertidumbre de lo «normal». Los valores menores que 1 indican dispersiones con una incertidumbre menor que la media.
El ejemplo que sigue muestra un mapa de la media y la dispersión normalizada del conjunto tomado de la página web del sistema de predicción por conjuntos (SPC) del NCEP para la predicción por conjuntos de las 1200 UTC del 22 de noviembre de 2002, válido para las 1200 UTC del 5 de diciembre de 2002. En la normalización de este gráfico se utilizaron los últimos 30 días y se dio mayor peso a los datos más recientes.
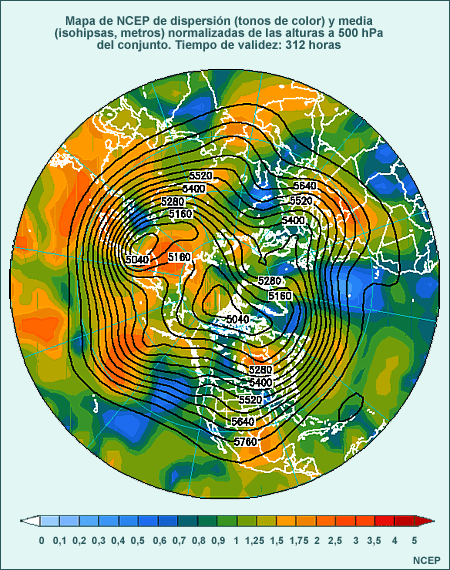
Todos los valores mayores que 1 indican más incertidumbre que durante el período de 30 días, mientras que los valores menores que 1 indican menos incertidumbre en el mismo periodo.
Limitaciones de la media y la dispersión del conjunto
Los cálculos de la media y la desviación típica suponen que los miembros del conjunto tienen una distribución normal, teniendo la media del conjunto la máxima probabilidad de ocurrencia. Sin embargo, la teoría del caos sugiere que en los sistemas físicos como la atmósfera que son sensibles a las condiciones iniciales, son frecuentes las aglomeraciones alrededor de dos o más posibles soluciones del pronóstico. Por consiguiente:
- Si los miembros del conjunto están realmente aglomerados alrededor de dos o más soluciones posibles, tanto la media del conjunto (la solución más probable) como la dispersión (que supone una distribución de datos normal, en forma de campana) pueden ser engañosas.
- La interpretación de la media y la dispersión del conjunto, especialmente cuando el pronóstico sugiere múltiples soluciones probables, requiere información adicional sobre la distribución individual de los miembros del conjunto, como la que brindan los diagramas espagueti. Este es el tema del próximo apartado.
Pregunta: media y dispersión normalizadas
Pregunta
A continuación se muestra la media del conjunto y el diagrama de dispersión normalizado de alturas a 500 hPa, en el hemisferio norte, de la predicción por conjuntos a mediano plazo (Medium-Range Ensemble Forecast, o MREF) del NCEP de las 1200 UTC del 25 de mayo de 2004 válido para las 1200 UTC del 25 de mayo de 2004 (120 horas de pronóstico), obtenido del sitio web de pronósticos por conjuntos del sistema MREF. Las isohipsas indican la media del conjunto mientras que el sombreado indica la dispersión normalizada según la escala de colores a la derecha. Para contestar la pregunta siguiente, necesitará también hacer clic aquí para ver las alturas del modelo operativo GFS y el gráfico de dispersión en bruto del conjunto.
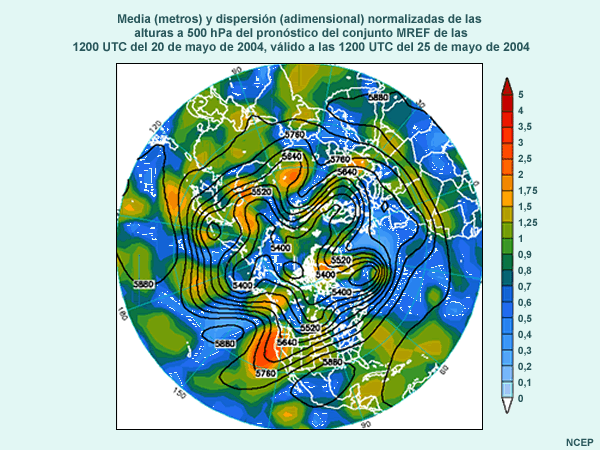
Considerando la media y la dispersión de la predicción por conjuntos de las alturas de 500 hPa que se muestran en el mapa y la dispersión sin procesar, ¿cuáles de las siguientes afirmaciones son ciertas?
Elija todas las opciones pertinentes.
Las respuestas correctas son a), c), y d).
La dispersión normalizada muestra el tamaño relativo de la dispersión del conjunto comparada con la dispersión promedio durante los últimos 30 días. En el gráfico, los colores anaranjados y rojos indican 2 o más, y estos colores se encuentran cerca de la vaguada en el oeste de los Estados Unidos. Por tanto, la respuesta a) es correcta. Si bien la dispersión es relativamente baja sobre el Atlántico, cerca de la costa de Nueva Inglaterra, la dispersión normalizada excede el valor de 1, de modo que la respuesta b) es incorrecta. En el norte de África, pese a que la dispersión es de solamente 30-35 metros, la dispersión normalizada está entre 1 y 1,5 y, por tanto, la respuesta c) es correcta. Finalmente, la dispersión sin procesar para la zona de Quebec, que equivale aproximadamente a la de las opciones b) y c), está en una región donde la dispersión media para los últimos 30 días es más alta, lo cual da una dispersión normalizada en el rango de 0,6 a 0,8. Por tanto, la respuesta d) es correcta.
Diagramas espagueti
Podemos ver todos los miembros del conjunto mediante los diagramas llamados «espagueti». Estos gráficos ofrecen una vista en planta de uno o varios valores de contorno de la variable de interés; esta vista es relativamente sencilla, a la vez que brinda una visión cualitativa de la distribución de las salidas del pronóstico.
En este mapa podemos ver que la isohipsa de 5640 metros para 500 hPa cruza tres áreas de incertidumbre sobre el territorio continental de los EE. UU. El diagrama espagueti que se muestra a continuación corresponde a esa isohipsa. Cada miembro del conjunto se representa con una línea fina de un color diferente, y la media del conjunto se representa con una línea gruesa de color negro.
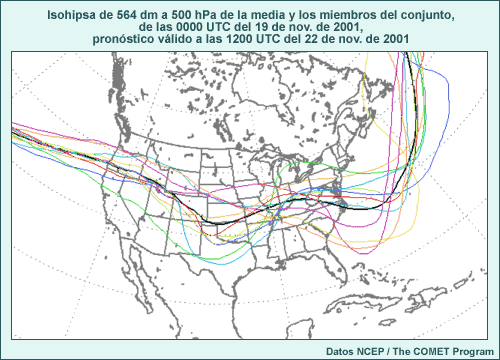
¿Cómo se sabe cuáles isohipsas brindan más información? Los diagramas de media y dispersión nos dan pistas muy útiles. Dado que nos interesa la probabilidad de una variable de pronóstico en regiones en alta incertidumbre, tiene sentido examinar los diagramas espagueti de las isohipsas que cruzan las regiones de máxima incertidumbre. A continuación se muestra el diagrama de media y dispersión generado por el mismo ciclo de ejecución del conjunto y correspondiente al tiempo de validez.

Observe que en el diagrama espagueti (repetido más abajo):
- La isohipsa media del conjunto de 564 dm es más regular que cualquiera de los miembros del conjunto porque las características con menos concordancia se promedian entre los miembros del conjunto.
- La mayor dispersión indicada por el diagrama de media y dispersión frente a la del Atlántico de los EE. UU. y sobre los Grandes Llanos se refleja en la amplia dispersión de la línea de altura de 564 dm, como era esperado.
- Sobre la costa oeste, sin embargo, la dispersión de los contornos es relativamente pequeña a pesar de la alta incertidumbre en el gráfico de media y dispersión. ¿Por qué? Esta área está marcada por un intenso gradiente meridional (de norte a sur) de altura, de modo que los pequeños desplazamientos meridionales en la altura entre un miembro y otro producen grandes dispersiones en los valores de altura. Esto se puede interpretar también como incertidumbre en la posición meridional de los vientos máximos.

Ventajas y limitaciones de los diagramas espagueti
Ventajas:
- Presentación compacta de la información.
- Se muestran todos los miembros del conjunto.
- Podemos tener una idea de la distribución de probabilidad para el pronóstico de los contornos que mostramos.
Desventajas:
- No ofrece un cuadro completo de la distribución de probabilidad del pronóstico.
- Se requiere información adicional para hacer una buena interpretación de los productos, aunque podemos utilizar los diagramas espagueti y los diagramas de media y dispersión de los conjuntos para obtener un mejor cuadro de la distribución de probabilidad del pronóstico conjunto.
Pregunta: diagramas espagueti
Pregunta
El siguiente diagrama espagueti del hemisferio norte muestra las alturas a 500 hPa (para 522 y 564 dm) de la predicción por conjuntos a mediano plazo (Medium-Range Ensemble Forecast, o MREF) del NCEP de las 1200 UTC del 20 de mayo de 2004, válido para las 1200 UTC del 25 de mayo de 2004 (pronóstico de 120 horas), obtenido del sitio web de MREF. La línea negra representa la media del conjunto, la línea gris es el Sistema de Pronóstico Global (Global Forecast System, o GFS) operativo y los miembros del conjunto se muestran con líneas finas de diferentes colores. Resulta útil también ver las alturas del sistema GFS operativo y el gráfico de dispersión de los datos no procesados del conjunto (haga clic aquí).
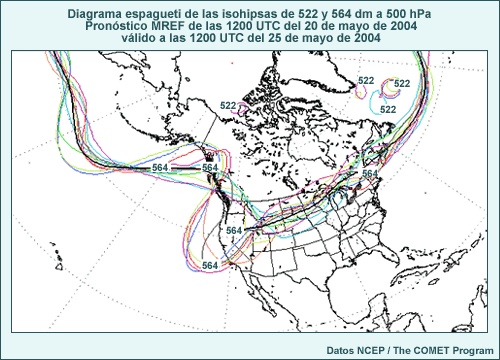
Considerando el diagrama espagueti anterior, ¿cuáles de las siguientes afirmaciones son ciertas?
Elija todas las opciones pertinentes.
Las respuestas correctas son b) y d).
Los diagramas espagueti muestran uno o algunos contornos de un campo de interés para destacar las distribuciones de probabilidad de una variable en regiones de interés. Las opciones se concentran en los contornos de la isohipsa de 564 dm sobre el oeste de los EE. UU. Las líneas han formado dos grupos significativos: uno para una vaguada más profunda y de evolución más lenta que la media y otro para una vaguada más rápida y débil ubicada considerablemente más al este. Un miembro del conjunto, en color naranja, se desvía más de la media que los demás, mientras la media del conjunto se halla entre los dos grupos que representan los dos resultados más probables del pronóstico. La aglomeración en dos soluciones indica que el pronóstico medio del conjunto no representa el resultado más probable del pronóstico y que los miembros del conjunto tienen una distribución más bien bimodal que normal. Por consiguiente, la respuesta b) es correcta y las respuestas a) y c) son incorrectas.
Podemos utilizar los diagramas de media y dispersión para determinar las regiones y las isohipsas que conviene examinar. Si consideramos los mapas anteriores, la isohipsa de 564 dm tiene mucha dispersión (tanto en términos absolutos como en términos normalizados) fuera de la costa oeste de los EE. UU. y dentro de la región intermontana en el oeste del país. Por lo tanto, la respuesta d) es correcta.
Diagramas de los eventos más probables
Otra forma de representar en planta la información del conjunto muestra los resultados más probables de la predicción por conjuntos. Una variable muy adecuada para esta presentación es el tipo de precipitación. El siguiente ejemplo de este tipo de gráfico fue tomado del sitio web de predicción por conjuntos a corto plazo (Short-Range Ensemble Forecast, o SREF) del NCEP. Este mapa muestra el o los tipos dominantes de precipitación (que se definen como los tipos que ocurren con mayor frecuencia entre los miembros del conjunto que presentan precipitación) del pronóstico de las 1200 UTC del 12 de noviembre de 2002, válido para las 0000 UTC del 15 de noviembre de 2002. El tipo de precipitación en el SREF se determina usando el algoritmo de Baldwin-Schichtel. Si ninguno de los miembros predice precipitación, el punto de malla aparece en blanco. Si hay varios tipos de precipitación dominante con el mismo valor, se pronostica una mezcla de tipos.
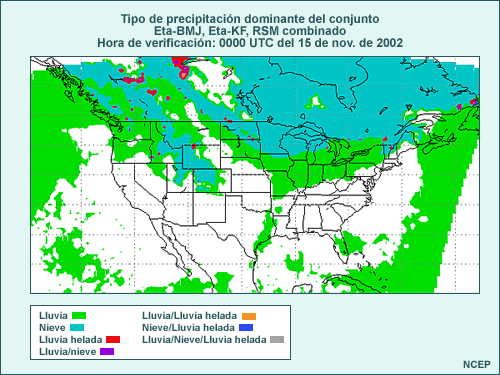
Ventajas y limitaciones de los gráficos de pronóstico más probable
Ventajas:
- Presentación compacta.
- Indican cuál es la salida más probable de la predicción por conjuntos.
Desventajas:
- Pueden ocultar otras salidas de pronóstico cuya probabilidad es casi igual.
- Las salidas de pronóstico «más probables» pueden no haber sido producidas por la mayoría de los miembros del conjunto. Por ejemplo, si cinco miembros del conjunto predicen nieve, cuatro lluvia congelada, tres lluvia y tres granizo como tipo de precipitación en un ciclo de ejecución de 15 miembros de un SPC, se indicará nieve como la precipitación más probable, pese a que ocurre en solo el 33 % de los casos.
Probabilidad de exceder un valor
La función del pronosticador es predecir los eventos de clima violento o severo. Los productos del conjunto que indican la probabilidad de exceder un valor pronosticado nos ayudan en esta tarea. La probabilidad de exceder un valor se calcula dividiendo el número de miembros del conjunto que exceden el umbral elegido entre el número total de miembros del conjunto.
Por ejemplo, el primero de los dos mapas siguientes muestra la probabilidad de que la cantidad de precipitación en 24 horas exceda 13 mm, a las 0000 UTC del 19 de noviembre de 2001, para el período que termina a las 1200 UTC del 22 de noviembre de 2001. El diagrama espagueti de precipitación acumulada en exceso de 13 mm en 24 horas para cada miembro del conjunto se muestra en el segundo mapa.


Umbrales variables para la probabilidad de exceder un valor
A veces, el umbral de interés depende de la situación del momento. Por ejemplo, la cantidad de precipitación que dará lugar a crecidas repentinas depende en parte de las condiciones actuales del suelo. Un producto experimental de la predicción por conjuntos producido por el Centro de Predicción Hidrometeorológica (Hydrometeorological Prediction Center, o WPC) del NCEP es la guía probabilística de crecidas repentinas, un ejemplo del cual puede verse abajo. Este producto se crea a partir de la predicción por conjuntos a corto plazo (Short-Range Ensemble Forecast, o SREF).
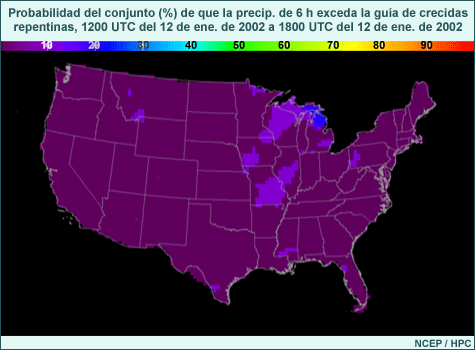
La escala de colores de la parte superior del mapa indica la probabilidad determinada por el conjunto de que la precipitación de 6 horas exceda el valor local de la guía de crecidas repentinas durante el período que termina a las 1800 UTC del 12 de enero de 2002.
Otros gráficos de probabilidad pueden mostrar el valor pronosticado por el conjunto de una variable en un umbral fijo de probabilidad; por ejemplo, la cantidad de precipitación con un 60 % de probabilidad de ocurrencia en el conjunto.
Ventajas y limitaciones de los gráficos de probabilidad de exceder un valor
Ventajas:
- Presentación compacta.
- Se centra en umbrales importantes de variables de pronóstico críticas.
Desventajas:
- Solo muestran una parte de la distribución de probabilidad del pronóstico en lugar de la distribución total y, como resultado, no muestran directamente el grado de incertidumbre de la predicción por conjuntos.
- Pueden ocultar soluciones menos probables que, de ocurrir, tendrían un gran impacto en la zona.
Pregunta: probabilidad de exceder un valor
Pregunta
Abajo encontrará el diagrama de probabilidad de exceder un índice de temperatura-humedad, o ITH (que también se conoce por la sigla THI del inglés) mayor que 26,5 °C (80 °F) de la predicción por conjuntos a corto plazo (Short-Range Ensemble Forecast, o SREF) del NCEP de las 0900 UTC del 21 de mayo de 2004 válido para las 2100 UTC del 22 de mayo de 2004. Las probabilidades se muestran en deciles según los valores indicados por la escala de colores debajo del mapa.
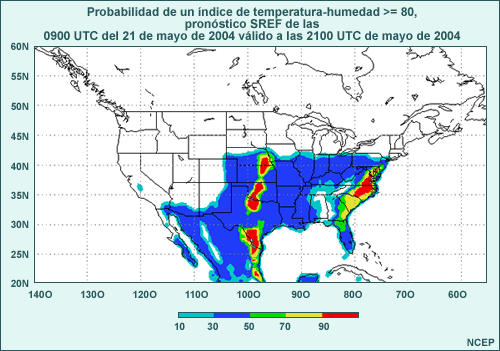
Suponiendo que se debe emitir una advertencia de calor si existe una probabilidad del 60 % o más de que el ITH sea igual o mayor que 26,5 °C, ¿cuáles de las afirmaciones siguientes son ciertas?
Elija todas las opciones pertinentes.
Las respuestas correctas son b) y c).
Los diagramas de probabilidad de exceso nos ayudan en la evaluación de eventos extremos. En este caso, estamos evaluando el exceso de calor. Si el criterio para emitir una advertencia de calor es una probabilidad del 60 % de exceder un ITH de 26,5 °C, entonces será preciso emitir advertencias para las áreas del mapa en rojo (más del 90 %), amarillo (más del 70 %) y la mitad superior del verde (más del 50 %). El mapa muestra que los estados de Alabama y Misisipí no cumplen con el criterio y que la mayor parte del sudeste de los Apalaches, el sur y norte central de Texas, el oeste central de Oklahoma y el noreste de Kansas sí cumplen con el criterio de advertencia de calor. Por consiguiente, las respuestas a) y d) son incorrectas, mientras que b) y c) son correctas.
Diagramas puntuales
Para representar pronósticos por conjuntos de un punto o, mejor dicho, una celda de malla, los datos se suelen trazar como series temporales. Hay dos tipos generales de diagramas:
- Diagramas de abanico, que muestran la evolución temporal de una variable de pronóstico para cada miembro del conjunto, más la media del conjunto (equivalentes a los diagramas espagueti en planta).
- Diagramas de cajas y bigotes, que muestran la media del conjunto y la dispersión de una variable de pronóstico en forma de cajas y bigotes que indican, respectivamente, los percentiles y los extremos. Este es el equivalente puntual de un mapa espacial de media y dispersión.
Aunque también se pueden representar los sondeos del conjunto, que muestran la estructura vertical media de temperatura y humedad de cada miembro para una celda de la malla, por simplicidad normalmente solo se muestran para momentos discretos.
Diagramas de abanico
Este ejemplo de un diagrama de abanico muestra los resultados del ciclo ejecutado a las 0000 UTC del 19 de noviembre de 2001. Hemos elegido un punto en 40°N y 75°O para ilustrar los productos. Este diagrama muestra la temperatura en el nivel de 2 metros generada por cada miembro de la predicción por conjuntos a intervalos de 12 horas hasta las 1200 UTC del 22 de noviembre.
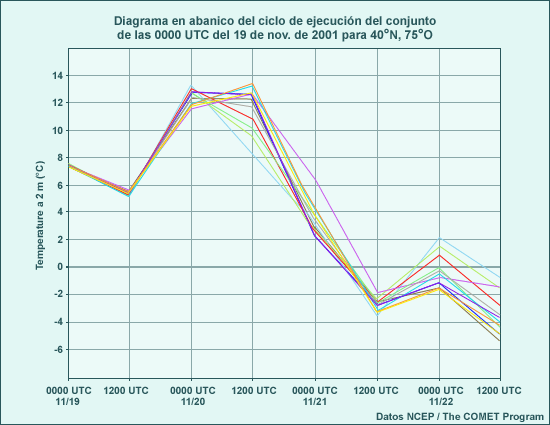
Observe que las diferencias de temperatura entre los miembros del conjunto, aumentan con el tiempo hasta alcanzar un rango de 5 °C en 36 horas (1200 UTC del 20 de noviembre). Observe también que puede haber valores atípicos y aglomeraciones, como en los mapas espaciales con los diagramas tipo espagueti. Este diagrama se puede utilizar junto con los gráficos de vista en planta obtenidos del conjunto para asociar las series temporales de los diagramas de abanico con diferentes situaciones de escala sinóptica en la predicción por conjuntos. Por ejemplo, la curva con los valores más altos (violeta claro) del diagrama de abanico anterior pertenece a un miembro del conjunto que desarrolló una progresión mucho más lenta de un frente frío a través del punto de interés. Por otra parte, la curva más fría después de 36 horas (celeste) es la de un miembro del conjunto que generó una progresión más rápida del mismo frente debido a efectos de advección fría y radiación más pronunciados producto de cielos más despejados, en relación con los otros miembros del conjunto.
Pregunta: diagramas de abanico
Pregunta
Este diagrama de abanico de la predicción por conjuntos a mediano plazo para 8 días de las temperaturas a 2 metros a partir de las 1200 UTC del 24 de mayo de 2004 corresponde a una celda de malla próxima a Washington, DC. Los datos se presentan en intervalos de seis horas (0000, 0600, 1200 y 1800 UTC). La línea negra representa la media del conjunto y las líneas de colores representan los otros miembros del conjunto. Las marcas en el eje de tiempo representan las 0000 UTC de la fecha indicada.
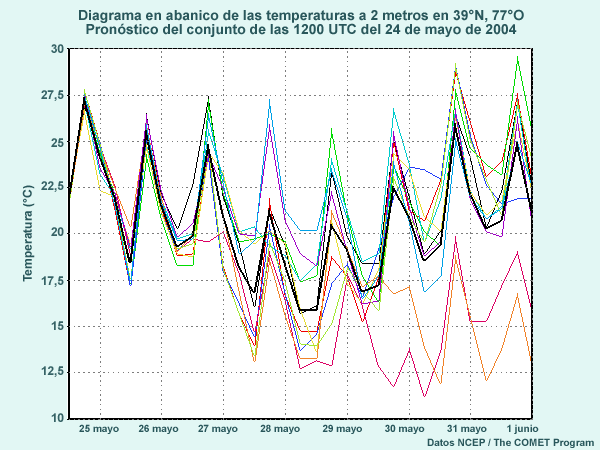
Después de estudiar el diagrama de abanico, ¿cuál de las opciones siguientes es la correcta? Escoja la mejor respuesta.
La respuesta correcta es b)
La interpretación de un diagrama de abanico es similar a la de un diagrama tipo espagueti. Puede haber múltiples aglomeraciones de probables resultados de pronóstico, la distribución de probabilidad puede inferirse de la posición de los miembros individuales del conjunto y el valor medio del conjunto puede o no ser representativo de la solución más probable, dependiendo de la naturaleza de la distribución de los datos (normal, bimodal o multimodal). En este caso, hay una fuerte tendencia de agrupamiento alrededor de soluciones diferentes para la temperatura del nivel de 2 m, especialmente entre el 27 y 28 y el 30 y 31 de mayo. Hay una minoría de miembros cálidos entre el 27 y 28 de mayo y de miembros fríos entre el 30 y 31 de mayo. Debido a la aglomeración, la respuesta b) es correcta y a) es incorrecta. Debido a la distribución, podemos ver que la temperatura más probable para el nivel de 2 m el 31 de mayo podría ser más cálida de lo indicado por la media del conjunto.
Los diagramas de abanico también permiten detectar tendencias. Hay una tendencia media hacia el enfriamiento el 24-28 de mayo y un calentamiento subsiguiente. Por lo tanto, las respuestas c) y d) son incorrectas.
Diagramas de cajas y bigotes
El diagrama de cajas y bigotes que aparece a continuación corresponde a los datos de la sección anterior. Los bigotes se extienden por encima y por debajo de las cajas hasta los valores extremos de los miembros del conjunto, mientras que los valores de los lados de arriba y de abajo de las cajas indican los valores superior e inferior de los dos cuartiles centrales (el rango de los datos ordenados entre el 25 y el 75 %). La mediana de la temperatura está representada por un círculo rojo.

Observe que la mediana no está siempre en la mitad de la caja. Cuando la mediana está desplazada del centro de la caja, indica que los miembros del conjunto no están distribuidos simétricamente (por ejemplo, pueden ser asimétricos). Por ejemplo, podemos ver que a las 1200 UTC del 20 de noviembre de 2001 la mediana tiene casi el mismo valor que el percentil 75. Esto concuerda bien con el diagrama de abanico anterior, donde siete de los miembros del conjunto de una de las aglomeraciones tienden hacia el calor (de ellos, tres tienen la misma temperatura), mientras que cuatro son considerablemente más fríos, pero más dispersos que los del grupo cálido.
Observe también que el diagrama de cajas y bigotes nos da poca información sobre la media del conjunto. Este diagrama representa directamente solo la mediana y los cuartiles, que no se refieren a promedios, sino a datos ordenados.
Pregunta: diagramas de cajas y bigotes
Pregunta
Este diagrama de cajas y bigotes para la celda de malla próxima a Washington, DC muestra la predicción por conjuntos de plazo medio de las temperaturas del nivel de 2 m de las 1200 UTC del 24 de mayo de 2004, para los días 1 a 8. Los datos graficados son los mismos que para la pregunta sobre el diagrama de abanico y se presentan en intervalos de seis horas (0000, 0600, 1200 y 1800 UTC). Las cajas representan los dos cuartiles centrales, los extremos de los bigotes representan los valores extremos y las rayas horizontales representan la mediana. Las marcas del eje de tiempo representan las 0000 UTC de la fecha indicada.
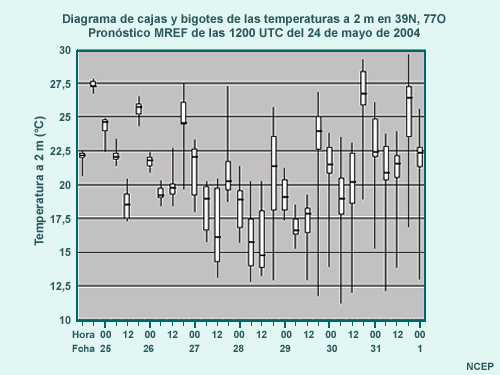
Elija la mejor respuesta.
La respuesta correcta es d)
El diagrama de cajas y bigotes muestra rangos de cuartiles, medianas y valores extremos. Las cajas representan los dos cuartiles del medio, separados por la mediana, mientras que las líneas verticales o rayas, muestran los valores extremos. Con respecto a la opción a), el rango dado de 1,5 °C es el de los dos cuartiles del medio, no el rango completo del valor mínimo al valor máximo. Por consiguiente, esta opción es incorrecta. La mediana es un valor único, no un rango de valores; de modo que la opción b) es también incorrecta. El valor de 17 °C en la opción c) es el valor inferior del cuartil 2, no el valor mínimo, así que la opción c) es incorrecta. La caja de las 1200 UTC del 27 de mayo de 2004 muestra un rango entre 14 y 19,5 °C. Puesto que la caja indica los dos cuartiles centrales de los datos del conjunto, la opción d) es correcta.
Sondeos del conjunto
Los sondeos del conjunto se usan para mostrar el grado de incertidumbre en la estructura vertical de la temperatura y/o la estructura de humedad para una columna del modelo. Para ilustrar esto utilizaremos la columna centrada en 40N y 75O, el mismo lugar que los gráficos anteriores. La gráfica siguiente muestra los pronósticos de temperatura, de 1000 a 600 hPa, de los miembros del conjunto válidos para las 1200 UTC del 20 de noviembre de 2001. El código de colores de los miembros del conjunto es el mismo usado en el diagrama de abanico de la sección «Diagramas puntuales».

Observe que la curva de temperatura más fría del nivel de 2 m que en el diagrama de abanico anterior aparece como atípica, también aparece más fría en la estructura vertical de temperatura en la troposfera baja y media.
Ajuste de la asimetría
Normalmente, el posprocesamiento de los resultados de las predicciones por conjuntos supone ajustar las estadísticas del conjunto para tomar en cuenta las asimetrías y los errores sistemáticos de la predicción por conjuntos dentro de un período de «entrenamiento» (este procedimiento no elimina el error aleatorio, que es lo que pretende aprovechar la incertidumbre de la predicción por conjuntos). La duración del período de entrenamiento varía según el propósito del ajuste. Para períodos cortos (del orden de un mes), se tomará en cuenta el régimen más reciente, que afectará al tamaño y la posición de las asimetrías del modelo. Para los períodos más largo (por ejemplo, una o más estaciones completas de diferentes años), las tendencias y los errores del modelo serán más independientes de un régimen específico.
En las secciones siguientes examinaremos dos productos de la sección de modelación del clima y tiempo global (Global Climate and Weather Modeling Branch) del NCEP, uno aplicado a los campos de masa (alturas) y el otro a la parametrización física (precipitación). A continuación veremos cómo se aplica la corrección de la asimetría a un producto usado por el Centro de Predicción Climática (Climate Prediction Center, o CPC) del NCEP en su pronóstico de 6 a 10 días y de dos semanas.
Medida relativa de predictibilidad
¿Cómo podemos cuantificar la información de los conjuntos sobre la predictibilidad de un régimen de flujo en particular o la variabilidad de la predictibilidad en diversas épocas del año? La medida relativa de predictibilidad (Relative Measure of Predictability, o RMOP) es una herramienta que trata de cuantificar esta información.
Teoría de la medida relativa de predictibilidad
Considere el diagrama siguiente, que ilustra las distribuciones de probabilidad de ciclos de ejecución hipotéticos de conjuntos con bajos y altos grados de incertidumbre en un punto de malla del modelo junto con la distribución de probabilidad climatológica para ese punto, indicada por las columnas negras abiertas que marcan una frecuencia relativa del 10 %. La línea horizontal marca la probabilidad climatológica (el 10 %) de que un miembro del conjunto esté en una clase, mientras que las columnas rojas y azules indican el porcentaje de los miembros del conjunto que pertenecen a los conjuntos con incertidumbre pequeña y grande, respectivamente, que caen en cada grupo climatológico. La media del conjunto para cada distribución hipotética se grafica con una línea vertical gruesa codificada con un color.
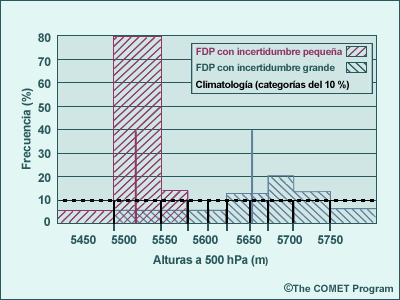
Algunos estudios han demostrado que cuando muchos miembros de un conjunto caen en la misma clase climatológica, la atmósfera es intrínsecamente más predictible que cuando están distribuidos en varias clases. Podemos utilizar este hecho para cuantificar la «predictibilidad relativa» de la atmósfera en cada punto de malla de la predicción por conjuntos, comparando la distribución del ciclo de ejecución del conjunto actual de una variable de pronóstico, por ejemplo la altura a 500 hPa, con la de un período del pasado.
Aplicación de la teoría de la medida relativa de predictibilidad
El sistema de predicción por conjuntos del NCEP usa el período más reciente de pronósticos por conjunto de 30 días y el número de miembros del conjunto que cae en la misma clase climatológica que el pronóstico medio del conjunto como una medida de la predictibilidad atmosférica. En el producto de medida relativa de predictibilidad (RMOP, por sus siglas en inglés), se da más peso a las predicciones por conjuntos más recientes. De esta manera, se acentúa el desempeño del modelo después de cualquier cambio reciente en el régimen de flujo.
Para ilustrar el uso de la medida relativa de predictibilidad, considere el mapa siguiente, que muestra la medida relativa de predictibilidad (sombreado) y el pronóstico del conjunto de la altura media en el nivel de 500 hPa (isohipsas) a las 0000 UTC del 11 de octubre de 2001, válido para las 0000 UTC del 17 de octubre de 2001 (pronóstico de 144 horas).
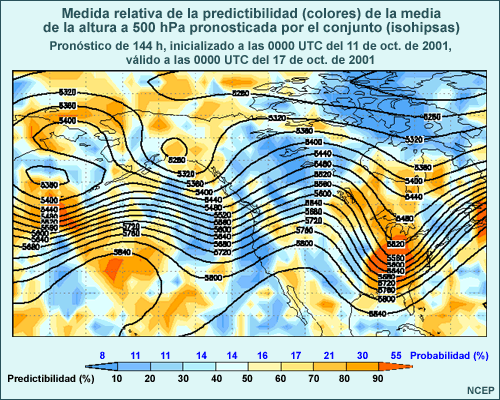
La medida relativa de predictibilidad se da en incrementos del 10 %, tal como lo indican los números en negro debajo de la escala de colores del mapa; observe que aquí el 10 % no está relacionado con las 10 categorías climatológicas igualmente probables. El sombreado del 90 % indica que durante los últimos 30 días, la atmósfera en ese punto fue menos predictible el 90 % del tiempo. Es decir, el 90 % del tiempo menos miembros del conjunto cayeron en la misma categoría que la media del conjunto. Por consiguiente, en este caso la porción de la vaguada sombreada en naranja en el este de los EE. UU. es un 90 % menos predictible en relación a las predicciones por conjuntos del período de 30 días.
Los números en azul sobre cada segmento de la escala de colores debajo del mapa representan el porcentaje del tiempo que en los últimos 30 días la media de la predicción por conjuntos se verificó cuando el pronóstico tenía el grado de predictibilidad indicado por el sombreado. En este caso, el número sobre el segmento de predictibilidad del 90 % indica que solo el 55 % de los pronósticos con un 90 % de predictibilidad relativa en 144 horas dieron resultados adecuados de verificación. Cabe observar que, en términos generales, podemos esperar que la probabilidad de la verificación disminuya:
- a medida que aumenta el tiempo de pronóstico;
- durante la estación cálida; y
- durante regímenes relativamente impredictibles, en cualquier estación.
Pregunta: medida relativa de predictibilidad
Pregunta
Abajo encontrará un ejemplo de un diagrama operativo de medida relativa de predictibilidad del NCEP que representa los pronósticos de alturas a 500 hPa de 144 horas del hemisferio norte de la predicción por conjuntos a mediano plazo (Medium-Range Ensemble Forecast, o MREF) de las 0000 UTC del 20 de mayo de 2004, válido para las 0000 UTC del 26 de mayo de 2004. Las isohipsas representan la media del conjunto, mientras que la medida relativa de predictibilidad está sombreada, de acuerdo con los valores de predictibilidad indicados en negro y la probabilidad de verificación indicada en azul en la escala de colores. Para contestar la pregunta de abajo, es posible que también necesite ver el gráfico de alturas del modelo GFS y las dispersiones no procesadas del conjunto y el gráfico de la media y dispersión normalizada del conjunto para la predicción por conjuntos de las 1200 UTC del 20 de mayo de 2004 válido para las 1200 UTC del 25 de mayo de 2004. (NOTA: los diagramas de medida relativa de predictibilidad se producen solamente para los ciclos de las 0000 UTC, pero se pueden aplicar a pasadas del conjunto próximas en el tiempo).
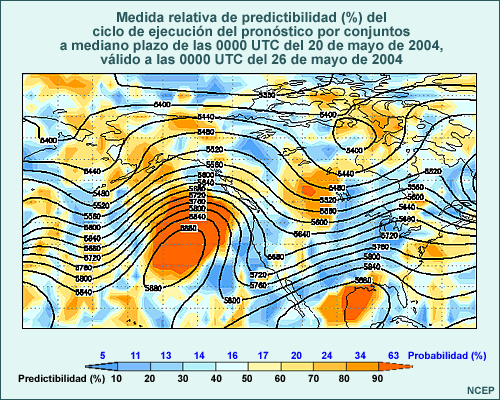
Después de examinar el diagrama de medida relativa de predictibilidad y los gráficos de los enlaces, considere las respuestas siguientes y elija todas las que sean pertinentes.
Las respuestas correctas son a), b) y c).
El diagrama de medida relativa de predictibilidad muestra la predictibilidad y la probabilidad de verificación para la media de la predicción por conjuntos, así como las isohipsas de la media del conjunto, con base en el desempeño del sistema de conjuntos en los últimos 30 días. En el mapa, la parte sombreada en rojo indica una predictibilidad del 90 %, pero con un 63 % de probabilidad de verificación. Las partes sombreadas en azul son predictibles en menos del 50 %, con un 16 % de probabilidad de verificación o menos. Las respuestas (b) y (c) son por tanto correctas, mientras que la respuesta (d) es incorrecta.
Un examen de los otros gráficos de dispersión del conjunto indica alta dispersión en el oeste de los EE. UU. y baja dispersión (en sentido relativo) en el Pacífico Este. Estos resultados muestran una correlación negativa con la predictibilidad en el diagrama anterior. Por consiguiente, la respuesta a) es correcta.
Otros pronósticos por conjuntos calibrados
Otros pronósticos por conjuntos calibrados
La media y dispersión del conjunto y la probabilidad de exceder un umbral se pueden calibrar con el desempeño reciente del sistema de predicción por conjuntos. El mapa siguiente muestra un ejemplo para la precipitación en 24 horas tomado del sitio web de verificación del NCEP. Se muestran las probabilidades no calibradas (izquierda) y calibradas (derecha) de que la precipitación en 24 horas exceda los 13 mm el día 5 de una predicción por conjuntos de las 0000 UTC del 01 de noviembre de 2002. La escala de colores debajo del mapa muestra los intervalos de probabilidad. Los contornos negros marcan intervalos del 30 % a partir del 5 % de probabilidad. Para hacer la calibración, se tomó en cuenta la asimetría en la distribución de probabilidad para la precipitación en cada celda de la malla durante los últimos 30 días, dando más peso a los datos más recientes, de forma similar al procedimiento de ponderación de la medida relativa de predictibilidad que describimos en la sección anterior.
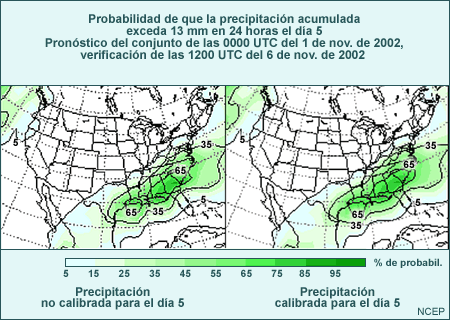
Las diferencias son sutiles pero notorias en el sudeste de los EE. UU., con una ligera expansión del área con mayores probabilidades de recibir más de 13 mm de precipitación en 24 horas en la versión calibrada.
El Centro de Predicción Climática (Climate Prediction Center, o CPC) del NCEP también vigila el desempeño de los modelos SPC y GFS para cierto número de variables de pronóstico pertinentes a los pronósticos de 6 a 10 días y de 2 semanas. Abajo se muestra un ejemplo de pronóstico del GFS de 6 a 10 días para la temperatura en el nivel de 850 hPa de las 0000 UTC del 15 de noviembre de 2002. Se muestran las correcciones del pronóstico para la temperatura de 6 a 10 días usando las asimetrías de los períodos de pronóstico de 7 y de 30 días anteriores.
Temperatura en el nivel de 850 hPa, días 6 a 10 del pronóstico usando las condiciones iniciales del 15 de noviembre de 2002
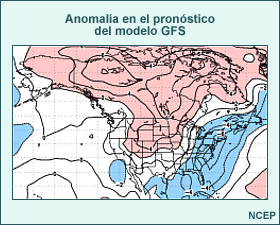
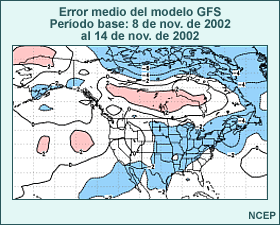
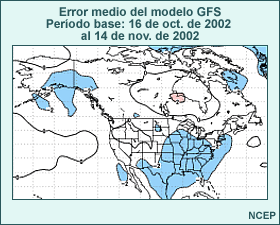
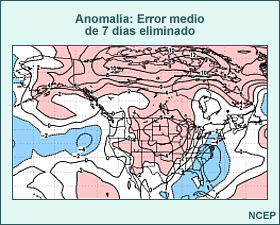
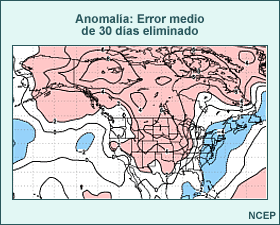
Observe que la tendencia al frío sobre los EE. UU., al este de las Montañas Rocosas, en los períodos anteriores de 7 y de 30 días producen una reducción de la anomalía fría pronosticada por el modelo GFS en esa zona para el período de pronóstico de 6 a 10 días. Si bien esta calibración se aplica al pronóstico de GFS de mediano plazo, el mismo método de calibración se puede aplicar a la media de las predicciones por conjuntos del SPC.
Interpretación de los productos
Interpretación de la media y dispersión con diagramas espagueti
Sugerencia 1: Una dispersión grande en una característica producida por la media del conjunto significa incertidumbre en la amplitud de la característica.
En esta ilustración, las áreas sombreadas muestran que la incertidumbre se halla principalmente en la distribución vertical de los contornos de las medias del conjunto, tal como se puede apreciar en el diagrama espagueti adjunto. Aunque debemos considerar la probable existencia de una vaguada, cabe dudar que la media haya capturado el grado de intensidad probable. Si hubiera duda sobre la existencia de la característica, la media del conjunto probablemente mostraría una amplitud de onda pequeña y un sombreado intenso en ese lugar, sugiriendo la presencia de miembros del conjunto con dorsales y vaguadas.
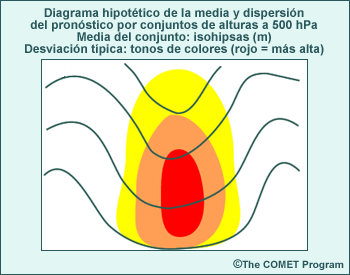
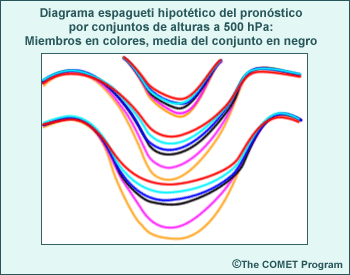
Sugerencia 2: Grandes dispersiones corriente arriba y corriente abajo de una característica producida por la media del conjunto significan incertidumbre en la ubicación de la característica.
Como se ve en la ilustración siguiente, la presencia de dos áreas de incertidumbre a los lados de la característica de la media del conjunto significa que el conjunto presenta dudas en cuanto al tiempo y el lugar. También en este caso la existencia de la característica es relativamente segura. Observe que en el diagrama espagueti, la mayor dispersión de las isohipsas está corriente arriba y corriente abajo del pronóstico de la media del conjunto para el eje de la vaguada en el nivel de 500 hPa.
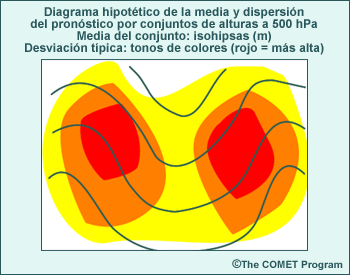
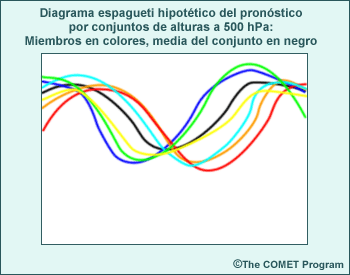
Sugerencia 3: Una dispersión asimétrica grande en relación con una característica producida por la media del conjunto significa que el aglomerado de una minoría de posibles soluciones del pronóstico difiere de la media del conjunto.
Esta configuración se muestra en la primera ilustración. El diagrama espagueti correspondiente para algunas isohipsas del nivel de 500 hPa se muestra en la segunda ilustración. Observe el aglomerado de pronósticos (la zona coloreada) con la profunda vaguada de onda corta corriente abajo del eje de vaguada de la media del conjunto, la cual parece ser una característica exclusiva de estos miembros del conjunto.
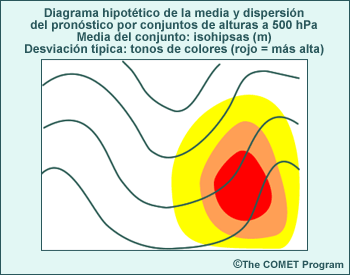
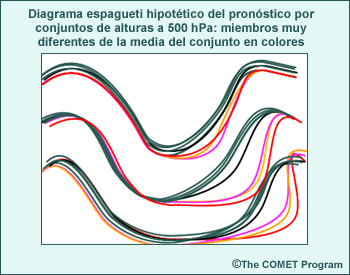
Sugerencia 4: Como muestra cada uno de los ejemplos anteriores, a menudo resulta útil examinar los diagramas espagueti para entender mejor los diagramas de media y dispersión.
Interpretación de la media y dispersión en los productos de precipitación con diagramas espagueti
A menudo, las cantidades de precipitación acumuladas en los rangos de tiempo típicos de los pronósticos de corto y mediano plazo no presentan una distribución normal. Esto complica en cierta medida la interpretación de los productos de media y dispersión de la precipitación en comparación con otros valores. Sin embargo, la sugerencia y el ejercicio siguientes le mostrarán estrategias para usar dichos productos.
Sugerencia 1: Una gran dispersión en la cantidad de la precipitación, aún con una media del conjunto relativamente pequeña, puede ser una indicación de un potencial evento de precipitación extrema.
Considere el siguiente gráfico idealizado de la dispersión y media del conjunto para la precipitación de 12 horas sobre un área de pronóstico hipotética, producto de una predicción por conjuntos con 11 miembros. Las isohietas indican la precipitación media del conjunto (se muestran las de 0,25, 2,5, 6,5 y 13 mm), mientras que las áreas sombreadas muestran la dispersión de acuerdo con la escala de colores.
Pregunta
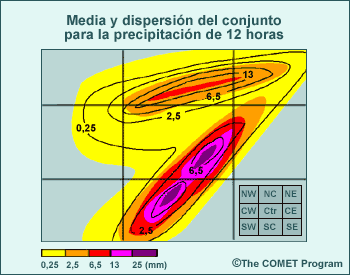
Dada la media y dispersión de los campos de precipitación y el mismo umbral crítico de crecida repentina para toda la región de 36 mm en 12 horas, ¿dónde es mayor la posibilidad de una crecida repentina? El área está dividida en seis regiones por las líneas grises, las cuales se denominan con base a su ubicación según el recuadro abajo a la derecha del gráfico.
La respuesta correcta es c)
Esto es cierto pese a que la precipitación media del conjunto es mayor en la región norte central. La clave está en interpretar la dispersión de la precipitación en vez de confiar solo en la media del conjunto.
Una dispersión mayor que la media del conjunto en un mapa de media y dispersión de la precipitación sugiere que la mayor parte de los miembros del conjunto generan menos precipitación, pero que también algunos de ellos producen mucha más precipitación que la media del conjunto, es decir, existe el potencial para un evento de precipitación extrema. Los patrones de media y dispersión de este tipo son típicos de los pronósticos de precipitación por conjuntos de la estación cálida, cuando la precipitación convectiva es dominante tanto en la naturaleza como en las formulaciones de los modelos de PNT.
En el ejemplo anterior, tenemos dos áreas bien diferenciadas en las cuales la precipitación media del conjunto está entre 6,5 y 13 mm, pero la dispersión excede los 25 mm solo en las regiones central y sur central, indicando que una crecida repentina es una posibilidad allí. Si consideramos además los problemas inherentes a los modelos de PNT para determinar el momento y el lugar del inicio de la convección y las cantidades de precipitación, la interpretación se vuelve aún más complicada. Esta complicación adicional se ilustra para el mismo caso hipotético usando el diagrama espagueti de umbral crítico de precipitación (36 mm) para 12 horas generado como orientación para las crecidas repentinas. El pronóstico de cada miembro del conjunto se muestra en un color diferente.
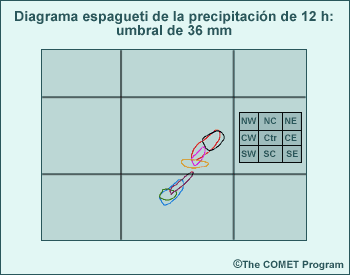
Esto nos permite formular la
Sugerencia 2: Los diagramas espagueti para los umbrales críticos de precipitación pueden ser útiles en la interpretación de la media y dispersión de los productos de precipitación.
Podemos ver que 7 de los 11 miembros del conjunto exceden el umbral crítico de precipitación en las regiones SC y Ctr, mientras que ninguno de los miembros del conjunto lo excede en el área NC, donde la precipitación media del conjunto era más alta. Este resultado es bastante razonable porque:
- En una celda de la malla con una media de 10 mm de lluvia en 12 horas pero con una dispersión mayor a 25 mm puede haber al menos dos miembros cuya precipitación de 12 horas excede el umbral de precipitación para una crecida repentina.
- En una celda de la malla con una precipitación media superior a 13 mm, pero con una dispersión de un poco más de 6,5 mm es fácil que todos los miembros del conjunto estén por debajo del umbral para una crecida repentina.
Una interpretación posible es que hay un riesgo del 63 % de exceder el umbral de crecida repentina en algún lugar de las regiones afectadas. En este caso, si no tenemos en cuenta la dispersión de la precipitación, la cantidad de precipitación media del conjunto puede llevarnos a una interpretación equivocada.
Escala de las características en las predicciones por conjuntos
Los sistemas de previsión por conjuntos, o SPC, se ejecutan a una resolución más tosca (menor) que los modelos operativos válidos para el mismo período. La escala de las características en los pronósticos por conjunto a mediano plazo (3 a 7 días) varía con la predictibilidad del régimen. En general, se pueden seguir estas reglas con respecto a la escala del pronóstico de características a mediano plazo:
- Las características de gran escala (que son fáciles de predecir y representar con una
resolución baja) tenderán a ser mejor pronosticadas.
- La predictibilidad de estas características dependerá del régimen del flujo y de la época del año (por ejemplo, la predictibilidad fría es mejor durante la estación fría que durante la estación cálida).
- Los patrones en gran escala de la media del conjunto, que se asemejan a características persistentes forzadas por la variabilidad en la gran escala (por ejemplo, El Niño, las oscilaciones Madden-Julian, etc.), tienen una mayor confianza de verificación.
El siguiente es un buen ejemplo de estos puntos. El primer mapa muestra un pronóstico de la media del conjunto de 144 horas para la altura de 500 hPa (y la medida relativa de predictibilidad) y el segundo muestra un pronóstico de 24 horas válido para el mismo período. Cuando se hicieron estos pronósticos, estaba en curso un evento moderado de El Niño (o «evento cálido») en el Pacífico ecuatorial central.
Primero, observe la dorsal en el oeste de Norteamérica y la vaguada en el este de Norteamérica, una configuración típica durante un evento cálido moderado. Segundo, observe los detalles que aparecen en el pronóstico de 24 horas, como la vaguada de onda corta en la región central de Canadá, que no aparecen en el pronóstico de 144 horas, lo cual ilustra el suavizado producido sobre la media del conjunto de rangos de tiempo mayores.
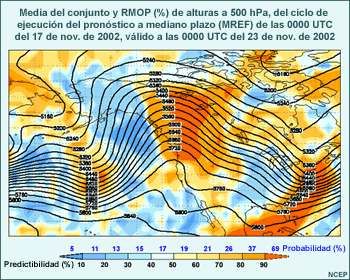
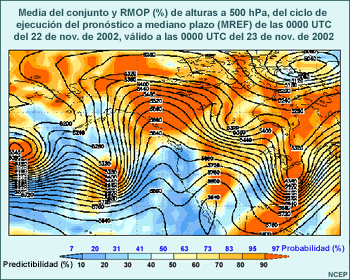
-
Los detalles más difíciles de predecir aparecen suavizados en la media del conjunto. Es probable que la ubicación y la intensidad de las características atmosféricas sea incierta.
-
Puede haber información útil (por ejemplo, más de un pronóstico o agrupamiento probable) en los diagramas espagueti u otros gráficos que muestran los miembros individuales del conjunto. El ejemplo siguiente muestra la predicción por conjuntos de las 12 UTC del 8 de abril de 2002 para la isohipsa de 500 hPa de 564 dm. El pronóstico es válido para las 12 UTC del 16 de abril de 2002.
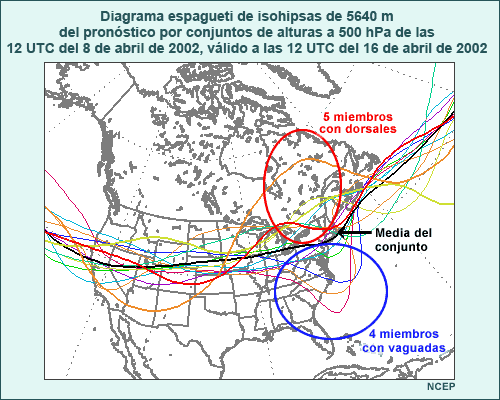
Observe cómo la línea negra, que representa la media del conjunto, es esencialmente zonal, mientras que muchos de los miembros del conjunto muestran dorsales o vaguadas (resaltadas con los círculos) en el este y oeste de los EE. UU.
La escala de las características en los pronósticos para períodos más cortos (12 horas a 3 días) también varía con la predictibilidad del régimen. Las siguientes reglas generales se aplican aquí:
- Los sistemas de predicción por conjuntos a corto plazo (Short Range Ensemble
Forecast, o SREF) de alta resolución se deben usar siempre que estén disponibles en
lugar de los de baja resolución. Por ejemplo, de 0 a 63 horas, las predicciones por
conjuntos de mediano plazo (Medium Range Ensemble Forecast, o MREF) y el SREF están disponibles
en el sitio del NCEP.
- Para plazos de tiempo más cortos, en los sistemas MREF y SREF, las
características de escala más pequeña aparecerán en los pronósticos de la media del
conjunto, porque las diferencias entre los miembros del conjunto no habrán aumentado tanto.
Por consiguiente, la media del conjunto no estará tan suavizada. Por ejemplo, compare los
mapas anteriores de pronósticos de 144 horas y de 24 horas.
- Las reglas para la interpretación de la media y la dispersión de estas
características son las mismas que para las características de gran escala en los
pronósticos de mediano plazo.
- Los SREF pueden centrarse más en la incertidumbre de los detalles del pronóstico, debido a que son de mayor resolución.
- Las reglas para la interpretación de la media y la dispersión de estas
características son las mismas que para las características de gran escala en los
pronósticos de mediano plazo.
Consideraciones adicionales
La predicción por conjuntos presupone el uso de un modelo de PNT «perfecto», con perturbaciones iniciales que toman en cuenta adecuadamente las incertidumbres en las condiciones iniciales. Sin embargo.
Realidad: El modelo de PNT no es perfecto.
- Los pronósticos por conjuntos están sujetos a las mismas asimetrías y errores que el modelo de PNT utilizado para crear los miembros individuales del conjunto. Sin embargo, los pronósticos calibrados consideran la actuación del conjunto durante un período anterior (normalmente 30 días) y se ajustan tomando en cuenta estas asimetrías y errores sistemáticos del modelo. Se deben usar pronósticos calibrados siempre que estén disponibles, teniendo presente el período de tiempo usado para desarrollar la calibración y el carácter del flujo durante ese período.
- Si no hay pronósticos calibrados disponibles, se deben considerar los sesgos y los errores conocidos del modelo de PNT y hacer los ajustes apropiados.
Realidad: La incertidumbre en las condiciones iniciales no se toma siempre en cuenta adecuadamente en los sistemas de predicción por conjuntos.
- Como con los pronósticos deterministas, es importante evaluar las condiciones iniciales. Debemos determinar si la incertidumbre en los miembros del conjunto responde adecuadamente a la incertidumbre en las condiciones iniciales indicada por las observaciones (es decir, satélites, radiosondeos, sistemas ACARS, datos de superficie, etc.).
- Consulte la sección de casos de estudio de esta lección, donde se presenta un ejemplo que ocasionó problemas en la predicción de un evento de nieve que ocurrió en enero de 2002 en el noreste de los EE. UU.
Realidad: los datos del conjunto tienen una resolución horizontal y vertical más baja que los datos de los pronósticos operativos de los mismos modelos.
- Esto es particularmente importante al usar los mapas horizontales de las variables pronosticadas que varían a nivel de mesoescala, como la precipitación, y cualquiera de los productos del conjunto que abarca una celda o columna de malla.
- La interpretación de los datos del conjunto tiene que considerar los efectos de la resolución relativamente baja sobre las predicciones por conjuntos.
Realidad: los datos de la media del conjunto promedian las características inciertas en miembros individuales del conjunto.
- Por lo general, la amplitud de las características de la media del conjunto es menor que la de los miembros individuales.
- Las características de la media del conjunto cuya ubicación no es incierta pero cuyos miembros tienen una amplitud similar aparecen como menos significativas de lo que son en la realidad.
- La dispersión del conjunto se puede utilizar para interpretar la media del conjunto en términos de la distribución de los miembros individuales del conjunto.
Entre otras cosas, una buena interpretación de las predicciones por conjuntos exige considerar la posición de las regiones de alta dispersión en relación con las características de la media del conjunto. Primero estudiaremos algunos patrones idealizados de media y dispersión y diagramas espagueti y después un caso real. Recuerde que los diagramas espagueti y de media y dispersión reales rara vez son tan claros como en las situaciones idealizadas que se describen en los primeros dos ejercicios.
Ejercicios
Interpretación del nivel de 500 hPa con diagrama de media y dispersión del conjunto y diagrama espagueti
Pregunta

Considerando este diagrama idealizado de la media y dispersión, ¿cuál sería la mejor
interpretación de la vaguada en la media del conjunto?
Elija la
mejor respuesta.
La respuesta correcta es b)
La mejor respuesta es (b). La incertidumbre en la amplitud de una característica de la media del conjunto muestra una gran dispersión dentro de esa característica. El diagrama espagueti correspondiente podría ser similar a este gráfico:

Predictibilidad de los regímenes de flujo atmosférico
Pregunta
En la actualidad las oficinas de pronóstico exigen la capacidad de hacer previsiones de hasta 7 días. Con esto en mente, considere este mapa de la medida relativa de predictibilidad que muestra el pronóstico de la media del conjunto y la medida relativa de predictibilidad de las alturas a 500 hPa para un período de 144 horas, realizado a las 0000 UTC del 17 de noviembre de 2002, válido para las 0000 UTC del 23 de noviembre de 2002, durante un evento El Niño, o evento cálido, moderado en el Pacífico ecuatorial central. Los eventos El Niño suelen estar asociados con la formación de una dorsal en el noroeste de Norteamérica y una vaguada en el sudeste de los EE. UU.
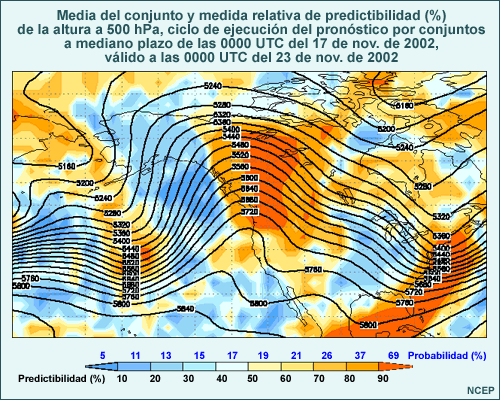
¿Qué puede decir sobre el pronóstico de la media del conjunto de una dorsal en el nivel de 500 hPa en el noroeste de Norteamérica? Elija todas las opciones pertinentes. En las opciones siguientes, el término "verificación" implica que el análisis de verificación del NCEP cae dentro de la misma clase climatológica de 10 % que el pronóstico de la media del conjunto.
Las respuestas correctas son a), c) y d).
Recuerde que la medida relativa de predictibilidad supone que cuanto más miembros coincidan con el pronóstico de la media del conjunto, tanto más predictible será el régimen de flujo. El sombreado representa la medida relativa de predictibilidad para cada punto de la malla de la predicción por conjuntos actual, basado en la media ponderada de la frecuencia con que los miembros del conjunto ocupan la misma clase climatológica que el pronóstico de la media del conjunto en el período de 30 días anterior. El color anaranjado intenso indica una predictibilidad del 90 %, que encontramos en la característica de interés. Por consiguiente, la respuesta a) es correcta.
Sin embargo, una predictibilidad del 90 % no significa que hay una probabilidad de verificación del 90 %. En el mismo período de 30 días, cuando el pronóstico tenía una predictibilidad del 90 %, solo se verificó el 69 % de las veces. Por lo tanto, la respuesta b) es incorrecta, pero c) es correcta.
Finalmente, los eventos El Niño moderados tienden a favorecer la fase positiva del patrón de variabilidad del Pacífico-Norteamérica, o PNA. Durante una fase PNA positiva, son características las alturas por encima de lo normal en el noroeste de Norteamérica y por debajo de lo normal en el sudeste. Como esto significa que la existencia de un evento cálido aumenta nuestra confianza en el pronóstico de alturas de 144 horas, la respuesta d) es correcta también.
Límites de los conjuntos de mediano plazo
Ahora considere la medida relativa de predictibilidad de la media del conjunto para el nivel de 500 hPa del ciclo de ejecución del conjunto de las 0000 UTC del 22 de noviembre de 2002, también válido para las 0000 UTC del 23 de noviembre de 2002, que se muestra a continuación. Compare el pronóstico de 144 horas del ejercicio anterior, válido para el mismo período. También será útil ver los pronósticos de 144 horas para las alturas de 500 hPa de los miembros individuales para ver la posición y la amplitud de las características pronosticadas por cada miembro del conjunto (el enlace permite abrir ventanas adicionales para comparar más fácilmente los mapas).
Pregunta
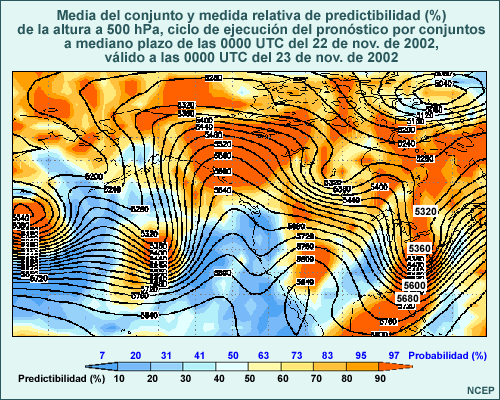
Por ahora, considere el pronóstico de 24 horas de la media del conjunto como una «verificación». Si compara los dos pronósticos verificados a las 0000 UTC del 23 de noviembre de 2002, ¿cuál de las declaraciones siguientes son ciertas? Elija todas las opciones pertinentes.
Las respuestas correctas son a) y d).
No cabe duda de que las características del pronóstico de 144 horas con un alto grado de predictibilidad aparecen cerca de las posiciones pronosticadas. Esto se debe a que las predicciones por conjuntos de mediano plazo suelen ser buenos para predecir la posición de las características de gran escala, o de onda larga, que son más predictibles. Esto significa que la respuesta a) es correcta. Cabe observar, sin embargo, que hay casos individuales en los que las características de pequeña escala pueden también ser bien pronosticadas.
Sin embargo, la amplitud de las características de gran escala, o de onda larga, dependerá del momento y la amplitud de las características de pequeña escala, o de «onda corta», que se mueven a través de las posiciones de las vaguadas y dorsales de gran escala u onda larga. Observamos antes que la amplitud de la dorsal occidental se capturó bien, pero se subestimó el pronóstico de la amplitud de la vaguada oriental en la media del conjunto en unos 100 a 120 metros. La respuesta b) es incorrecta.
El mapa anterior indica que el grado de predictibilidad de la posición del eje de la vaguada en la región central de Canadá varía del 60 al 90 %. En 144 horas, sin embargo, la predictibilidad del eje de la vaguada (que es mucho más débil en la media del conjunto) es solo del 30 al 70 %. Por consiguiente, la respuesta c) es incorrecta.
Un examen de los pronósticos de 144 horas de los miembros individuales para las alturas de 500 hPa permite ver las diferentes posiciones y amplitudes de la vaguada de onda corta. (La misma información se puede también obtener de un diagrama espagueti de las isohipsas críticas.) Si los comparamos con la medida relativa de predictibilidad de la media del conjunto a las 144 horas, vemos que las diferencias entre los pronósticos de los miembros del conjunto de 144 horas se suavizaron al promediar los pronósticos de los miembros del conjunto (para llegar a la media del conjunto), debilitando así las características. Esto significa que la respuesta d) es correcta. Observe que las vaguadas de onda corta en el Pacífico Este, al oeste de los EE. UU., y la región central de Canadá se pueden encontrar en los miembros individuales del conjunto del pronóstico de 144 horas, pero en posiciones distintas y con amplitudes diferentes. Observe que la existencia coherente de una característica de pequeña escala puede brindar información útil, incluso si su posición y/o amplitud no se pronostican de forma coherente.
Verificación
Introducción
Todos los pronósticos numéricos se deben verificar para comprobar y mejorar su utilidad. Para los pronósticos individuales, suelen utilizarse herramientas estadísticas simples de sesgo (frío o cálido, húmedo o seco, alto o bajo, etc.) y de error cuadrático medio (como medida de la «distancia» entre el pronóstico y la verificación). Estas herramientas se pueden aplicar a un único punto o a varios puntos de un área de interés. Para las predicciones por conjuntos, también se pueden aplicar estas y otras herramientas estadísticas típicas al valor medio de una variable meteorológica o al valor de un miembro individual.
Con la predicción por conjuntos, sin embargo, no deseamos evaluar solo la exactitud del pronóstico de un miembro individual o de la media del conjunto. Como el propósito final de la predicción por conjuntos es obtener un cuadro exacto de la distribución de probabilidad de los eventos posibles, es importante verificar esa distribución y sus cualidades estadísticas. Esto incluye, entre otras cosas:
- determinar la verificación dentro del rango de pronósticos ofrecidos por varios miembros del conjunto;
- determinar cómo las probabilidades de los eventos pronosticados por conjuntos «coinciden» con la frecuencia con la que se observan los eventos; y
- determinar la utilidad de la predicción por conjuntos en relación con la climatología y los pronósticos y deterministas.
El propósito de esta sección es ayudar a las y los pronosticadores operativos a entender los aspectos clave de la verificación de las predicciones por conjuntos de modo que puedan:
- interpretar mejor los productos de verificación del conjunto; y
- mejorar el uso de los sistemas de predicción por conjuntos en el proceso de pronóstico.
Conceptos
Dos tipos de productos de predicción por conjuntos
Los pronósticos categóricos declaran «categóricamente» que un conjunto de eventos tendrá lugar o no. Como estos pronósticos son «binarios» por naturaleza, siendo «sí» y «no» las únicas posibilidades, la probabilidad de un evento es del 0 o del 100 %. Un ejemplo de múltiples categorías sería un conjunto de temperaturas enteras de 30 a 38 °C. Los pronósticos categóricos con solo dos resultados posibles se denominan dicotómicos; un ejemplo sería decir que la temperatura de hoy será igual o mayor que 32 °C. La verificación de un pronóstico categórico implica usar conceptos tales como «índices de aciertos» e «índices de falsas alarmas», que se explican en la sección 5.1.2.
Los pronósticos probabilísticos describen la probabilidad de que se produzcan uno o varios eventos meteorológicos y, por lo tanto, expresan el grado de incertidumbre. La variable pronosticada puede adquirir valores discretos o continuos. Las variables continuas deben, sin embargo, volverse a organizar en valores o subrangos discretos (por ejemplo, las temperaturas enteras de 30 a 38 °C) para poder calcular las probabilidades. Las probabilidades de los eventos están siempre dentro del rango que va del 0 al 100 %.
La primera gráfica muestra un pronóstico probabilístico hipotético de la temperatura máxima. La segunda describe los mismos datos del pronóstico con solo dos rangos: temperaturas por debajo de 32 °C y temperaturas iguales o mayores que 32 °C (observe que en la escala vertical el intervalo en la primera gráfica es del 5 %, mientras que en la segunda es del 20 %).

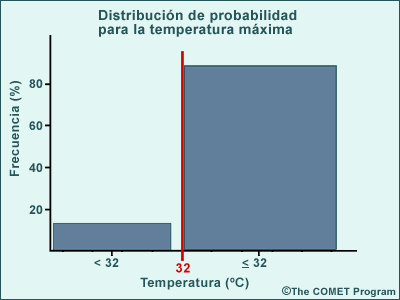
Los incrementos usados para resolver la distribución de la probabilidad (es decir, el tamaño de las «clases» o categorías del eje horizontal) son arbitrarios y se pueden fijar para satisfacer las necesidades del momento. La verificación de las distribuciones de probabilidad se realiza comparando las probabilidades del pronóstico con las frecuencias de verificación y se basa en los conceptos de confiabilidad y resolución.
Verificación de los pronósticos categóricos de un SPC
Los términos «acierto» y «falsa alarma» se utilizan para los pronósticos categóricos (sí/no). Se produce un acierto cuando o la ocurrencia o la no ocurrencia del evento se pronostica correctamente (las celdas «sí/sí» y «no/no» de una tabla de contingencia). Por otra parte, se da una falsa alarma cuando se pronostica un evento, pero no se observa (celdas «sí/no»). El índice de aciertos se define como:
- la razón entre todos los pronósticos correctos («sí/sí» y «no/no») y todas las observaciones
mientras que la definición típica de índice de falsas alarmas es la razón entre las
falsas alarmas (pronósticos «sí» con verificación «no») y el número de
veces que un evento fue pronosticado. (NOTA: encontrará una descripción de una
segunda definición usada en el diagrama de características operativas relativas (Relative
Operating Characteristics, o ROC), en la sección «Herramientas de
verificación».) Tanto los aciertos como las falsas alarmas se pueden mostrar por medio de
una tabla de contingencia que compara los eventos pronosticados y los eventos observados, como
esta:
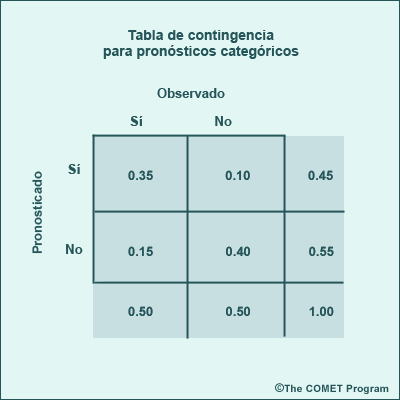
Obviamente, un buen pronóstico tendrá un índice de aciertos mayor que el índice de falsas alarmas. El índice de aciertos para los datos anteriores es (35+40)/100 («sí/sí» más «no/no» dividido entre la cantidad de observaciones), es decir 0,75. El índice de falsas alarmas es 10/(35+10) = 0,22 (la celda «sí/no» dividida entre la cantidad total de veces que se pronosticó el evento, es decir, las celdas «sí/sí» + «sí/no»).
La relación entre el índice de aciertos y el índice de falsas alarmas sobre un rango completo de probabilidades se muestra en el diagrama de características operativas relativas (Relative Operating Characteristics, o ROC) que se describe más adelante, en la sección sobre Herramientas de verificación.
El concepto de habilidad
La habilidad es una medida de la precisión que requiere una comparación; es decir, habilidad relativa ¿a qué? Generalmente, la habilidad de un pronóstico se calcula comparándolo con un pronóstico de habilidad cero, como la climatología o la persistencia (por ejemplo, el pronóstico de hoy es el mismo que la verificación de ayer). Esto no quiere decir que los pronósticos de habilidad cero sean necesariamente malos, desde luego, sino que no requieren ninguna habilidad para producirlos y, por tanto, no ofrecen ningún valor agregado, que es lo que estamos intentando medir. El índice de habilidad se obtiene comparando alguna medida objetiva de la precisión del pronóstico (como el índice de aciertos) con la precisión de ese patrón de referencia. En términos generales, el índice de habilidad se calcula de la siguiente manera:
donde la «precisión perfecta» (siempre 1,00 o el 100 %) indica que la verificación es siempre correcta. Cualquier índice de habilidad positivo (numerador mayor que cero) indica una mayor habilidad del pronóstico con respecto a la habilidad de referencia. Los índices de valor cero o negativos indican una habilidad nula. Por ejemplo, si a lo largo de un período fijo un pronóstico se verifica el 60 % de las veces y la climatología se verifica el 30 % de las veces, la habilidad para ese período sería:
es decir, el 42,8 %
Los índices de habilidad se utilizan para medir la confiabilidad y la resolución de los pronósticos categóricos o probabilísticos. En la próxima sección describiremos las herramientas específicas empleadas para evaluar la resolución y la confiabilidad de las predicciones por conjuntos.
Verificación de los pronósticos categóricos de un SPC
Para verificar el SPC es necesario comparar pronósticos probabilísticos por conjuntos con la frecuencia de las observaciones a lo largo del tiempo. Una buena verificación requiere un gran número de pronósticos por conjuntos para obtener resultados estables.
Confiabilidad y resolución
Utilizamos dos medidas estadísticas para evaluar la medida en que coinciden los pronósticos y las observaciones. Se deben considerar ambas para lograr la mejor evaluación posible de un SPC.
- La confiabilidad mide el grado en que la distribución de probabilidad de
las predicciones por conjuntos coincide con la distribución de verificación. Supongamos, por
ejemplo, que deseamos saber cuánto podemos confiar en un conjunto cuando pronostica un
40 % de probabilidad de precipitación. Si examinamos cómo todos las predicciones por
conjuntos con un 40 % de probabilidad de precipitación se verificaron en el pasado,
podemos obtener una medida de la confiabilidad del este conjunto. La evaluación de la
confiabilidad también se conoce como calibración, porque los resultados se pueden utilizar
para «calibrar» una distribución de pronósticos por conjuntos para eliminar del
SPC sesgos y errores de pronóstico sistemáticos.
Si las probabilidades del pronóstico y las frecuencias de verificación subsecuentes coinciden exactamente, el SPC es absolutamente confiable. Por otra parte, si la frecuencia de verificación es más alta o más baja que el pronóstico, este se consideraría, respectivamente, subestimado o exagerado. En el diagrama siguiente, el pronóstico ha subestimado los valores extremos de la variable de interés y también se nota un sesgo hacia valores bajos; en consecuencia, la distribución del pronóstico es más angosta y está desplazada hacia la izquierda frente a la distribución de verificación.
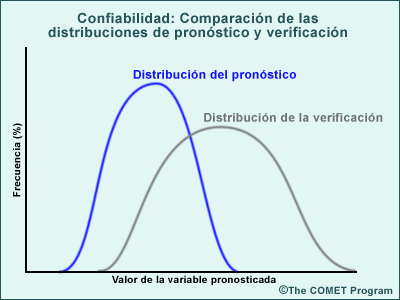
- La resolución cuantifica la respuesta a la pregunta ¿coinciden
las distribuciones de probabilidad de pronósticos diferentes del SPC con las
distribuciones de probabilidad de verificación igualmente diferentes? Por ejemplo,
considere las gráficas que aparecen a continuación, en las cuales se muestran distribuciones
hipotéticas de pronósticos por conjuntos (azul indica frío, rojo indica cálido), la
distribución de verificación de alguna variable (digamos la temperatura a 2 m) y la
distribución climatológica de la variable (curva de trazos verde).
En términos generales, si la distribución de probabilidad de las predicciones por conjuntos difiere de la distribución climatológica utilizada en la verificación de manera similar a como la distribución de probabilidad de las observaciones difiere de la distribución climatológica (en verde), se considera que el SPC es de alta resolución. La figura siguiente muestra un ejemplo de un SPC de alta resolución. En la gráfica de la izquierda, el pronóstico de temperatura a 2 m más frío de lo normal (el pronóstico A, en azul) coincide bien con la fuerte tendencia observada hacia temperaturas más frías que lo normal (en azul, gráfica de la derecha). Lo mismo puede decirse para el pronóstico B en rojo.
(Nota: la confiabilidad no es perfecta porque el pronóstico ha subestimado los extremos de las distribuciones OBSERV. A y OBSERV. B.)
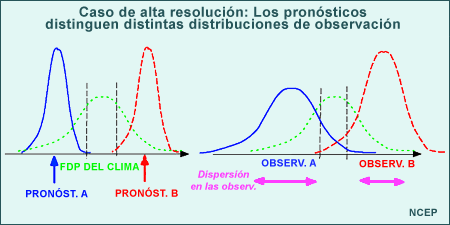
Sin embargo, cuando las distribuciones de las predicciones por conjuntos de carácter muy diferente están asociadas con verificaciones similares entre sí, se considera que su resolución es baja. Esto se muestra conceptualmente en la figura siguiente. Los pronósticos frío y cálido (A y B, respectivamente) están asociados con observaciones que se asemejan entre sí y a la climatología.
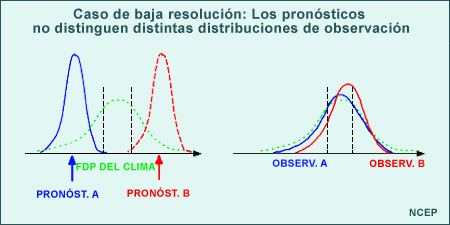
Ajustes para mejorar la confiabilidad y la resolución
Una confiabilidad baja se puede aumentar ajustando la distribución del pronóstico utilizando la relación pasada conocida entre las distribuciones de pronóstico y de las observaciones (suponiendo que no se producen cambios significativo en esa relación). Consideraremos la «calibración» del pronóstico en el apartado «Productos» de la sección «Resumen de los datos». Sin embargo, la calibración no podrá mejorar un pronóstico sin buena resolución, de forma que se deben tener en cuenta tanto la resolución como la confiabilidad para proceder a una evaluación completa del SPC.
Los pronósticos con resolución baja no se pueden mejorar estadísticamente. Por ejemplo, si calibráramos las predicciones por conjuntos de la figura anterior para corregir sus sesgos cálido y frío aparentes, en el futuro obtendríamos siempre distribuciones que se ajustan a la climatología, por lo que no valdría siquiera la pena tomarse la molestia de ejecutar el SPC. Dadas situaciones como la anterior, la única manera de mejorar el pronóstico consiste en mejorar el modelo del SPC de modo que los pronósticos que genere puedan distinguir, por ejemplo, verificaciones cálidas y frías, o húmedas y secas.
Herramientas
Herramientas estadísticas
Existen herramientas estadísticas diseñadas para datos probabilísticos que permiten evaluar la confiabilidad y/o la resolución de las distribuciones de probabilidad de los pronósticos del SPC. ¿Qué importancia tiene la verificación? Es importante saber, por ejemplo:
- si el pronóstico de un SPC exagera o subestima las probabilidades;
- cuán probable es que el SPC capture todos los resultados posibles del pronóstico;
- si el SPC tiene sesgos o no; etc., etc., etc.
La tabla siguiente enumera algunas de estas herramientas en función de las características que permiten evaluar. Entre paréntesis se indica la subsección en la cual se explica cada una ellas.
|
Característica de distribución de probabilidad a evaluar
|
Herramientas de evaluación empleadas
|
|---|---|
|
Confiabilidad y resolución
|
Índice de Brier (Brier Score, o BS)
Índice de habilidad de Brier (Brier Skill Score, o BSS) Diagramas de confiabilidad/atributos Índice de habilidad de probabilidades clasificadas (Ranked Probability Skill Score, o RPSS) |
|
Confiabilidad
|
Diagrama de Talagrand (histograma de análisis de rangos)
|
|
Resolución
|
Características operativas relativas (ROC) |
Índice de Brier (BS) e índice de habilidad de Brier (BSS)
Los conceptos de confiabilidad y resolución se resumen sucintamente en una estadística conocida como índice de Brier (Brier Score, o BS). El índice de Brier empareja pronósticos categóricos y observaciones. Para cada evento pronosticado, se asigna un valor de 1 a los pronósticos y las verificaciones que caen en una categoría particular y un valor de 0 a los que caen en otras categorías. Los valores de las parejas de pronósticos y observaciones se restan y se elevan al cuadrado (dando por resultado 0 o 1), se suman y luego se dividen por el número de parejas, lo cual da como resultado un valor entre 0 y 1. Cuanto más próximo a cero sea el valor de índice de Brier, tanto mejor es el pronóstico.
El índice de habilidad de Brier (Brier Skill Score, o BSS) compara el índice de Brier de un pronóstico con el de una referencia, normalmente la climatología. Este valor oscila entre uno (mejor) y cero (peor), al contrario del índice de Brier.
Para ver algunos ejemplos de BS y BSS, vamos a considerar los datos hipotéticos de la tabla siguiente que corresponden a la predicción por conjuntos de la temperatura media al día 2 y las verificaciones subsecuentes para 30 días de calendario consecutivos. Utilizamos la climatología de largo plazo del lugar para clasificar las temperaturas en clases iguales del 33 % por debajo de lo normal, normal y por encima de lo normal. El orden dado es pronóstico/verificación. Los días en los que solo hubo errores de pronóstico se muestran en rojo. Los días en los que el pronóstico se verificó, pero la climatología no (mayor o menor que lo normal) se muestran en azul. Los días en los que ni el pronóstico ni la climatología se verificaron aparecen en violeta.
| Debajo de lo normal |
1/1 |
1/0 |
0/0 |
0/0 |
0/0 |
1/0 |
0/0 |
0/0 |
1/1 |
1/1 |
0/0 |
0/0 |
0/0 |
0/1 |
0/0 |
| Próximo a lo normal |
0/0 |
0/1 |
0/0 |
1/1 |
1/1 |
0/0 |
1/1 |
1/1 |
0/0 |
0/0 |
1/1 |
1/1 |
1/1 |
0/0 |
0/0 |
| Encima de lo normal |
0/0 |
0/0 |
1/1 |
0/0 |
0/0 |
0/1 |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
1/0 |
1/1 |
| Debajo de lo normal |
0/0 |
0/0 |
1/1 |
1/1 |
1/0 |
0/0 |
0/0 |
0/0 |
0/0 |
1/1 |
1/1 |
1/1 |
0/0 |
0/0 |
0/0 |
| Próximo a lo normal |
1/1 |
1/1 |
0/0 |
0/0 |
0/1 |
1/1 |
1/1 |
1/1 |
1/1 |
0/0 |
0/0 |
0/0 |
1/1 |
1/1 |
1/1 |
| Encima de lo normal |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
0/0 |
Para este caso en que pronosticamos estas categorías de temperatura, (con tres días de 30 errados), el índice de Brier se calcula de la forma siguiente:
BS = 3 x (1/30) = 0,1
El pronóstico climatológico (próximo a la normal) para cada día en este período produce un índice de Brier de 12 x 1/30 (es decir, 12 días con errores de 30) o 0,4. Si utilizamos la climatología como medida de referencia para el índice de habilidad de Brier, la fórmula de índice de habilidad nos permite calcular el siguiente resultado:
BSS = (0,1 – 0,4) ÷ (0 – 0,4) = 0,75
Ejemplo de productos del índice de Brier
El uso del índice de Brier en el Servicio Nacional de Meteorología de EE. UU. puede verse en la figura siguiente, obtenida del sitio del Centro de Predicción Hidrometeorológica (Hydrometeorological Prediction Center, o WPC). El diagrama muestra el valor de probabilidad de precipitación (POP) de los días 3 a 7 para los pronósticos de precipitación del WPC generados por humanos para el período de julio de 2003 a julio de 2004. Observe que el índice de Brier aumenta (indicando menos habilidad) a medida que aumenta el plazo de pronóstico y es mayor en verano que en invierno.
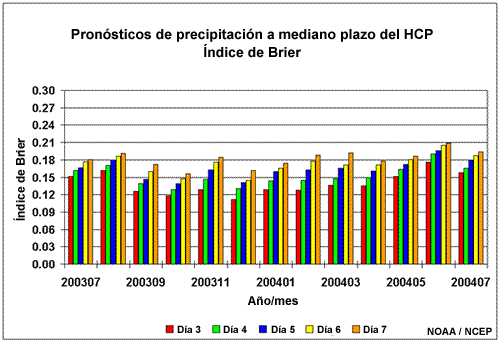
A fondo: ceonfiabilidad, resolución y BS/BSS
Componentes del índice de Brier (BS) y del índice de habilidad de Brier (BSS)
Con un poco de álgebra, el índice de Brier se puede dividir en tres componentes (véase, por ejemplo, Wilks 1995, 261-263):
BS = confiabilidad - resolución + incertidumbre
La contribución de cada término al BS es la siguiente:
- La confiabilidad depende del cuadrado de las diferencias entre las probabilidades del
pronóstico y de verificación, de modo que cuanto más pequeño el índice de Brier, mejor.
- La resolución depende del cuadrado de las diferencias entre las probabilidades de
verificación y la probabilidad climatológica, de modo que cuanto más grande el índice de
Brier, mejor.
- El término de incertidumbre depende de la variabilidad de las observaciones y, por tanto,
está fuera del control de la pronosticadora.
- Cuanto más cercana la probabilidad climatológica de los valores extremos (ocurre
siempre o no ocurre nunca), más baja será la variabilidad y la contribución al
índice de Brier se reduce al mínimo.
- Si la probabilidad de que se produzca un evento es igual a la probabilidad de que no se produzca (probabilidad climatológica de 0,5), la variabilidad de las observaciones y la contribución de la incertidumbre al índice de Brier se maximiza.
- Cuanto más cercana la probabilidad climatológica de los valores extremos (ocurre
siempre o no ocurre nunca), más baja será la variabilidad y la contribución al
índice de Brier se reduce al mínimo.
Puesto que un valor de índice de Brier perfecto es cero, el índice de habilidad de Brier se puede escribir así:
BSS = (BSpronóst - BSclima) / (0 - BSclima) = 1 - (BSpronóst / BSclima)
Determinación del área de habilidad cero en el diagrama de confiabilidad
Puede demostrarse que BSclima representa la incertidumbre y, por tanto, es equivalente a:
BSS = (resolución - confiabilidad) / incertidumbre
La fórmula nos permite ver que:
- siempre que la resolución sea mayor que la confiabilidad, la habilidad de pronóstico será positiva; y
- la línea que indica que la resolución y la confiabilidad son iguales marca el límite superior de la zona de habilidad cero en el diagrama de confiabilidad.
En otras palabras, cuando la confiabilidad es menor o igual que la resolución, la habilidad del pronóstico es cero. Este resultado nos permite trazar la línea de «habilidad cero» en un diagrama de confiabilidad/atributos (vea la sección 5.2.3).
Diagrama de confiabilidad/de atributos
Podemos visualizar la resolución y la confiabilidad de un SPC trazando la frecuencia de las probabilidades pronosticadas frente a la frecuencia de verificación asociada. El resultado es un diagrama de confiabilidad (o de atributos) que compara el resultado con:
- Un pronóstico del SPC perfectamente confiable en el cual las probabilidades del pronóstico y de la verificación coinciden perfectamente (la línea diagonal azul del diagrama).
- Una línea de «habilidad cero», que se puede derivar del índice de habilidad de Brier, trazada a través de puntos equidistantes de la línea de confiabilidad perfecta y la línea de climatología (resolución cero). NOTA: encontrará más detalles en la sección A fondo .
- Dos líneas adicionales que representan el pronóstico de la probabilidad climatológica en todos los momentos (línea vertical color magenta) y la ocurrencia de la probabilidad climatológica para todas las probabilidades de pronóstico (línea horizontal color magenta).
- Se suele incluir un panel adicional que indica el número de veces que cualquier categoría climatológica fue pronosticada en cada uno de los posibles niveles de probabilidad.
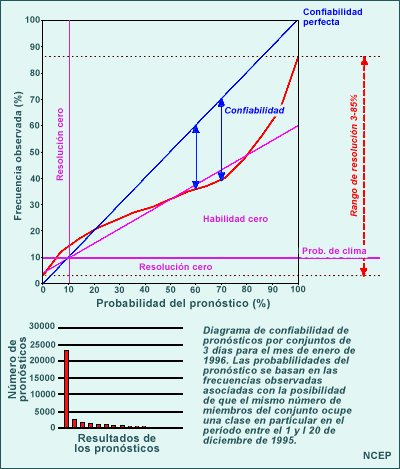
Para crear el diagrama de confiabilidad anterior, se clasificaron los datos de alturas de 500 hPa de cada ciclo de ejecución de la predicción por conjuntos para un período de 20 días, en 10 clases climáticas igualmente probables (las mismas clases utilizadas para el ejemplo del producto de medida relativa de predictibilidad del conjunto usado en la sección anterior). Para cada ciclo de ejecución, el porcentaje de los miembros del conjunto que están de acuerdo (es decir, que caen en la misma clase) representa la probabilidad del pronóstico de que se produzca ese resultado. En el diagrama anterior, la posición del 0 % representa aquellos casos en que ningún pronóstico cae en una categoría, mientras la posición del 100 % indica que todos los pronósticos caen en la misma clase. El diagrama muestra cómo se comparan estas probabilidades con la frecuencia con que las observaciones subsecuentes caen en la misma clase.
- La línea roja en el diagrama de probabilidad marca la frecuencia de ocurrencia observada para una probabilidad dada del pronóstico. Por ejemplo, para una probabilidad de la predicción por conjuntos del 70 %, hay una probabilidad del 40 % de que el pronóstico se verifique; en otras palabras, cuando 7 miembros de un conjunto de 10 miembros pronostican valores que caen en la misma clase, un valor de ese rango se verificará el 40 % de las veces. La punta inferior de la flecha azul vertical de la derecha en el diagrama anterior representa ese punto en la curva de confiabilidad. El hecho de que parte de la curva cae debajo de la línea de confiabilidad perfecta indica que el conjunto exagera el pronóstico con probabilidades arriba del 20 %, pero subestima ligeramente el pronóstico con probabilidades por debajo del 20 %
- La probabilidad de verificación de la climatología es del 10 %, en virtud de las clases climatológicas elegidas, tal como lo indican las líneas vertical y horizontal color magenta en el diagrama.
- El gráfico de columnas de la izquierda inferior muestra el número de pronósticos para cada nivel de probabilidad. La mayor parte cae en el rango de probabilidad del 0 % (la columna roja más alta, a la izquierda) porque para cada predicción por conjuntos varias clases climatológicas pueden estar subrepresentadas por algunos de los miembros del conjunto. Muy pocos pronósticos caen en los niveles de probabilidad más altos, porque es relativamente raro que el 80, el 90 o el 100 % de los miembros del conjunto coincidan en una sola clase.
- El rango de frecuencias observadas para todas las probabilidades pronosticadas (entre cero y el 100 %) es el rango de resolución de los conjuntos. En este caso, el rango de resolución va del 3 al 85 %. Esencialmente, esto representa los puntos finales de la distribución de probabilidad con respecto a la distribución de verificación, y la pendiente de la línea roja muestra variaciones de resolución en el rango completo de probabilidades pronosticadas. Observe que el 3 % de las veces que la predicción por conjuntos indicaba que el evento no ocurriría (es decir, ningún pronóstico cayó en esa clase), el evento sí ocurrió, y que el 14 % de las veces que el pronóstico indicó una probabilidad del 100 % de que ocurriera el evento (es decir, que todos los miembros del conjunto caerían en la misma clase), el evento no ocurrió. Esto implica que el sistema de predicción por conjuntos subestima las probabilidades bajas y exagera las probabilidades altas, aunque en total parece resolver razonablemente bien las situaciones con verificaciones de baja y alta probabilidad. Cuanto más recta sea la línea roja para un rango de probabilidades, tanto peor será la resolución del pronóstico en ese rango. Por consiguiente, el sistema de predicción por conjuntos de este ejemplo es bueno para resolver la probabilidad en los extremos, pero no tan bueno en los rangos medios.
- La distancia entre la línea roja y la línea azul da la medida de confiabilidad (cero es perfecto). Observe que, en general, cuanto más mayor la muestra de datos, tanto más representativa será de la confiabilidad del comportamiento del SPC a largo plazo.
Características operativas relativas (ROC)
Las características operativas relativas (Relative Operating Characteristics, o ROC) determinan la calidad de los pronósticos categóricos comparando los índices de aciertos y de falsas alarmas (o probabilidad de detección falsa) para los eventos o umbrales pronosticados. Cuando se trazan los resultados, se obtiene un diagrama ROC. El diagrama ROC se puede también utilizar para los pronósticos probabilísticos, si se utilizan umbrales de probabilidad para determinar si el pronóstico es un acierto, una falla o una falsa alarma. Por definición, a fin de calcular el diagrama ROC el índice de aciertos y de falsas alarmas puede variar de 0,0 a 1,0 y la curva ROC debe comenzar en el origen (0,0, 0,0) y terminar en (1,0, 1,0).
Para ilustrar el diagrama ROC, utilizamos los datos de 14 miembros del SPC del NCEP con la resolución espectral T62 (una resolución de malla de cerca de 225 kilómetros), para desarrollar los pronósticos de probabilidad de 5 días para las alturas a 500 hPa, entre abril y junio de 1999. Las probabilidades de pronóstico fueron definidas como el porcentaje de miembros del conjunto de cada pronóstico que cae en 10 clases climáticas igualmente probables (las mismas utilizadas en el diagrama de confiabilidad de la sección anterior y la medida relativa de predictibilidad) en cada punto de malla del hemisferio norte. Para los propósitos de medición, se ignoraron los pronósticos con una probabilidad del 0 %. Luego se utilizaron las probabilidades de pronóstico que no son cero (1/14, 2/14, etc., hasta 14/14 o 1,0) como umbrales para determinar los aciertos frente a las falsas alarmas. Aquí, se produce un acierto si la frecuencia de verificación es igual o excede la frecuencia del pronóstico. Inversamente, se produce una falsa alarma si la frecuencia de verificación es menor que la del pronóstico.
A continuación se trazó en el diagrama ROC siguiente cada una de las parejas resultantes de los índices de aciertos y falsas alarmas para generar la curva ROC (en rojo). Una vez trazados los puntos, se dibuja la curva conectando el punto más alto y el punto más bajo a los puntos (1,0, 1,0) y (0,0, 0,0), respectivamente. Se muestran los índices de aciertos y falsas alarmas del pronóstico operativo, para fines de comparación, con una línea de trazos azul. Cuando en un pronóstico los aciertos y las falsas alarmas son equivalentes, se considera que la habilidad del pronóstico es cero. Este umbral de habilidad cero está representado por la línea diagonal negra.
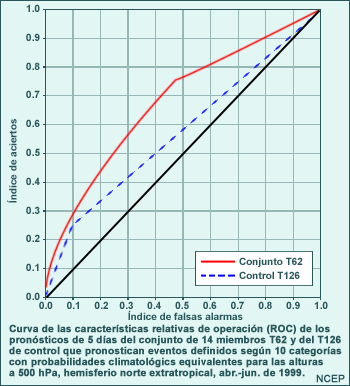
Los valores de característica relativa de operación se determinan midiendo el área debajo de la curva ROC. Se puede utilizar cualquier método razonable para medir esta área (por ejemplo, la regla trapezoidal), siempre que se aplique de forma coherente. Los valores altos se aproximarán a 1,0 (el cuadrado completo) y se consideran bajos aquellos valores que están por debajo de 0,5 (el área debajo de la línea de habilidad cero). En este diagrama, el valor estimado es de 0,68 (usando la regla trapezoidal para medir el área), lo cual indica que los pronósticos categóricos de 5 días para las alturas de 500 hPa tienen cierto grado de habilidad. Observe que para obtener el índice de habilidad algunos centros meteorológicos restan 0,5 (el área bajo la línea de habilidad cero) al área debajo de la curva ROC. Es interesante observar que el pronóstico de 5 días del conjunto de baja resolución tiene una habilidad mayor que el pronóstico operativo a resolución más alta.
Los valores de característica relativa de operación (el área debajo la curva) para diferentes plazos de la predicción por conjuntos se utilizan a menudo para evaluar la duración de la habilidad en los pronósticos. El ejemplo siguiente, proveniente del sitio EMC del NCEP, compara la predicción por conjuntos de mediano plazo del NCEP (rotulado «ROC-ENS»), el conjunto de control (rotulado «ROC-CTL») y el modelo GFS operativo de alta resolución (rotulado «ROC-MRF»). El período cubierto es el mes de febrero de 2004 e incluye valores de característica relativa de operación para los pronósticos de 1 a 15 días (una vez restado 0,5). Observe que el conjunto da el mejor resultado. En comparación el modelos GFS y el conjunto de control quedan muy por debajo.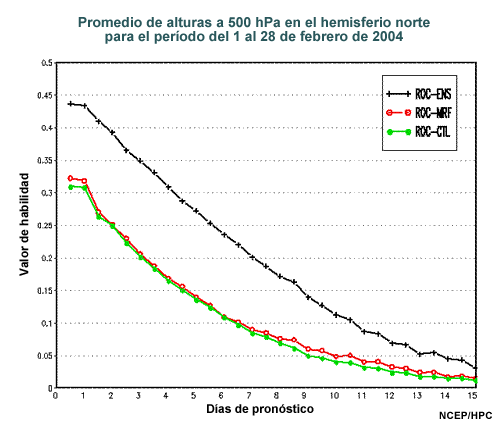
Índice de probabilidades en categorías. Índice de habilidad de probabilidades clasificadas
El índice de probabilidades clasificadas (Ranked Probability Score, o RPS) es análogo al índice de Brier (BS), pero se aplica a múltiples categorías (valores discretos de pronóstico) y es una medida de la «distancia» entre las distribuciones de probabilidad acumulativa del pronóstico y de la verificación. Para calcular el índice de probabilidades clasificadas, clasificamos las categorías y las probabilidades con ellas asociadas del valor más bajo al más alto. Se calculan las diferencias entre las parejas correspondientes a las probabilidades acumulativas de los pronósticos y de la verificación, se elevan al cuadrado y luego se suman. A igual que con el índice de Brier, cero es el resultado perfecto.
Para ver un ejemplo del cálculo, considere el siguiente pronóstico hipotético de la probabilidad de precipitación acumulada en 24 a 36 horas, dividido en tres categorías, el cual se compara la eficiencia de dos pronósticos del SPC en el curso de un mes.
|
Cantidad de precipitación
en 12 h para pronósticos de 24-36 h |
Conjunto 1
|
Conjunto 2
|
Observación
|
|||
|
Probabil.
|
Probabilidad acumulativa
|
Probabil.
|
Probabilidad acumulativa
|
Probabil.
|
Probabilidad acumulativa
|
|
|
< 2 mm
|
0,2
|
0,2
|
0,1
|
0,1
|
0
|
0
|
|
2-13 mm
|
0,6
|
0,8
|
0,6
|
0,7
|
1
|
1
|
|
> 13 mm
|
0,2
|
1,0
|
0,3
|
1,0
|
0
|
1
|
Supongamos ahora que la verificación cayó en el intervalo de 2-13 mm, de forma que esa categoría tiene una probabilidad de 1 en la columna de probabilidad de la observación.
El RPS se calcula elevando al cuadrado las diferencias entre la probabilidad acumulativa del pronóstico y de la observación:
RPS conjunto 1 = (0,2-0,0)2 +(0,8-1)2 +(1-1)2 = 0,08
RPS conjunto 2 = (0,1-0,0)2 +(0,7-1)2 +(1-1)2 = 0,10
Como el conjunto 2 asignó menos peso a la categoría de precipitación menor y más a la categoría mayor, su índice no es tan bueno como el del conjunto 1. Si suponemos que la verificación dio resultados > 13 mm, el resultado cambia a 0,68 para el conjunto 1 y 0,50 para el conjunto 2. El conjunto 2 mejora en este escenario, reflejando el mayor peso asignado a la categoría más alta.
RPS conjunto 1 = (0,2-0,0)2 +(0,8-02 +(1-1)2 = 0,68
RPS conjunto 2 = (0,1-0,0)2 +(0,7-0)2 +(1-1)2 = 0,50
El RPSS incluye una medida de la habilidad
Si tenemos muchas probabilidades y verificaciones del pronóstico, podemos crear un índice de la habilidad de probabilidades clasificadas (Ranked Probability Skill Score, o RPSS) a partir del RPS. Normalmente, la habilidad se mide en relación con la climatología y se toma como la razón del promedio de los valores de RPS del pronóstico y de la climatología para un número dado de pronósticos restada de uno. Los valores van desde uno (mejor) hasta cero (peor).
El diagrama de Talagrand o histograma de análisis de rangos
El diagrama de Talagrand brinda una representación de la confiabilidad de un SPC para períodos de uno a cuatro meses. El Talagrand es un tipo de histograma (gráfico de columnas) en el cual las categorías asociadas a cada columna son rangos variables en lugar de valores discretos, es decir, un histograma de rangos. La forma del diagrama de Talagrand, nos permite sacar conclusiones sobre los sesgos del sistema de predicción por conjuntos y el alcance de su dispersión. Un histograma plano en el cual todas las columnas son iguales indica una confiabilidad perfecta. Otros patrones brindan información sobre los tipos de sesgos y las dispersiones imperfectas (vea el apartado sobre interpretación, más adelante).
Examinemos los componentes de un diagrama de Talagrand.
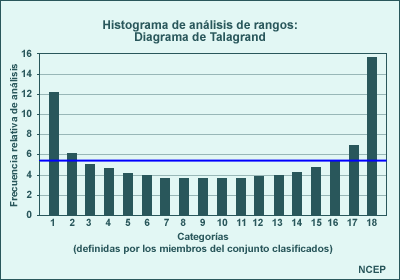
- El eje horizontal representa clases cuyos valores mínimos y máximos están definidos por los
miembros mismos del conjunto, clasificados del valor más bajo al más alto (en otras
palabras, las clases son los rangos entre los miembros de pronósticos por conjuntos). Cada
celda de la malla en cada dominio del pronóstico, tiene un conjunto exclusivo de clases
definidas de esta manera para cada pronóstico. El eje horizontal no contiene el valor de los
rangos, sino que indica simplemente que se utilizaron los mismos rangos de límites de clase
en cada pronóstico del SPC. El valor de los rangos puede variar bastante. Si dos miembros
del conjunto tienen el mismo valor, sus clases se combinan. Por ejemplo, si dos miembros del
conjunto tienen el mismo valor (por decir, 5650 metros) en determinado punto del ciclo de
ejecución del conjunto y fueron clasificados como 9 y 10, después de la clase 8, la clase 9
se combinaría con la clase 10. No habría ninguna contribución a la clase 9 para ese punto y
en ese momento.
- NOTA: la primera clase representa el rango HASTA el miembro del conjunto de la clase
más baja, mientras que la última clase representa el rango por encima del miembro
del conjunto en la clase más alta. Esto significa que hay n+1 clases en el diagrama.
- NOTA: la primera clase representa el rango HASTA el miembro del conjunto de la clase
más baja, mientras que la última clase representa el rango por encima del miembro
del conjunto en la clase más alta. Esto significa que hay n+1 clases en el diagrama.
- Las frecuencias mostradas por las columnas representan el porcentaje de veces que el
análisis del modelo (el término aquí empleado para la verificación) cae en los rangos o las
clases definidas por los miembros de la predicción por conjuntos en cada punto de la malla
del dominio del pronóstico, dentro del período de verificación (en este ejemplo el período
es de 3 meses).
- NOTA: la primera clase contiene las verificaciones que son menores
que el miembro del conjunto en la clase más baja, mientras que la última clase
contiene las verificaciones que son iguales o más altas que el miembro del conjunto
en la clase más alta. Note también que si una observación es igual a uno de los
miembros del conjunto, esta se divide entre las dos clases adyacentes.
- NOTA: la primera clase contiene las verificaciones que son menores
que el miembro del conjunto en la clase más baja, mientras que la última clase
contiene las verificaciones que son iguales o más altas que el miembro del conjunto
en la clase más alta. Note también que si una observación es igual a uno de los
miembros del conjunto, esta se divide entre las dos clases adyacentes.
- La línea azul en el gráfico marca la frecuencia teórica en cada categoría para un SPC perfectamente confiable. Esta frecuencia es 1/(n+1), donde n es el número miembros del conjunto del SPC. Esto supone que si el SPC está bien construido, en una muestra grande cada miembro tiene la misma probabilidad de verificarse, es decir, que el esquema de generación crea un rango de miembros igualmente válidos.
En el diagrama de Talagrand del ejemplo anterior, los datos son pronósticos por conjuntos de las alturas a 500 hPa de 120 horas del NCEP para todos los puntos de malla de la región extratropical del hemisferio norte entre abril y junio de 1999. Debido a que el SPC contiene 17 miembros, hay 18 clases. En teoría, cada clase debería contener 1/18 de las verificaciones (el 5,56 %), que aquí provienen de los análisis del sistema de pronósticos globales del NCEP. La frecuencia teórica está marcada con la línea azul.
En este caso, se observa fácilmente que hay más verificaciones de lo esperado por debajo de los rangos de los miembros del conjunto más bajo y segundo más bajo, y arriba del más alto y del segundo más alto. Hay menos verificaciones de lo esperado en todas las demás clases entre estos extremos. ¿Cómo podemos interpretar este resultado en términos de la confiabilidad de la predicción por conjuntos?
Interpretación de los diagramas de Talagrand
Los cuatro paneles siguientes representan cuatro distribuciones de frecuencia hipotéticas relativas a categorías de pronóstico. La línea teórica de confiabilidad perfecta se muestra con una línea horizontal en todos los paneles. Debajo de cada diagrama se muestra la interpretación correspondiente. Los ejemplos muestran diagramas para SPC con dispersiones excesivamente grandes y pequeñas, y con sesgos altos y bajos.
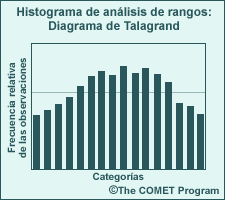
Dispersión excesivamente grande del conjunto. La frecuencia de las observaciones es más baja de lo esperado en los extremos y más alta de lo esperado en el rango medio de los pronósticos.
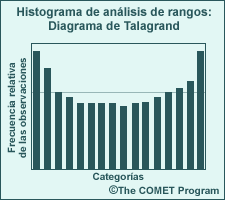
Dispersión excesivamente pequeña del conjunto. La frecuencia de las observaciones es más alta de lo esperado en los extremos y más baja de lo esperado en el rango medio de los pronósticos.
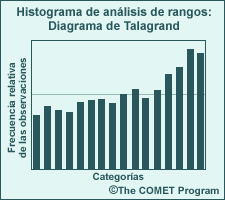
Sesgo bajo del conjunto. La frecuencia es más baja de lo esperado para las observaciones bajas y más alta de lo esperado para las observaciones altas.
Sesgo alto del conjunto. La frecuencia es más alta de lo esperado para las observaciones bajas y más baja de lo esperado para las observaciones altas.
Cabe hacer algunas advertencias que conviene tener presente al interpretar los diagramas de Talagrand:
- existe el potencial de que la media del conjunto suavice los sesgos dependientes del régimen al crear las categorías o rangos;
- el error en las observaciones o un muestreo imperfecto puede crear distribuciones de frecuencias engañosas;
- si no hay sesgo, debe esperarse un diagrama de Talagrand plano para un pronóstico de largo plazo, algo que resulta inútil en la práctica, ya que simplemente indica que el SPC coincide con la climatología, y eso no nos brinda información útil sobre la confiabilidad.
A fondo: tenga cuidado
Las siguientes son algunas advertencias relacionadas con la interpretación de los diagramas de Talagrand (histogramas de rangos).
- Un histograma de rangos plano no garantiza la confiabilidad del SPC. Las siguientes
situaciones de baja confiabilidad pueden también producir histogramas planos:
- sesgos asociados a diferentes regímenes en las predicciones por conjuntos generados
por el SPC en el período del estudio, que al ser promediados crean un histograma
plano;
- error de muestreo, incluidas las observaciones de muestras dependientes del espacio.
- sesgos asociados a diferentes regímenes en las predicciones por conjuntos generados
por el SPC en el período del estudio, que al ser promediados crean un histograma
plano;
- Los histogramas de rangos planos pueden también indicar que el conjunto está especificando
correctamente la varianza en un punto de malla, pero las covarianzas pueden todavía no estar
especificadas correctamente. Esto se puede comprobar en cierta medida generando histogramas
de rangos para diferencias entre valores en diversos puntos de malla o usando otros
diagnósticos.
- Un histograma de rangos con forma de «U», que suele interpretarse como indicador
de falta de variabilidad en el conjunto, puede también ser un signo de diferencias en los
sesgos de diferentes regímenes del flujo. Para determinar si esto es posible, se generan
histogramas de rangos para subpoblaciones para determinar si la forma varía de una a otra;
esto puede proporcionar una cierta perspectiva para determinar si la forma de U indica
sesgos dependientes del régimen de flujo o muy poca variabilidad.
- Las observaciones imperfectas se utilizan comúnmente para el valor de verificación en la
generación del histograma de rangos. Si no tomamos en cuenta los errores de observación,
pueden afectar a la forma del histograma de rangos; cuanto mayor el error, tanto más
acentuada será su forma de «U», aun cuando el conjunto sea confiable. Si se
conocen las características del error en las observaciones, este problema se puede corregir
agregando ruido aleatorio a cada miembro del conjunto de forma coherente con las
estadísticas del error en las observaciones.
- Cuando se prueban los datos del conjunto en lo que respecta a la uniformidad de los histogramas de rangos en el tiempo y el espacio, las muestras empleadas para crear los histogramas de rangos deben estar suficientemente separadas unas de otras (espacial y temporalmente) como para considerarse independientes entre sí.
Aplicaciones
Aplicación al SPC del NCEP
La verificación del SPC del NCEP está disponible prácticamente en tiempo real en la página web de evaluación del conjunto global. Los ejemplos de verificaciones del SPC con el diagrama de Talagrand que aparecen a continuación corresponden a los períodos de mayo a julio de 2002, y de diciembre de 2002 a febrero de 2003.
La animación que aparece más adelante presenta un diagrama de Talagrand para el período entre las 0000 UTC del 22 de febrero y las 0000 UTC del 8 de abril de 2003 que corresponde a los pronósticos del SPC de las alturas de 500 hPa de uno a siete días sobre el hemisferio norte (20 a 80°N). Cada cuadro agrega un día al pronóstico del SPC. Para un SPC perfectamente confiable durante este período, el valor esperado para todas las clases sería cerca del 9,09 % (puesto que hay 11 clases entre, debajo y sobre los 10 miembros del conjunto de las 0000 UTC). ¡Recuerde las advertencias acerca del uso de los diagramas de Talagrand!
Observe que el día uno las clases de 5 a 8 exceden el valor esperado, mientras que todas las demás son inferiores al valor esperado de 9,09 %. Esto es común temprano en la predicción por conjuntos a mediano plazo (Medium-Range Ensemble Forecast, o MREF) y en general se puede atribuir a la dispersión excesiva en las perturbaciones iniciales del pronóstico. Para el MREF, se quiere la mejor dispersión en las salidas de los pronósticos a mediano plazo, de modo que las perturbaciones iniciales se diseñan para dar los mejores resultados en el período de 4 a 15 días. Para los días uno a tres, se deben usar los SPC diseñados para la predicción por conjuntos a corto plazo (Short-Range Ensemble Forecasting, o SREF).
Para el día dos, el pico que vemos en la clase 6 se dispersa, y ahora hay más miembros en los extremos de la distribución. También observamos que la clase superior (es decir, para verificaciones más altas que los 10 miembros clasificados del conjunto) ya es mayor que el valor esperado. La dispersión de la distribución y la tendencia de las verificaciones a bajar en la parte superior de los rangos de los miembros del conjunto continúan hasta el día 7. Sin embargo, solamente para los pronósticos del día siete encontramos que algunas de las clases del extremo inferior exceden el valor esperado, y solo para la clase inferior (es decir, verificaciones por debajo del miembro más bajo del conjunto).
Comparación de la eficiencia del SPC de otros centros meteorológicos
Este segundo ejemplo de aplicación presenta una comparación de la confiabilidad del funcionamiento del SPC en diversos centros meteorológicos. Las tablas de la próxima sección muestran los diagramas de Talagrand para el verano de 2002 y el invierno de 2002-03 en el hemisferio norte (20-80°N) para tres centros meteorológicos [de izquierda a derecha: el NCEP, el Centro Meteorológico Canadiense (CMC), y el Centro Europeo (ECM)]. Estas verificaciones se pueden encontrar casi en tiempo real en las páginas web del NCEP (en inglés). Cada centro utiliza diferentes métodos para crear los miembros de sus conjuntos, tiene un número diferente de miembros del conjunto y utiliza modelos con diferente resolución, métodos numéricos, parametrizaciones físicas y características de error. La frecuencia relativa expresada como porcentaje aparece en el eje X; las categorías aparecen en el eje Y. Las categorías están en grupos de 11. Para los sistemas de conjuntos con más de 10 miembros, se han agrupado las categorías contiguas para crear 11 categorías iguales. El intervalo del porcentaje es del 3 %. De arriba abajo, los diagramas corresponden a los pronósticos de 1 día, 3 días, 5 días, 8 días y 10 días.
Las interpretaciones de los diagramas de cada centro meteorológico aparecen en una lista debajo de cada tabla. Los comentarios suponen un comportamiento de frecuencia igual sobre todo el dominio.
Datos de verificación, verano de 2002
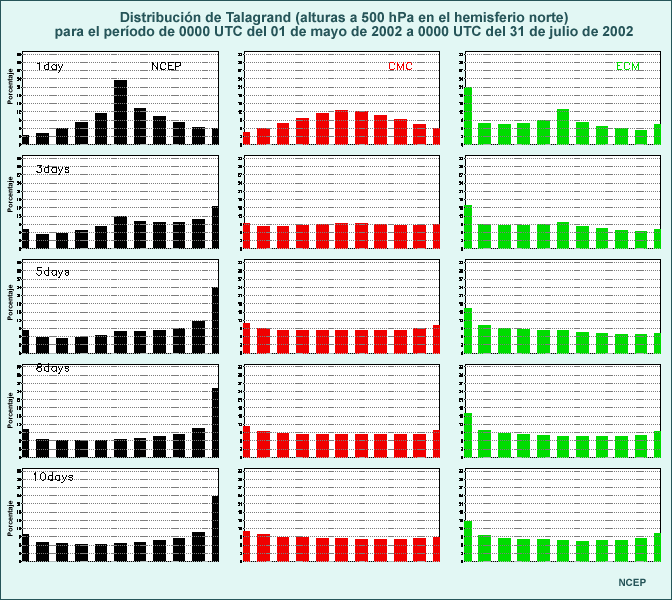
Comentarios para el verano de 2002:
- NCEP: dispersión excesiva al comienzo que disminuye con el tiempo en relación a la verificación. Sesgo bajo evidente a partir del día 3 (el pico a la derecha). Para el día 8, el 24 % de las verificaciones son más altas que todos los miembros del conjunto.
- CMC: tiene la mejor dispersión inicial. Incluso para el día 3 la distribución es aproximadamente uniforme, con una dispersión un poco escasa más adelante. Leve tendencia al desplazamiento hacia un sesgo alto.
- ECM: demasiados miembros altos (el pico a la izquierda). El pico secundario en el centro de la distribución desaparece para el día 5. La dispersión decrece lentamente con el tiempo; hay indicaciones de muy poca dispersión (picos leves en ambos lados).
Invierno de 2002-03
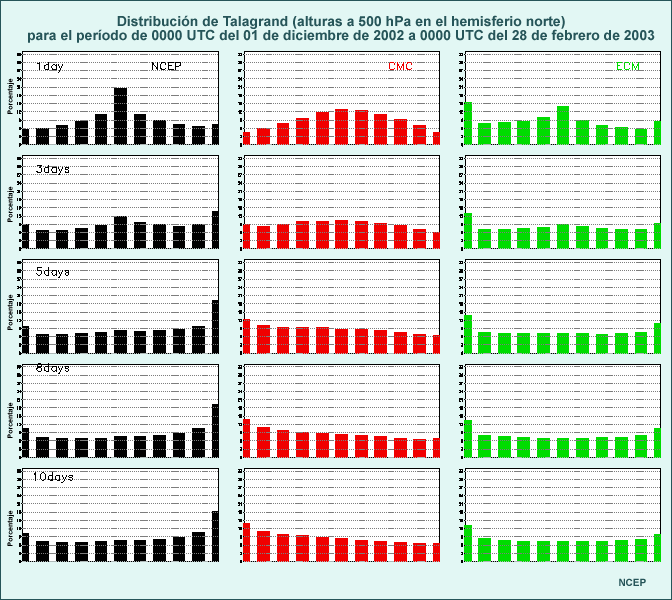
Comentarios para el invierno de 2002-2003:
- NCEP: dispersión excesiva al principio (pico central) que disminuye con el tiempo. Sesgo evidente hacia alturas bajas desde el día 3 (pico a la derecha). Más del 18 % de las verificaciones son más altas que todos los miembros del conjunto para el día 5. Sin embargo, la distribución total en los días 5-10 parece ser un poco mejor que para el verano de 2002, con más verificaciones en el medio de la distribución.
- CMC: tiene la mejor dispersión inicial. El sesgo hacia alturas altas (pico creciente a la izquierda) es más significativo aquí que para el verano de 2002, ya que muestra un sesgo inicial en la distribución del día 3 (cuando la distribución del verano de 2002 indicaba un alto grado de confiabilidad). El sesgo hacia alturas altas aumenta entre los días 3 y 8, y parece estabilizarse entre el día 8 y el día 10.
- ECM: sesgo hacia alturas altas el día 1 (pico a la izquierda) que declina lentamente, con un mejor desempeño en este respecto que para el verano. El pico secundario en el centro de la distribución desaparece para el día 5. La dispersión disminuye con el tiempo en relación con la verificación y, en general, parece un poco demasiado pequeña.
Las diferentes características de confiabilidad de cada SPC son obvias, incluso cuando se utiliza una sola técnica de verificación. Observe cómo la confiabilidad se ve afectada por el modelo subyacente empleado para crear los miembros del conjunto. Por ejemplo, el SPC del NCEP muestra claramente el sesgo hacia alturas bajas del modelo GFS subyacente.
Ejercicios
Interpretación de los diagramas de Talagrand
Pregunta
Después de revisar los diagramas de Talagrand y su cambio conforme se desarrolla la predicción por conjuntos, ¿cómo interpretaría la tendencia en los diagramas de Talagrand para los pronósticos de uno a siete días del período del 22 de febrero al 8 de abril? Marque las opciones que le parecen correctas. Para cambiar una respuesta, vuelva a hacer clic en ella.
Las respuestas correctas son a) y c).
La respuesta a) es correcta, porque el número de verificaciones que cae fuera del rango de los valores del conjunto (es decir, las probabilidades totales en las categorías más bajas y más altas) llega a exceder el valor esperado alrededor del día 4. La respuesta b) es incorrecta debido a que un sesgo bajo en la altura de 500 hPa, según lo indicado por la tendencia de los diagramas de Talagrand, indicaría temperaturas entre el nivel de 500 hPa y la superficie (en equilibrio hidrostático) excesivamente bajas en el modelo. Por consiguiente, la respuesta c) es correcta. La respuesta d) es incorrecta porque la distribución no indica nada sobre humedad, disturbios u ondas en el nivel de 500 hPa.
Es importante recordar, sin embargo, que si hubiera habido una distribución uniforme entre las categorías, eso no garantizaría la confiabilidad a menos que el comportamiento de la distribución fuera coherente en todas las áreas de las cuales provienen los datos.
Interpretación de los diagramas de confiabilidad
El diagrama de confiabilidad que aparece a continuación fue tomado del sitio web de verificación del índice de calor del Centro de Predicción Hidrometeorológica (Hydrometeorological Prediction Center, o WPC) del NCEP, y corresponde a los pronósticos de 4 días para el período entre el 1º de mayo y el 30 de septiembre de 2003 del WPC (llamado MEDR DESK en el producto) y el modelo GFS de pronósticos por conjuntos a mediano plazo (MREF). El umbral de índice de calor que estamos evaluando es el de 35 °C. El eje X representa el centroide de las probabilidades pronosticadas para un índice de calor de 35 °C o más (un centroide de 0,05 representa probabilidades entre 0 y 0,10) y el eje Y las frecuencias observadas asociadas. La diagonal representa una confiabilidad perfecta. Este tipo de diagrama de confiabilidad combina las curvas de confiabilidad y n histograma de frecuencia en una gráfica. Es decir, las columnas coloreadas en este diagrama son similares a las del pequeño histograma incluido debajo del diagrama de confiabilidad que mostramos antes. En este caso, las columnas indican porcentajes de frecuencias para cada probabilidad del pronóstico, en lugar del número de pronósticos, y de este modo pueden compartir los ejes con las curvas de confiabilidad.
Pregunta
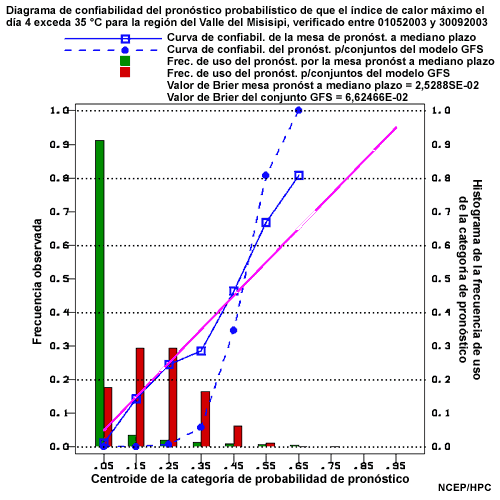
De acuerdo con este diagrama de confiabilidad, ¿cuáles de las afirmaciones siguientes son válidas? Elija todas las opciones pertinentes.
Las respuestas correctas son a) y c).
Las columnas del histograma muestran que más del 90 % de los pronósticos del WPC se encuentran en los rangos de probabilidad de 0 a 0,1 (la columna verde a la izquierda), mientras que el 60 % de las predicciones por conjuntos a mediano plazo (MREF) del modelo GFS caen en el rango de 0,1 a 0,3 (segunda y tercera columnas rojas). El rango de resolución de la predicción por conjuntos a mediano plazo del GFS es de cerca 0,01 a 1,0 (con una probabilidad de pronóstico de 0,65, siempre se alcanzó el umbral de 35 °C), mientras que el de los pronosticadores del WPC es de cerca de 0,01 a aproximadamente 0,81 (con una probabilidad de pronóstico de 0,65, había un 0,81 de probabilidad de satisfacer el umbral de 35 °C).
Recuerde que cuanto más confiable sea el pronóstico, más cercana estará su curva de confiabilidad a la diagonal. Por consiguiente, la respuesta a) es correcta y la respuesta b) incorrecta.
La posición de la curva de confiabilidad frente a la diagonal indica si hay sesgo hacia un pronóstico subestimado (por encima de la diagonal, donde la frecuencia observada es mayor que la probabilidad pronosticada) o hacia un pronóstico exagerado (o debajo de la diagonal, donde la frecuencia observada es menor que la probabilidad pronosticada). Por lo tanto, la respuesta c) es correcta, mientras que d) es incorrecta.
Interpretación de las características operativas relativas
El siguiente diagrama de las características operativas relativas (Relative Operating Characteristics, o ROC) proviene del NCEP y representa una forma de verificar los pronósticos de 5 días de las alturas de 500 hPa, de abril a junio de 1999 para la predicción por conjuntos a mediano plazo (Medium-Range Ensemble Forecast, o MREF) del GFS del NCEP y un ciclo de control de mayor resolución del modelo GFS. A los fines de este ejercicio, el índice de aciertos se define como la fracción del total de pronósticos "sí" correctos sobre el total de pronósticos "sí". El índice de falsas alarmas o probabilidad de detección falsa se define como los pronósticos "sí" incorrectos como fracción del total de observaciones "no".
Pregunta

De acuerdo con este diagrama ROC, ¿cuáles de las afirmaciones siguientes son correctas? Elija todas las opciones pertinentes.
Las respuestas correctas son a) y c).
En el diagrama ROC anterior, la línea diagonal marca la línea de habilidad cero (donde son iguales los aciertos y las falsas alarmas). Cualquier pronóstico con una curva ROC que esté por encima o por debajo de esta línea no tiene ninguna habilidad.
Esto significa que tanto el pronóstico de control de alta resolución del modelo GFS como el del MREF exhiben habilidad. Por lo tanto, las respuestas b) y d) son incorrectas y a) es correcta. La curva roja representa el conjunto del MREF y si miramos el índice de aciertos de 0,76 en esa línea, podemos ver que el índice de falsas alarmas se aproxima a 0,47. Por lo tanto, la respuesta c) es correcta.
Ejemplos de aplicación
Ahora que ha terminado de estudiar la lección, puede tomar la prueba de la lección para evaluar rápidamente lo que aprendió sobre las predicciones por conjuntos.
Para estudio adicional y para demostrar el uso de los productos del sistema de predicción por conjuntos en el proceso de pronóstico, esta sección incluye una serie de ejemplos cortos basados en la web. Dichos casos de estudio se encuentran en el sitio web Applications of NWP Concepts (Aplicaciones de los conceptos de PNT), una colección de breves casos de estudio que muestran cómo y cuándo utilizar, no utilizar o modificar los productos de PNT en el proceso de pronóstico. Proporcionamos estos enlaces para su conveniencia, con el fin de que pueda encontrar fácilmente algunos casos particularmente apropiados para esta lección. Aunque es posible que algunos enlaces aún no estén en funcionamiento, lo estarán próximamente, conforme se vayan publicando. Agregaremos a los ejemplos situaciones de pronóstico de interés que nos lleguen por correo electrónico y a través de los grupos de noticias u otros medios de contacto con el equipo de la serie de lecciones de desarrollo profesional sobre PNT.
| Ejemplos de invierno |
Descripción
|
| Pronóstico por conjuntos a corto plazo para la tormenta de hielo del 4-5 de diciembre de 2002 en Carolina del Norte |
Este ejemplo de principio del invierno muestra el uso del sistema de predicción por conjuntos a corto plazo (Short-Range Ensemble Forecast, o SREF) antes de una tormenta de invierno en Carolina del Norte. El ejemplo muestra la incertidumbre de la trayectoria de la tormenta, la profundidad e intensidad del aire frío empozado, el momento del pronóstico cuantitativo de precipitación (PCP) y el tipo de precipitación. Nota: este ejemplo contiene enlaces a material didáctico sobre los productos del sistema de predicción por conjuntos usados. |
| SREF, condiciones iniciales y la tormenta de nieve del noreste de EE. UU. del 6-7 de enero de 2002 |
Este ejemplo presenta la incapacidad del sistema de predicción por conjuntos a corto plazo (Short-Range Ensemble Forecast, o SREF) de capturar un episodio de nieve importante que ocurrió en los estados del interior a norte del Atlántico Medio y de Nueva Inglaterra, en EE. UU., el 6 y 7 de enero de 2002. Aunque este es un ejemplo de invierno, lo que aprenda de este caso de estudio se aplica al uso del SREF en cualquier época del año. |
| Pronóstico por conjuntos a corto plazo para la tormenta de nieve en Washington D.C. del 5-6 de diciembre de 2002 |
Este ejemplo de principio del invierno muestra el uso del sistema de predicción por conjuntos a corto plazo (Short-Range Ensemble Forecast, o SREF) antes de una tormenta de invierno en el área de Washington D.C. El ejemplo muestra la incertidumbre en la trayectoria de la tormenta, la profundidad e intensidad del aire frío empozado, el momento del pronóstico cuantitativo de precipitación (PCP) y el tipo de precipitación. |
| Uso de la predicción por conjuntos a mediano plazo para evaluar posibles eventos de clima invernal |
La resolución gruesa de las predicciones por conjuntos a mediano plazo
(Medium-Range Ensemble Forecast, o MREF) acoplados con la impredictibilidad
de los fenómenos de pequeña escala en rangos de tiempo grandes generalmente (aunque
no siempre), limita el uso de los MREF a «advertirnos» de la posibilidad
de que se produzcan eventos meteorológicos importantes. |
| Un evento de precipitación intensa en el oeste de los Estados Unidos, noviembre de 2001 | De próxima publicación... |
| Ejemplos de tiempo severo | |
| Tiempo severo en las planicies del sur de EE. UU., abril de 2002 | De próxima publicación... |
| Episodio de tiempo severo en las planicies centrales de EE. UU., mayo de 2003 | De próxima publicación... |
| Ejemplo general | |
| Interpretación de los vuelcos del pronóstico del modelo global |
Los que pronosticamos el tiempo ya estamos familiarizados con los cambios ocasionales que se producen entre un ciclo de ejecución y otro en la dirección dada por los pronósticos de mediano plazo (y a veces incluso los de corto plazo) del modelo de pronóstico global (conocido como AVN/MRF). Este caso de estudio describe dos vuelcos del modelo en un par de ciclos de ejecución del modelo operativo de pronóstico de mediano plazo en dos pasadas adyacentes y muestra cómo las predicciones por conjuntos de mediano plazo aclaran lo que realmente está sucediendo en las estaciones del modelo MRF operativo. |
Colaboradores
Patrocinadores
- Air Force Weather Agency (AFWA)
- Meteorological Service of Canada (MSC)
- NOAA National Environmental Satellite, Data and Information Service (NESDIS)
- Naval Meteorology and Oceanography Command (NMOC)
- National Oceanic and Atmospheric Administration (NOAA)
- National Polar-orbiting Operational Environmental Satellite System (NPOESS)
- National Weather Service (NWS)
Principales asesores científicos
- Dr. Steve Tracton — Office of Naval Research (ONR)
- Dr. Zolton Toth — NCEP
Asesores científicos adjuntos
- Dr. Ralph Petersen — Universidad de Wisconsin, Madison
- Pete Manousos — NCEP/Hydrological Prediction Center
Jefes del proyecto
- Dr. William Bua — UCAR/COMET
- Bonnie Slagel — UCAR/COMET
Meteorólogo del proyecto
- Dr. William Bua — UCAR/COMET
- Dr. Stephen Jascourt — UCAR/COMET
Diseño instruccional
- Patrick Parrish — UCAR/COMET
Diseño multimedia
- Bonnie Slagel — UCAR/COMET
- Carl Whitehurst — UCAR/COMET
Diseño de interfaz gráfica/Ilustración
- Heidi Godsil — UCAR/COMET
Ilustración/Animación
- Steve Deyo — UCAR/COMET
- Heidi Godsil — UCAR/COMET
Pruebas de software/Control de calidad
- Linda Korsgaard — UCAR/COMET
- Michael Smith — UCAR/COMET
Administración de derechos de autor
- Lorrie Fyffe — UCAR/COMET
Datos cortesía de:
- NCEP
Equipo de integración HTML de COMET, 2020
- Tim Alberta — Gerente del proyecto
- Dolores Kiessling — Jefa del proyecto
- Steve Deyo — Diseñador gráfico
- Gary Pacheco — Jefe de desarrollo web
- Justin Richling — Desarrolladora web
- David Russi — Traductor
- Gretchen Williams — Desarrolladora web
- Tyler Winstead — Desarrollador web
Personal de COMET: septiembre 2004
Director
- Dr. Timothy Spangler
Subdirector
- Dr. Joe Lamos
Jefe del Grupo de Recursos Meteorológicos
- Dr. Greg Byrd
Gerenta comercial/Supervisora administrativa
- Elizabeth Lessard
Administración
- Lorrie Fyffe
- Heather Hollingsworth
- Bonnie Slagel
Producción de gráficos/multimedia
- Steve Deyo
- Heidi Godsil
- Seth Lamos
- Dan Riter
Soporte de hardware/software y programación
- Tim Alberta (Supervisor)
- James Hamm
- Karl Hanzel
- Andrew Jurey (Estudiante)
- Ken Kim
- Mark Mulholland
- Carl Whitehurst
Diseño instruccional
- Patrick Parrish (Supervisor)
- Dr. Alan Bol
- Lon Goldstein
- Bryan Guarente
- Dr. Vickie Johnson
- Bruce Muller
- Katherine Olson
- Dwight Owens
- Dr. Sherwood Wang
Meteorólogos
- Dr. William Bua
- Patrick Dills
- Tom Dulong
- Kevin Fuell
- Patrick Hofmann (Estudiante)
- Dr. Stephen Jascourt
- Matthew Kelsch
- Dolores Kiessling
- Heather McIntyre (Estudiante)
- Wendy Schreiber-Abshire
- Dr. Doug Wesley
Pruebas de software/Control de calidad
- Michael Smith (Coordinador)
National Weather Service, Sucursal COMET
- Anthony Mostek (Jefe [interino] de la sucursal COMET del NWS y Jefe de Entrenamiento Satelital)
- Dr. Richard Koehler, Hydrology Training Lead
- Brian Motta
- Dr. Robert Rozumalski (Coordinador de SOO Science and Training Resource [SOO/STRC])
Meteorólogos visitantes del Servicio Meteorológico de Canadá
- Peter Lewis
- Garry Toth
Traducción al español
- David Russi