

When the model run starts with a new analysis, imbalances in the initial conditions cause gravity wave noise early in the forecast and an adjustment of the large-scale fields. This is described on the previous page. It is why most analyses apply some sort of balance constraint and why an initialization procedure may be run following the analysis.
At this point you may want to use this clickable diagram in the COMET module, Understanding Data Assimilation, as a refresher on the terminology and process of converting observations to observation increments (difference between observations and the first guess forecast) and analyzing those into analysis increments (differences between the analysis and the first guess forecast).
For models with an assimilation cycle (such as the operational Eta in 2002,
but not the nested higher-resolution runs), the forecast impact of new data
is the model's response to the analysis increments (changes from
the first guess). Thus, what matters is whether the analysis increments are
primarily in the wind field or the mass field and whether they are large or
small in scale compared to our favorite length scale, 2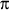 LR.
This means:
LR.
This means:
In the tropics, the forecast can be most improved with wind observations
In middle latitudes, the large-scale forecast winds will be determined largely by the initial mass field, making temperature observations most important
Moisture observations don't create much dynamic adjustment by themselves
but are linked to both mass and wind changes through the model integration
during the assimilation period, during which the model evolution is affected
by changes in radiation and latent heating in model precipitation
How the data are put into the model makes a huge difference
Forcing the analysis to tightly fit observations, especially of pressures/heights/temperatures, in a small region around the observation will not have much lasting impact on the forecast and may produce adjustment toward an incorrect large-scale state, resulting in degradation after some time into the forecast
Mesoscale data assimilation is a major challenge, and getting consistent
forecast benefit beyond a few hours from assimilating mesoscale observations
is extremely difficult
Forecast impacts of analysis correlation lengths
The scale of analysis increments, and thus their impact on the subsequent model forecast, depends heavily on some details of the analysis method rather than just depending on the scale of observed features or the observation spacing.
Statistical analysis systems, including 3D-VAR, assume that there is some relationship between corrections required to the first guess (also called "background") some distance from an observation and the correction required at that observation location. This relationship, properly expressed as forecast error covariances (also called "background error covariances") is characterized with a correlation length, which is a distance over which the relationship extends. To review how 3D-VAR works, refer to the COMET module, Understanding Data Assimilation, especially the graphic explaining background error covariances. Correlating the correction to the first guess over some distance produces smoothing of the analysis increments. Both vertical and horizontal relationships are used, so there is effectively some smoothing in both the vertical and horizontal. Typically, correlation lengths will be longer for coarser resolution models, meaning small-scale features poorly depicted in the first guess field will show up at larger scales in the analysis than in reality.
The horizontal correlation length affects the horizontal scale at which information from observations enters the analysis. If this length scale is large, only synoptic-scale features will be changed by observations, and the mass observations will be most critical to the forecast. If the correlation length is short, then wind observations become more important because the analysis increments will involve more small-scale structure.
The vertical correlation length affects the depth through which observations influence the analysis, and thus the Rossby radius of features in the analysis increments. If the vertical correlation length is short, then the Rossby radius will be smaller, making mass observations more useful.
Remember, the analysis comes from adding the analysis increments to the first guess. Thus, detailed structure in the first guess forecast will get passed along to the analysis if the influence of observations is smoothed to coarser vertical and horizontal scales.
Assimilation of high-resolution observations in high-resolution models
This subject is explored through some challenging questions on a special advanced subtopics page. The content on that page is not tested in the exercises at the end of this module or in the LMS exam. You are encouraged to let your curiosity get the best of you and try it — even if you don't select the correct answers, you will learn from the discussion. Before proceeding, make sure you understand the concept of correlation length explained above, then continue to the special advanced subtopics page.
![]()