Navigation bar

How large is "large scale?" Depth, stability, and vorticity matter

How large is 2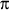piLR? That depends primarily on the vertical depth of the disturbance and to a lesser degree on the lapse rate and absolute vorticity. The first two of these factors enter the picture because they affect the gravity wave speed. The third enters because it affects the inertial time scale. Also, 2piLR is much larger in the tropics because the small Coriolis parameter there makes the inertial period much longer than in midlatitudes.

2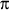piLR  =  gravity wave speed  x  inertial period

Gravity Wave Speed         Inertial Period         Practical Examples

How fast is the gravity wave speed?

Practical impact

External wave:
An external wave extends through the depth of the entire atmosphere, like a tsunami does in the ocean. Depending on the model top height, a model may generate an external wave traveling at several hundred meters per second!

This makes 2piLR on the order of 10,000 km! Some information about the disturbance is spread very far, very rapidly. Only the disturbance winds have lasting impact; the disturbance thermal anomalies vanish.

Internal wave:
The gravity waves of greatest practical importance are internal waves. These include things like mountain waves and the waves that you see in some cloud streets and in raw (not time-averaged) profiler data.

A disturbance described by a hump-shaped perturbation profile leads to a gravity wave of "equivalent depth" 2H, where H is the depth of the hump. Such an internal wave has a group velocity (energy propagation) of speed

N H over pi
where N is the Brunt-Vaisala frequency.

lapse rate

N at 0°C

dry adiabatic (9.8 K/km)

0 s-1

8 K/km

0.008 s-1

5 K/km

0.013 s-1

isothermal (0 K/km)

0.019 s-1

hump-shaped vertical profile

Hump-shaped perturbation profile

The gravity wave speed is complicated by a variety of additional factors.

A disturbance of depth H generates waves that spread energy outward at speed
cg ~ 3.2 H (N/.01) m/s
where H is given in km and N is in s-1 as in the table to the left.

  • The gravity wave speed, and thus the Rossby radius, increases proportionally with the depth of the disturbance.
  • The gravity wave speed, and thus the Rossby radius, increases with stability by around a factor of two from steep lapse rates to isothermal conditions.

In the real atmosphere, a disturbance of arbitrary shape would generate a complete spectrum of waves — that is, energy is dispersed by waves corresponding to a range of depths instead of just one value of H. The overall broad shape of the disturbance will experience mass and wind field adjustments corresponding to the relatively fast waves associated with the disturbance depth H. The smaller details in the disturbance profile will correspond to thinner, slower waves as though they were weaker disturbances with smaller values of H superimposed on the main disturbance.

  • Broad vertical structure of the disturbance is adjusted with a large Rossby radius
  • Fine vertical structure is adjusted with a small Rossby radius

In a numerical model, only a discrete set of vertical depths is possible, so the adjustment details are slightly different.

2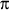piLR  =  gravity wave speed  x  inertial period

How long is the inertial period?

Practical impact

The classic expression for the inertial period, 2pi/f, only applies in the absence of a horizontal pressure gradient. In uniform horizontal shear, square root of eta fsubstitutes for the Coriolis parameter, f, where eta is the absolute vorticity following a parcel (such as on an isentropic surface in unsaturated conditions). For a vortex in solid body rotation, the Rossby radius just uses eta. There is no general formula for more complicated flows, but a generally reasonable approach is to go with

two pi over square root of eta f

Because the absolute vorticity and Coriolis parameter are in the denominator,

  • The Rossby radius is smaller for a cyclone and larger for an anticyclone, typically by a factor of around two compared to average conditions
  • The Rossby radius is larger at lower latitudes, with 20° latitude a factor of two larger than at 45° latitude when the relative vorticity is very small

Putting these pieces together, we find the critical length scale for a disturbance is

two pi L sub R is approximately two pi times the quantity N H over pi all divided by the square root of ata f


which comes out to this most usable form in units of kilometers

two pi L sub R is approximately 200 kilometers times N over 0.01 times H times square root of f nought squared over eta f

where

N

is the Brunt-Vaisala frequency (~.008 s-1 for steep lapse rates of 8 K/km, ~.02 s-1 for isothermal conditions)

H

is the disturbance depth in km

fo

is 10 x 10-5 s -1 (10 "units" on your vorticity map)

f

is the Coriolis parameter (6 x 10-5 s-1 at 25°N, 11 x 10-5 s-1 at 50°N)

eta

is the absolute vorticity

Thus, whether a feature is dynamically "large-scale" or "small-scale" depends on its stability, its depth, and local and planetary contributions of vorticity.

Example

Result

Vortex

  • 200 km in width
  • at latitude 40° N
  • depth of 5 km
  • contains a 40-unit (40 x 10-5 s-1) vorticity maximum
  • moderate lapse rates

The wavelength L is the full crest-trough-crest wavelength, which is around twice the disturbance width. Across this 400 km distance, the average vorticity is much closer to 20 units.

Using 20 units for the vorticity, the formula gives 2piLR ~ 700 km. (H=5, N~0.01 s-1, f~fo, absolute vorticity = 2fo)

400 km << 700 km, so the vortex is "small":

  • Once the forcing that spawned it ends, it will weaken rapidly over a period of hours
  • The mass field will end up in balance with residual weak vortex winds and its influence may spread out some
  • There will be little effect of any sort beyond about 700 km from the vortex center

Suppose the above vortex is filled with a flat cloud deck, the top of which experiences intense radiative cooling. Suppose that

  • the region of intense cooling is 500 m thick
  • the base of the cooled region has steep lapse rates
  • the top of the cooled region has weak lapse rates or even an inversion

The difference between this example and the one above is that now H=0.5 km, giving 2piLR ~ 70 km. (Also, the steep lapse rate near the base of the cooled region further reduces the length scale there, while the opposite affect occurs in the more stable air toward the top of the cooled layer.)

400 km >> 70 km, so this feature is dynamically large:

  • After the clouds dissipate, the cool layer will be retained by the dynamics, though it may get smeared vertically by radiative processes
  • Winds will come into balance with the pancake-shaped cool layer, meaning the vortex will develop a ring of slightly stronger winds above this layer (consider the thermal wind around the edge of the cool region)

Pancake graphic

Remember, this geostrophic adjustment process is in addition to other forcing. As long as a feature is being forced, it will continue to exist, with its structure evolving as determined by the forcing and gradual modification by the adjustment process. Also remember that vertical shear and horizontal deformation can shred a feature over time, even if the dynamics permit a thermal or wind perturbation to otherwise be retained. This is just one more tool in your bag, not the answer to all forecast problems.