The Role of Scale

The key to the response is whether the disturbance is much wider, comparable to, or much less than the Rossby radius of deformation. The Rossby radius is related to the distance a gravity wave propagates before the Coriolis effect becomes important. Essentially, the gravity waves are able to disperse across this distance, as seen by the wiggly height pattern in the middle frame of the animation on the previous page. The gravity waves leave behind an adjusted state, as seen on the last frame, but they are unable to disperse across a broader distance, leaving areas beyond this distance unchanged.

Ways to conceptualize Rossby radius	Consequences
The scale at which rotation becomes as important as buoyancy	Features smaller in scale are dominated by buoyancy forcing, resulting in gravity waves in a stable environment, so they disperse and have a short lifetime Features larger in scale are rotational in character, dominated by Rossby wave dynamics, and have a longer life
The partitioning of potential vorticity (PV) into vorticity (winds) and static stability (mass). (Remember, PV is conserved if potential temperature is conserved. Thus, ignoring latent heating, radiation, and turbulence for the moment, the disturbance PV would be conserved during adjustment.)	A large-scale disturbance primarily causes height and temperature changes to the pre-disturbance state, resulting in the disturbance PV showing up predominantly in the mass field A small-scale disturbance primarily causes vorticity changes to the pre-disturbance state, resulting in the disturbance PV showing up predominantly in the wind field
Partitioning between potential and kinetic energy	A large-scale disturbance ends up with most of its energy stored as potential energy A small-scale disturbance ends up with most of its energy in the form of kinetic energy

The disturbance wavelength (crest-to-crest) L gets compared to .

This (2L_R) is the distance the gravity wave could travel during an inertial period, which, in turn, is the amount of time it would take for an ageostrophic wind vector to completely pivot around a circle as a result of being turned by the Coriolis effect.

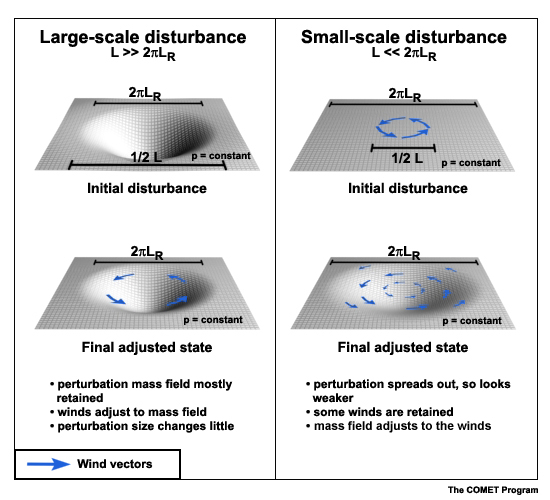
For disturbances of intermediate scale, the result is between these extremes.

The disturbance wavelength (crest-to-crest) L gets compared to . This (2LR) is the distance the gravity wave could travel during an inertial period, which is the amount of time it would take for an ageostrophic wind vector to completely pivot around a circle as a result of being turned by the Coriolis effect. For disturbances of intermediate scale, the result is between these extremes.