Tipo de modelo
Pregunta introductoria
Cuando hablamos de «tipo de modelo», deseamos distinguir entre los modelos espectrales o de malla y los que son hidrostáticos y no hidrostáticos. Estas diferencias influyen en los tipos de errores que produce cada modelo y, por ende, en cómo debemos interpretar el pronóstico que genera. A ver si puede identificar algunas de ellas...
Pregunta
¿Cuáles de los siguientes aspectos se ven afectados por el tipo de modelo? Escoja todas las opciones pertinentes.
Las mejores opciones son (a), (b), (e) y, en menor medida, (d).
Los modelos de malla y espectrales se basan en el mismo conjunto de ecuaciones primitivas. Sin embargo, los dos tipos formulan y resuelven las ecuaciones de manera distinta. Las diferencias en las formulaciones matemáticas básicas producen errores característicos distintos en la guía del modelo.
Las diferencias en las formulaciones matemáticas básicas llevan a diferentes métodos de representar los datos. Los modelos de malla representan los datos en puntos de malla discretos y fijos, mientras que los modelos espectrales utilizan funciones de onda continua. Estas diferencias en la representación de los datos introducen diferentes tipos y cantidades de errores en los análisis y pronósticos.
Juntas, las aproximaciones físicas y dinámicas en las ecuaciones y las características de cada tipo de modelo influyen en el tipo y la escala de las estructuras que un modelo puede representar.
El tipo de modelo no necesariamente afecta la extensión del dominio del modelo. En el pasado hemos usado modelos espectrales porque las funciones de onda y los harmónicos esféricos de la formulación espectral establecen una base matemática natural para un dominio esférico, lo cual permite obtener un alto grado de precisión en el modelado de los movimientos de un fluido sobre una esfera, como ocurre con la atmósfera terrestre. Sin embargo, conforme aumentan los recursos computacionales, los modelos globales convierten paulatinamente en modelos de malla. Normalmente, los modelos no hidrostáticos están limitados a dominios pequeños, porque el costo adicional de calcular los términos no hidrostáticos solo ayuda a pronosticar estructuras de escala pequeña que requieren una resolución muy alta para resolverse y la mayoría de los centros operativos aún no cuentan con suficientes recursos informáticos como para ejecutar un modelo global de alta resolución en tiempo real. No obstante, parece inevitable que en determinado momento las capacidades de cómputo nos permitan ejecutar modelos globales no hidrostáticos.
El tipo de modelo no tiene un impacto directo en la resolución horizontal o vertical seleccionada hasta un espaciado de malla horizontal de aproximadamente 10 km. En teoría, los modelos de malla y espectrales pueden tener cualquier resolución, dentro de las limitaciones de los recursos de cómputo. Sin embargo, los modelos de resolución horizontal muy fina deberían ser no hidrostáticos.
El resto de esta sección explora con mayor detalle las características y los errores asociados con los modelos de malla y espectrales, así como los modelos hidrostáticos y no hidrostáticos.
*Ecuaciones de PNT
Ciertas leyes físicas de movimiento y conservación de la energía (por ejemplo, la segunda ley del movimiento de Newton y la primera ley de la termodinámica) gobiernan los cambios que se producen en la atmósfera. Estas leyes permiten derivar una serie de ecuaciones matemáticas que forman el núcleo de lo que se puede llamar predicción numérica del tiempo.
En 1904, Vilhelm Bjerkness fue el primero en reconocer que la predicción numérica del tiempo era posible, en principio, y propuso que esencialmente el pronóstico del tiempo se puede considerar como un problema matemático de condiciones iniciales: dado un conjunto de ecuaciones que gobiernan el cambio de las variables meteorológicas con el tiempo, si conocemos la condición inicial de la atmósfera podemos resolver las ecuaciones para obtener nuevos valores para esas variables en un momento posterior, es decir, hacer un pronóstico.
Para representar matemáticamente un modelo de PNT en su forma más simple escribimos
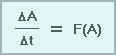
donde:
- ΔA es el cambio en una variable de pronóstico en un punto particular del espacio.
- Δt es el cambio en el tiempo (a qué distancia en el futuro se está pronosticando).
- F(A) representa los términos que pueden causar cambios en el valor de A.
La ecuación se puede expresar en palabras de la forma siguiente:
El cambio en la variable de pronóstico A durante el período de tiempo t es igual a los efectos acumulados de todos los procesos que imponen un cambio en A.
En la predicción numérica del tiempo, los valores futuros de las variables meteorológicas se pueden obtener determinando sus valores iniciales, a los cuales se agrega después el forzamiento físico que actúa sobre las variables durante el período del pronóstico. Esto se puede expresar como

donde F(A) representa la combinación de todos los tipos de forzamiento posibles.
Este proceso se sigue para configurar las ecuaciones de pronóstico utilizadas en PNT. Las ecuaciones de pronóstico específicas usadas en los modelos de PNT se denominan ecuaciones primitivas (no por ser poco elaboradas o simples, sino porque describen los procesos fundamentales que ocurren en la atmósfera). Estas ecuaciones gobiernan el movimiento y los cambios termodinámicos que se producen en la atmósfera y son derivadas de las leyes completas de conservación de momento, masa, energía y humedad.
La forma en que las ecuaciones primitivas se derivan de sus formas teóricas completas y se convierten en código informático puede contribuir a los errores de pronóstico de los modelos PNT.
- Las ecuaciones de pronóstico de los modelos son versiones simplificadas de las leyes físicas que gobiernan los procesos atmosféricos, especialmente los procesos en las nubes, los intercambios entre la tierra y la atmósfera y los procesos de intercambio de radiación. Las aproximaciones físicas y dinámicas de estas ecuaciones limitan los fenómenos que se pueden pronosticar.
- Debido a su complejidad, las ecuaciones primitivas se deben resolver numéricamente, utilizando aproximaciones algebraicas en lugar de calcular soluciones analíticas completas. Estas aproximaciones numéricas introducen errores incluso si las ecuaciones de pronóstico describen completamente los fenómenos de interés y el estado inicial está representado a la perfección.
- Las formas las ecuaciones de pronóstico del modelo empleadas en los equipos informáticos no pueden contener todos los detalles a todas las resoluciones. Por lo tanto, parte de la información sobre los campos atmosféricos faltará o no se representará adecuadamente en el modelo, aunque se cuente con observaciones perfectas y se conozca perfectamente el estado inicial de la atmósfera.
- Los métodos de malla (o cuadrícula) y espectrales son técnicas para representar información acerca de las variables atmosféricas en el modelo y resolver el conjunto de ecuaciones de pronóstico. Cada técnica introduce ciertos tipos de errores.
En el resto de la sección «Tipo de modelo» exploraremos la forma en que los modelos numéricos generan datos de guía para el pronóstico e introducen errores de pronóstico.
*Ecuaciones primitivas
Las cinco ecuaciones siguientes, derivadas del conjunto completo de leyes de conservación de momento, masa, energía y humedad, gobiernan los cambios en el movimiento y la termodinámica de la atmósfera.
Los modelos espectrales de malla emplean el mismo conjunto de ecuaciones para describir los cambios que ocurren en lugares discretos dentro del modelo de pronóstico. Las ecuaciones que aparecen en esta página representan un conjunto simplificado de las ecuaciones que se utilizan en los modelos numéricos. Están escritas en el marco euleriano, en el cual los valores y sus derivadas (cambios a la variable a lo largo del tiempo, por ejemplo, ∂T/∂t o ∂T/∂x) se evalúan en lugares fijos en la Tierra. Las ecuaciones se presentan con coordenadas de presión (x-y-p) y contienen toda la física y la dinámica esencial necesaria para los modelos numéricos, excepto que se han excluido los términos que consideran la curvatura de la Tierra, y los procesos físicos tales como la fricción y el calentamiento adiabático se representan en un solo término en lugar de varios. Como en este ejemplo utilizamos coordenadas de presión, la fuerza del gradiente de presión se expresa como un gradiente vertical (z) y se supone que existe un flujo «horizontal» a lo largo de las superficies isobáricas. (Aunque usamos coordenadas isobáricas en estas ecuaciones simplificadas, la mayoría de los modelos numéricos utilizan otros sistemas de coordenadas verticales para mejorar la exactitud y simplificar los cálculos. Encontrará más información en las secciones Coordenadas verticales y Resolución vertical.)
Para fines de pronóstico, este conjunto de ecuaciones se considera cerrado y completo (lo cual significa que podemos pronosticar valores para todos los términos al resolver cada una de las ecuaciones en la secuencia apropiada) porque:
- todas las ecuaciones utilizan las mismas variables de pronóstico (u, v, ω, T, q, z);
- los términos Fx, Fy, H, E y P también se pueden describir en términos de las seis variables básicas de pronóstico;
- podemos especificar las condiciones iniciales en el dominio del modelo;
- podemos obtener condiciones de frontera apropiadas para todas las variables de pronóstico del modelo.
Las cinco secciones siguientes cubren las ecuaciones individuales.

*Ecuaciones de pronóstico del viento
Componente oeste a este
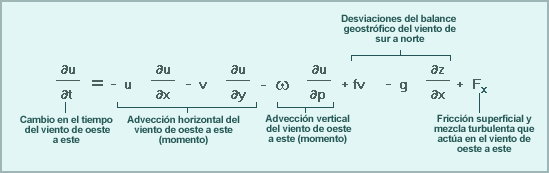
Esta ecuación determina los cambios que se producen con el tiempo en la componente del viento de oeste a este debido a:
- La advección horizontal del viento de oeste a este.
- La advección vertical del viento de oeste a este.
- Las desviaciones del balance geostrófico de la componente del viento de sur a norte. Los desequilibrios entre la fuerza del gradiente de presión de oeste a este y la fuerza de Coriolis que actúa sobre el viento de sur a norte alteran el viento de oeste a este.
- Otros procesos físicos, como la fricción superficial y la mezcla turbulenta que actúan sobre el viento de oeste a este. Los modelos también incluyen aproximaciones empíricas que tratan de representar los procesos atmosféricos que no se pueden pronosticar directamente, aunque algunos de los efectos son indirectos. Por ejemplo, la radiación y la convección se aplican solo a las ecuaciones de temperatura y humedad y no se incluyen explícitamente en las ecuaciones de pronóstico del viento. Sin embargo, los cambios de temperatura que ocurren en un momento dado provocan cambios en el gradiente de presión y en determinado momento esto afectará el viento.
Observe que las dos componentes del viento están interrelacionadas, ya que cada una se ve afectada por los desequilibrios geostróficos de la otra.
Componente sur a norte
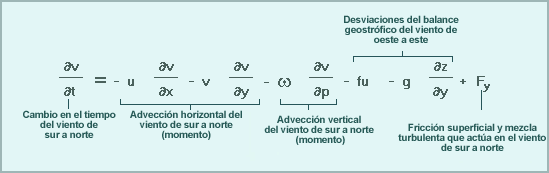
Esta ecuación determina los cambios que se producen con el tiempo en la componente del viento de sur a norte debido a:
- La advección horizontal del viento de sur a norte.
- La advección vertical del viento de sur a norte.
- Las desviaciones del balance geostrófico de la componente del viento de oeste a este. Los desequilibrios entre la fuerza del gradiente de presión de oeste a este y la fuerza de Coriolis que actúa sobre el viento de sur a norte alteran el viento de oeste a este.
- Otros procesos físicos, como la fricción superficial y la mezcla turbulenta que actúan sobre el viento de sur a norte. Los modelos también incluyen aproximaciones empíricas que tratan de representar los procesos atmosféricos que no se pueden pronosticar directamente, aunque algunos de los efectos son indirectos. Por ejemplo, la radiación y la convección se aplican solo a las ecuaciones de temperatura y humedad y no se incluyen explícitamente en las ecuaciones de pronóstico del viento. Sin embargo, los cambios de temperatura que ocurren en un momento dado provocan cambios en el gradiente de presión y en determinado momento esto afectará el viento.
Observe que las dos componentes del viento están interrelacionadas, ya que cada una se ve afectada por los desequilibrios geostróficos de la otra.
Información adicional: fuerza de Coriolis
Para ilustrar un ejemplo conceptual de los efectos de la fuerza de Coriolis, simplificamos la ecuación del viento (momento) suponiendo que los efectos de la advección y la fricción equivalen a cero en una atmósfera inicialmente en reposo. Dado este supuesto, la ecuación se reduce a la siguiente forma.

- Δu/Δt y Δv/Δt son las razones de cambio en las componentes u y v del viento durante el intervalo de tiempo Δt.
- fv y fu representan el efecto de Coriolis.
- (g Δz/Δx y g Δz/Δy) representan las aceleraciones del gradiente de presión en las direcciones x e y, respectivamente (el cambio en z con la distancia).
Inicialmente, suponemos que la Tierra no rota y que no hay radiación solar. Con la atmósfera completamente en reposo, cada uno de los tres términos de la ecuación de momento sería igual a cero. Primero examinaremos los efectos sobre el movimiento de la parcela de aire que ocurren al introducir la radiación solar, y después los que se observan con la rotación de la Tierra. La siguiente discusión se aplica al hemisferio Norte.
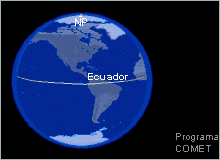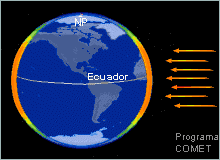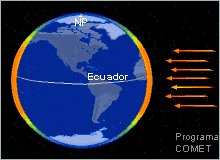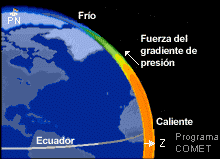
A medida que la radiación solar incidente entra en juego, el ecuador se calienta más que los polos, creando un gradiente de temperatura de sur a norte que decrece hacia el norte, tal como se ilustra en la animación. Debido a que una capa de aire caliente es más gruesa que una capa de aire equivalente más frío y denso, las superficies de presión alcanzan una mayor altura sobre el ecuador que sobre los polos y se produce un gradiente de presión de norte a sur. En la ecuación, el término del gradiente de norte a sur se vuelve
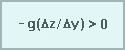
Cuando este término es positivo, se crea una aceleración hacia el norte y esencialmente el aire se mueve por el gradiente de presión de sur a norte (se desplaza cuesta abajo). Esto significa que la componente v del viento es también positiva y una componente v positiva se manifiesta físicamente como un viento del sur.

No hemos considerado aún el efecto de Coriolis. Debido a la rotación de la Tierra, el efecto de Coriolis en la atmósfera real no es cero, salvo en el ecuador. Recuerde que el efecto de Coriolis produce el desvío del aire hacia la derecha en el hemisferio norte (fv > 0).
Si fv > 0, entonces Δu/Δt > 0. Esto indica una aceleración hacia el este, ya que un movimiento u positivo implica una componente de viento del oeste.
Ahora que el viento tiene una componente hacia el este, también debemos considerar el término de Coriolis (fu) en la ecuación 2. En este caso, dado que u > 0, -fu < 0, lo cual reduce la componente del viento hacia el norte.

Esta aceleración negativa reduce la componente sur del viento y, después de varias horas, el viento cambia a norte (v < 0), desviando la parcela de aire hacia el sur. Esta interacción entre las fuerzas del gradiente de presión y el efecto de Coriolis produce una oscilación, que se ilustra abajo.
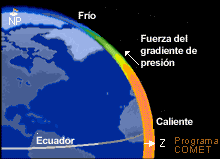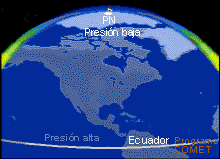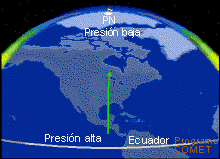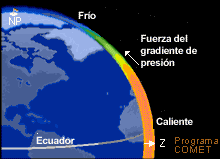
Es importante observar que:
- En este ejemplo, la parcela de aire experimenta oscilaciones inerciales en ausencia de otras fuerzas de gradiente de presión. En la naturaleza, sin embargo, estas oscilaciones se amortiguan rápidamente y se establece un régimen de flujo balanceado.
- Hemos presentado la respuesta atmosférica a una fuerza de gradiente de presión como una serie de eventos seguidos. En la atmósfera real estas respuestas se producen simultáneamente conforme los campos de viento y de presión se ajustan mutuamente y de forma continua.
Información adicional: advección
Esta ilustración representa una situación idealizada para explicar el funcionamiento de la advección de una cantidad por acción del viento.
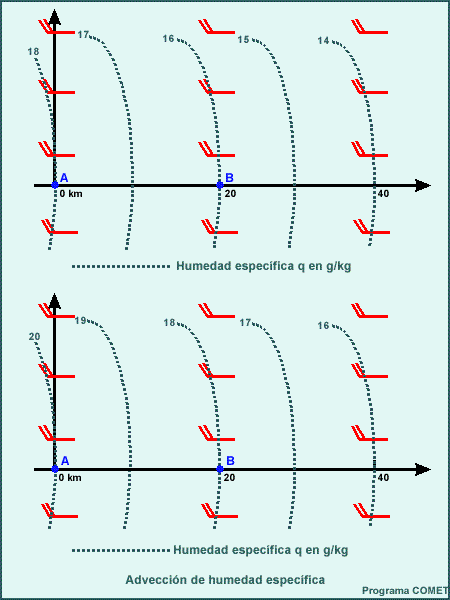
El término de advección determina cómo el valor de una variable en un lugar fijo cambiará solo debido al desplazamiento de un elemento por acción del viento. Por ejemplo, en el momento t = 0, el panel superior muestra los contornos de la humedad específica en fase de aumento asociada con una masa de aire húmedo cerca del punto A y condiciones más secas en el punto B. La velocidad del viento es constante: 20 nudos, de oeste a este. A medida que el viento desplaza este patrón de humedad hacia la derecha con el tiempo, la forma del patrón de humedad permanece igual, pero el patrón se desplaza. El valor de humedad específica en el punto B aumenta conforme la masa de aire húmedo pasa sobre la zona. La cantidad de cambio es directamente proporcional a la intensidad del viento que mueve el patrón de humedad y a la fuerza y ubicación de la variabilidad espacial (gradientes) del campo de humedad.
*Ecuación de continuidad
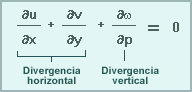
En este ejemplo, la ecuación de continuidad se calcula por diagnóstico a partir del campo de viento horizontal, sin considerar los efectos de empuje hidrostático. La divergencia horizontal se determina a partir de las variaciones espaciales en ambas componentes horizontales del viento. Entonces, la divergencia está relacionada con el cambio en el movimiento vertical desde el fondo hasta la parte superior de una capa dentro del modelo. Las áreas de convergencia horizontal deben coincidir con las áreas en las que el movimiento ascendente aumenta con la altura o en las que el movimiento descendente se debilita con la altura.
La ecuación de continuidad se usa para calcular el movimiento vertical en modelos hidrostáticos. Por otra parte, los modelos no hidrostáticos no utilizan la ecuación de continuidad directamente para calcular el movimiento vertical. En su lugar, utilizan una combinación de divergencia horizontal y empuje hidrostático para determinar los movimientos y las aceleraciones verticales.
*Ecuación de pronóstico de temperatura
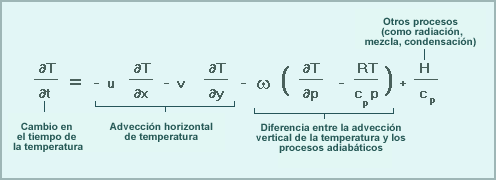
Los cambios de temperatura a lo largo del tiempo están relacionados con:
- La advección horizontal de la temperatura producida por ambas componentes del viento.
- La diferencia entre la advección vertical de la temperatura y el enfriamiento o calentamiento causado por la expansión o compresión del aire ascendente o descendente. Esta componente del cambio de temperatura es proporcional a la intensidad del movimiento vertical y a la diferencia entre el gradiente de temperatura vertical pronosticado y el gradiente adiabático seco.
- El efecto de todos los demás procesos, especialmente la radiación, la mezcla y la condensación, e incluso los efectos de la convección.
Observe la importancia de la velocidad vertical determinada a partir de las ecuaciones de continuidad y de pronóstico del viento. Esta ecuación también depende de la ecuación de pronóstico de la humedad debido al papel de la humedad en el grado de calentamiento y enfriamiento por condensación y en la activación de la convección, que también contribuye al calentamiento y enfriamiento por condensación.
*Ecuación de pronóstico de humedad
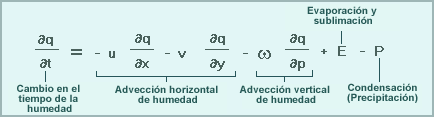
Los cambios de humedad a lo largo del tiempo están relacionados con:
- La advección horizontal de humedad.
- La advección vertical de humedad.
- La evaporación de agua líquida o la sublimación de cristales de hielo.
- La condensación (precipitación). Los modelos utilizan muchas formulaciones complejas para estimar la condensación y precipitación subsiguiente. Note que la conservación de la humedad implica que la precipitación pronosticada por un modelo reduce la cantidad de humedad en la atmósfera del modelo. Por lo tanto, cuando un modelo pronostica incorrectamente la precipitación, la cantidad de humedad corriente abajo se ve afectada.
Observe la importancia de la velocidad vertical determinada a partir de las ecuaciones de continuidad y de pronóstico del viento. También hay una interdependencia entre la ecuación de pronóstico de la temperatura y la cantidad de evaporación que se puede esperar de la superficie terrestre.
*Ecuación hidrostática
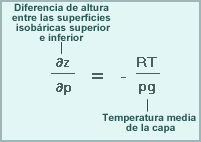
La ecuación hidrostática mantiene la estabilidad dentro del modelo de pronóstico y se utiliza para calcular el campo de altura necesario para determinar el balance geostrófico en las ecuaciones de pronóstico del viento. Esta ecuación de diagnóstico relaciona la temperatura media de una capa del modelo con la diferencia de altura entre las superficies isobáricas superiores e inferiores que representan los extremos superior e inferior de la capa. Las temperaturas obtenidas de la ecuación de pronóstico de temperatura se usan aquí para calcular las alturas, que a su vez se usan en las ecuaciones de pronóstico del viento.
*Ecuaciones de diagnóstico/pronóstico

Las ecuaciones (1a), (1b), (3) y (4) se denominan ecuaciones de pronóstico, porque los cambios que ocurren con el tiempo en las variables de pronóstico (u, v, T, q) se determinan explícitamente por medio de ecuaciones dinámicas. En las ecuaciones (2) y (5), las restantes variables (ω y z) se determinan a partir de las variables de pronóstico. Dado que estas ecuaciones no calculan los cambios que ocurren con el tiempo directamente, se conocen como ecuaciones de diagnóstico.
*Procesos físicos

Todas las ecuaciones de pronóstico deben tratar de considerar los efectos de los procesos que los modelos no pueden pronosticar directamente debido a la complejidad de los procesos físicos que se están simulando (por ejemplo: la radiación) o porque el proceso ocurre sobre escalas demasiado pequeñas para que se pueda incluir directamente en el modelo (por ejemplo: las nubes convectivas). Las aproximaciones empíricas empleadas en las ecuaciones de pronóstico del modelo aparecen en notación abreviada: Fx, Fy, H, E, P.
Fx y Fy (en las ecuaciones 1a y 1b) son los términos de «fricción» que modifican el viento por el rozamiento con la superficie, pero también incorporan otros procesos, incluido el transporte de momento vertical y horizontal por corrientes turbulentas (que suele denominarse difusión en los modelos de gran escala). La «fricción» se ve afectada por el tipo de vegetación (árboles o hierba, por ejemplo), el tipo de superficie (nieve o agua líquida), la temperatura en la superficie y otras condiciones.
El término de calentamiento adiabático H (ecuación 3) incorpora varios procesos: H = HL + HC + HR + HS, donde
- HL es el calentamiento por liberación de calor latente causado por la condensación en el ascenso a gran escala de aire saturado y de estratificación estable, o el enfriamiento debido a la evaporación de la precipitación y del agua superficial;
- HC es el calentamiento por liberación de calor latente producido por la condensación que ocurre en la convección (que a su vez se puede aproximar);
- HR es la tasa de calentamiento radiativo (principalmente en la superficie, en el caso de la radiación solar, y en las capas húmedas de la atmósfera, en el caso de la radiación infrarroja; HR es negativo en caso de enfriamiento radiativo);
- HS representa el flujo de calor sensible hacia y desde la superficie terrestre.
La tasa de precipitación, P = PL + PC (precipitación estratiforme y convectiva), está muy relacionada con HL y HC. Su cálculo depende de ciertos detalles tales como si el modelo pronostica nubes y qué parametrización convectiva o parametrización microfísica se usa.
La evaporación (E) puede provenir del flujo de la humedad que se evapora de la superficie terrestre o la evaporación de precipitación que no llega al suelo.
Hasta ahora, nuestras discusiones han supuesto un flujo sobre una superficie plana. También se deben incluir los efectos de las montañas en el modelo. Dichos efectos se toman en cuenta al seleccionar la coordenada vertical (vea las secciones Coordenadas verticales y Resolución vertical).
El grado en que los modelos numéricos pueden simular la atmósfera real utilizando estas aproximaciones influye directamente en la magnitud del error en el pronóstico del modelo en las áreas donde ocurren estos procesos.
De malla: representación de datos
Para resolver las ecuaciones de pronóstico, la mayoría de los modelos numéricos utilizan datos representados como valores sobre una malla o cuadrícula, o bien en forma espectral. Esta es una representación de puntos de malla. Encontrará una ilustración de una representación espectral en la próxima sección.
En la atmósfera real, la temperatura, la presión, el viento y la humedad varían de un lugar a otro de forma continua y gradual. En esta figura, el campo continuo de temperatura está representado por isotermas rojas, en grados Celsius. Sin embargo, los modelos de malla ejecutan sus cálculos en una matriz fija de puntos de malla que no están conectados en el espacio. Como en realidad los valores de los puntos de malla representan un promedio del área dentro de una celda, el campo continuo de temperatura representado por los tonos azules se debe representar por medio de un solo valor de temperatura, los números negros, en el panel de la derecha.
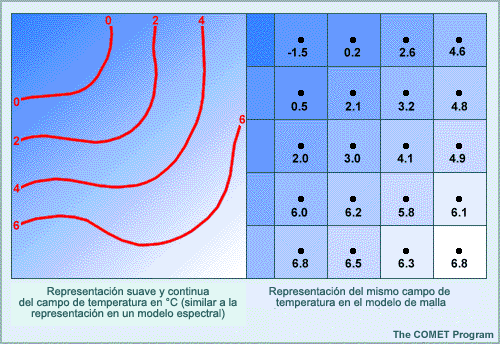
En las ecuaciones de pronóstico, las derivadas se aproximan por medio de diferencias finitas. Por ejemplo, en el lugar donde el valor medio de las celdas de la malla es 0.2, cerca de la parte superior de la figura, el gradiente este-oeste ΔT/Δx, puede usar las celdas contiguas para aproximar la diferencia de temperatura: 2.6 – (-1.5) = 4.1. En este caso el gradiente es 4,1 grados/2Δx. Observe la pérdida de información provocada por este método. Si consideramos los valores de las celdas, podemos apreciar que el gradiente es mayor al este de este punto que al oeste, y sin embargo el gradiente se ha suavizado a través de dos celdas. El hecho de integrar las ecuaciones de pronóstico a lo largo del tiempo introduce otras pérdidas de información, lo cual degrada aún más la representación de las estructuras meteorológicas algunas veces más anchas que el espaciado de la malla. Esto se ilustra conceptualmente en la sección Resolución horizontal.
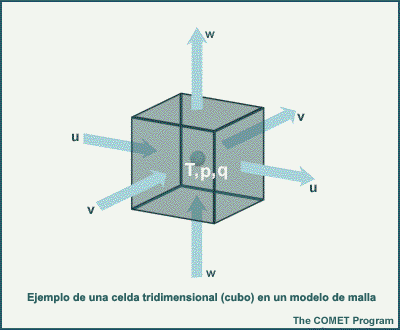
En realidad, los modelos de malla representan la atmósfera en cubos tridimensionales, como el de la figura siguiente. La temperatura, la presión y la humedad (T, p, q) que se indican en el centro del cubo representan el promedio de las condiciones en el interior del cubo. De forma análoga, los vientos de este a oeste (u) y de norte a sur (v), indicados en los lados del cubo, representan el promedio de las componentes del viento entre el centro de este cubo y los cubos adyacentes, y el movimiento vertical (w) está representado en las caras superior e inferior del cubo. Este arreglo de variables en y alrededor del cubo brinda una serie de ventajas a la hora de calcular las derivadas. Además, este esquema es físicamente intuitivo; las propiedades termodinámicas medias del interior del cubo de la malla se representan en el centro, mientras que los vientos en las caras están asociados con los flujos entrantes y salientes del cubo. Cada modelo emplea su propio esquema de malla. La salida del modelo se interpola en sentido vertical y horizontal con una malla común durante el posprocesamiento.
Espectral: representación de datos
Los modelos espectrales representan las variaciones espaciales de las variables meteorológicas (por ejemplo las alturas geopotenciales) como una serie finita de ondas con diferentes longitudes de onda.
Considere el ejemplo del campo hemisférico de alturas de 500 hPa de la parte superior de la figura. Si tabulamos los datos de altura a una latitud de 40°N cada 10 grados de longitud (los puntos amarillos en el mapa), habrá 36 puntos alrededor del globo. Para representar una onda de forma aceptable se requiere un mínimo de cinco a siete puntos y en este caso los datos nos permiten definir cinco o seis ondas. En el mapa, la posición de las vaguadas se muestra con líneas rojas.
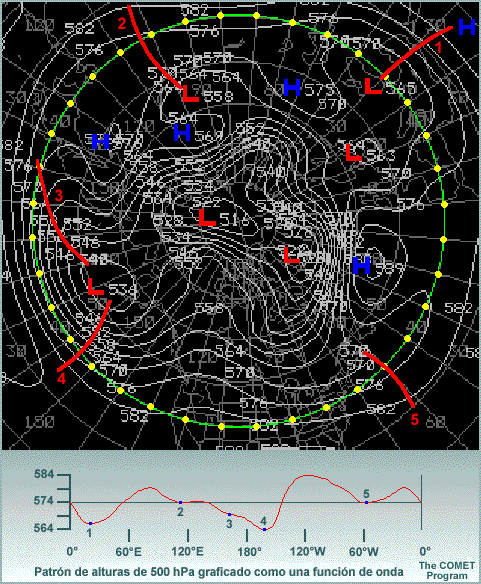
Si trazamos los datos en una gráfica y definimos las cinco vaguadas con puntos azules, vemos que su separación no es uniforme. Esto indica la presencia de variaciones de pequeña escala de más de una longitud de onda. En este caso, las ondas más cortas representan las características de escala sinóptica, mientras que las ondas más largas representan características planetarias.
Como las variables de pronóstico se representan por medio de funciones analíticas continuas, las derivadas horizontales se pueden representar mediante las derivadas de dichas funciones sin que sufran ninguna pérdida de exactitud (suavizado) adicional, como ocurre con las representaciones de malla. Junto con el uso de un paso de tiempo largo, esta ventaja compensa la carga de cómputo que implica transformar las variables de pronóstico en una representación espectral. No obstante, la representación vertical emplea capas discretas, exactamente como en los modelos de malla.
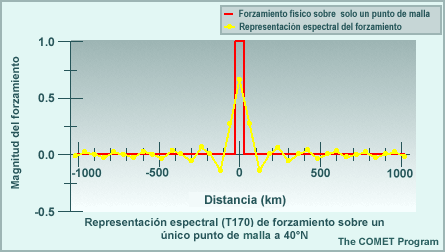
Los modelos espectrales emplean representaciones de malla para calcular las tendencias de las variables de pronóstico en las parametrizaciones físicas. Esto significa que las variables de pronóstico se transforman una y otra vez de una representación espectral para los cálculos de dinámica a una representación de malla para los cálculos de física. El resultado de esta transformación es que los efectos de los procesos físicos se perciben artificialmente a cierta distancia del evento. Por ejemplo, la línea roja en la gráfica siguiente ilustra un evento que ocurre en una sola celda de malla, como puede ser el calentamiento por liberación del calor latente asociado con un foco de precipitación que se produce en una sola columna del modelo. La línea amarilla es la representación espectral de dicho evento. El efecto es la reducción del calentamiento en un 33 % en la celda que contiene la tormenta, y esto luego se propaga a buena distancia en un patrón oscilante. Este ejemplo es para un número de onda máximo de T170 en un lugar cerca de 40°N. Conforme aumentamos el número máximo de ondas, la altura del pico central sube y la oscilación se atenúa más rápidamente con la distancia, de modo que el efecto artificial es más pronunciado a las resoluciones más bajas típicas de los miembros de un conjunto de lo que es el caso con las predicciones «deterministas» individuales de alta resolución.
Cálculos a nivel de malla en modelos espectrales
Para los cálculos de malla, los valores de las variables de pronóstico se deben transformar de la representación espectral a una representación de puntos de malla. La «resolución» del modelo (máximo número de ondas) determina la separación y la posición exacta de los puntos de malla. La posición y la separación de los puntos se deciden para que coincida en la mayor medida posible con la resolución espectral del modelo (máximo número de ondas) y permita calcular de la forma más exacta los términos dinámicos no lineales. Sin embargo, debido a que la física del modelo también se calcula en esta malla, pueden surgir problemas cuando los efectos locales de la física introducen errores durante la transformación de los valores de malla de vuelta a una representación espectral.
Esta ilustración muestra el proceso de realizar los cálculos en una malla para un modelo espectral.
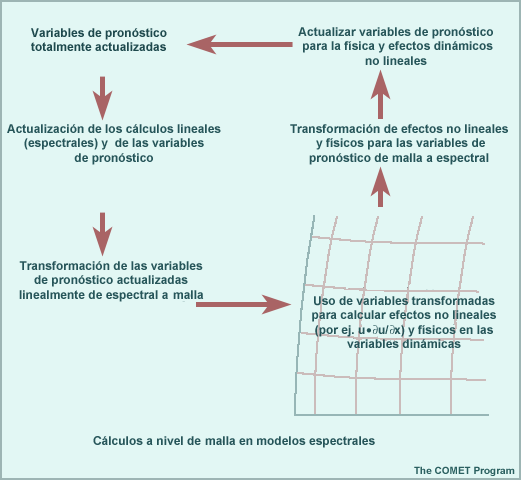
Los siguientes son algunos de los impactos específicos producto de realizar los cálculos de física en una malla:
- Los cálculos sobre malla están sujetos a las limitaciones normales de los modelos de malla, por ejemplo, los errores en el cálculo de estimación de los gradientes.
- Los errores en los términos de tendencia temporal de las variables de pronóstico se trasladan al espacio espectral, lo cual significa que estos errores no se eliminan.
- Debido a que los procesos físicos a menudo no producen tendencias temporales ondulatorias para las variables de pronóstico, se producen distorsiones al convertir las estructuras escalonadas en ondas. Un ejemplo muy claro es la tendencia temporal de la temperatura debido al calor latente liberado en el proceso de precipitación. En el borde externo de una región de precipitación estos campos tienden a ser más 'escalonados' que 'ondulatorios'. Cuando el escalón en la tendencia temporal de liberación del calor latente entre puntos de malla se transforma en una representación espectral, la distorsión se propaga a través del dominio del modelo (aunque su amplitud disminuye con la distancia del escalón). Los modelos espectrales utilizan métodos de filtrado para minimizar los efectos de estas distorsiones en las variables de pronóstico. Además, el posprocesamiento de los datos incluye filtros para reducir el ruido en los campos físicos.
- Los patrones producidos por los procesos físicos que ocurren en varios puntos de malla adyacentes pueden causar oscilaciones menores en la representación espectral de las longitudes de onda más cortas. Aunque el efecto total es del orden de un porcentaje pequeño, se puede extender a grandes distancias a ambos lados de la fuente de forzamiento físico. Por lo tanto, el calentamiento provocado por una intensa liberación de calor latente hace que la dinámica del modelo responda a pequeñas cantidades de calor en lugares donde físicamente no hay. Como las oscilaciones son del orden de un porcentaje pequeño, el efecto en un momento dado es mínimo. Sin embargo, debido a que esto ocurre constantemente en diferentes lugares del modelo, el resultado es un ruido de fondo espurio de pequeña escala superpuesto a la parte confiable del pronóstico. Este efecto también se puede ver en la elevación del terreno del modelo GFS (vea la sección «Resolución horizontal»).
Modelos no hidrostáticos
En el pasado, todos los modelos numéricos eran hidrostáticos, lo cual significa que la ecuación de movimiento vertical se simplifica para producir el balance supuesto entre el peso de la atmósfera y el gradiente de presión vertical. El movimiento vertical no se calcula directamente, sino se diagnostica a partir de otras variables pronosticadas. Esta simplificación, que casi no tiene efecto alguno en la predicción de los fenómenos de gran escala, permitía ejecutar el modelo más rápidamente.
Con la evolución hacia modelos de resolución más alta, se han introducido modelos numéricos no hidrostáticos. En 2006, los Centros Nacionales de Predicción Ambiental (National Centers for Environmental Prediction, NCEP) de EE.UU. suplantaron el modelo hidrostático Eta por el modelo de mesoescala no hidrostático, y varios otros centros han implementado modelos operativos de este tipo. Los modelos no hidrostáticos resuelven la ecuación de movimiento vertical completa para dar una solución directa del movimiento vertical. Aunque este cálculo aumenta la cantidad de tiempo necesaria para ejecutar el modelo, esto es necesario para obtener la respuesta correcta cuando la magnitud de las aceleraciones verticales es grande en comparación con las aceleraciones horizontales, como ocurre en las células convectivas profundas.
¿Qué toman en cuenta los modelos no hidrostáticos?
| Hidrostático | No hidrostático | |
|---|---|---|
| Empuje hidrostático: | Indirectamente (se crean primero los gradientes de presión horizontal, después la convergencia y finalmente el movimiento vertical) | Directamente (empuje hidrostático - movimiento vertical) |
| Efecto de la presión de la perturbación contra el empuje hidrostático | No | Sí, es importante para regular la velocidad de las corrientes convectivas ascendentes y la estructura de la nube convectiva, así como para propagar la energía de las ondas de gravedad |
| Movimiento vertical previo | No | Sí, el movimiento vertical se propaga |
| Acumulación de agua | No | Sí |
¿Cuándo es suficiente un modelo hidrostático?
En comparación con otros términos, los términos no hidrostáticos cambian a escala en proporción con la aceleración vertical dividida por la gravedad
(1/g) dw/dt
donde w es el movimiento vertical y g es la aceleración de la gravedad. Esta es una cantidad pequeña, incluso en las corrientes ascendentes de una tormenta violenta, pero el efecto general tiene repercusiones más grandes. La aproximación hidrostática solo funciona bien con fenómenos cuya longitud horizontal (L) es mayor que su profundidad vertical (P):
L >> P
| Modelo hidrostático suficiente, casi no hay diferencia |
Se precisa un modelo no hidrostático |
|---|---|
| Circulación de brisa marina | Vórtices horizontales de la capa límite planetaria |
| Ondas de montaña largas y suaves | Ondas de montaña empinadas |
| Circulación radial media de un huracán | Pared del ojo de un huracán |
| Vórtice de CCM y patrón inclinado medio de ascenso de atrás hacia adelante y descenso de adelante hacia atrás | Elementos convectivos de CCM |
| Forzamiento diabático entre débil y moderado | Calentamiento por liberación de calor latente muy intenso y concentrado |
| Circulación frontal | Cuerda o banda de nubes junto a un frente |
| Microfísica no muy acoplada a la dinámica, evolución | La retroalimentación de microfísica es importante |
| Existencia de una onda de gravedad | Predicción de propagación y conducción de ondas de gravedad |
Resolución y representación de estructuras
Los modelos que se ejecutan con una distancia de pocos km o menos entre puntos de malla tienen que ser no hidrostáticos. Típicamente, estos modelos de alta resolución pronostican estructuras de mesoescala detalladas y los impactos de pronóstico asociados para las áreas circundantes. Por ejemplo, el pronóstico de un sistema convectivo de mesoescala incluirá un frente de turbonada bien definido, el efecto de un yunque denso en la temperatura superficial corriente abajo y los efectos de la mesoalta a la zaga del sistema sobre los vientos a cierta distancia de la zona de convección activa. Aunque estos detalles se verán similares a los tipos de estructuras que se observan en los sistemas convectivos reales, el pronóstico del inicio de la convección estará sujeto a un error considerable que puede afectar de forma negativa todo el pronóstico. Por lo general, los detalles a nivel de mesoescala se pronostican de forma más confiable cuando son el producto de la topografía o las líneas costeras. En otras situaciones, si bien la estructura detallada puede darnos una idea de lo que podemos anticipar si se produce el evento meteorológico que la ocasiona, el pronóstico de la posición y el momento de desarrollo del evento puede estar sujeto a un error considerable.
*Dinámica de modelos no hidrostáticos
En la actualidad, la mayoría de los modelos no hidrostáticos utilizan formulaciones de puntos de malla. Por lo general se aplican a problemas de pronóstico que requieren una resolución horizontal muy alta (entre decenas de metros y unos pocos kilómetros) y abarcan dominios relativamente pequeños.
Los modelos no hidrostáticos pueden pronosticar de forma explícita el empuje hidrostático en la atmósfera y sus efectos detallados en la evolución de la convección profunda. Para lograrlo, los modelos no hidrostáticos deben incluir una ecuación de pronóstico adicional que considera las aceleraciones y los movimientos verticales directamente, en lugar de limitarse a diagnosticar el movimiento vertical a partir de la divergencia horizontal. La forma básica de la ecuación es similar a la de la ecuación de pronóstico del viento horizontal. Conceptualmente establece que:

Además de los cambios en el movimiento vertical debidos a los cambios en el ascenso y descenso orográfico, los cambios en el movimiento vertical de un intervalo de tiempo al siguiente en la celda son causados por:
- Advección que introduce aire cuya velocidad vertical es diferente.
- Desviaciones del balance hidrostático de la presión producto de:
- cambios en la convergencia/divergencia horizontal;
- fenómenos con perturbaciones no hidrostáticas de la presión, como tormentas y ondas de montaña.
- Empuje hidrostático (B): El empuje hidrostático positivo (negativo) genera
una tendencia al movimiento
ascendente (descendente). El empuje hidrostático positivo es producto de:
- anomalías positivas de temperatura en una celda de la malla con respecto a su alrededor;
- mayor contenido de humedad en una celda de la malla con respecto a su alrededor.
- Arrastre descendente causado por el peso de agua líquida o congelada en la nube y la precipitación.
Además, para representar adecuadamente los movimientos verticales y el empuje hidrostático las ecuaciones de pronóstico de temperatura y humedad de los modelos no hidrostáticos deben incluir una gran cantidad de detalles sobre los procesos de las nubes y de precipitación. Dado que los modelos hidrostáticos no incluyen una ecuación de pronóstico del movimiento vertical, ninguno de estos procesos puede afectar los movimientos verticales en sus predicciones.
La dinámica de los modelos no hidrostáticos difiere de manera fundamental de la de los modelos hidrostáticos. En una atmósfera hidrostática, los movimientos verticales se ajustan instantáneamente: cuando la temperatura cambia en altura, se percibe un cambio de presión en la superficie. En la atmósfera real, que no es hidrostática, el efecto de tales cambios de temperatura se propaga a una velocidad finita a través de la columna atmosférica. Los modelos no hidrostáticos reproducen este proceso de reajuste rápido en lugar de imponer un cambio instantáneo. Esto también afecta la interpretación científica de los flujos energéticos de las estructuras de escala más grande, incluso los ciclones sinópticos, aunque en la práctica sus efectos sobre el pronóstico son menores.
La propagación vertical de la energía de las ondas de gravedad es un proceso intrínsecamente no hidrostático. Esto puede afectar la predicción de los patrones tridimensionales de turbulencia en aire claro o las condiciones que se pueden diagnosticar como turbulencia en aire claro en proximidad de las montañas o alrededor de actividad convectiva. Además, afecta profundamente el proceso de ajuste dinámico que ocurre en respuesta a una zona de convección o delante del máximo de velocidad de una corriente en chorro con un fuerte gradiente de velocidad en la dirección del chorro. Tanto los modelos hidrostáticos como los no hidrostáticos generan una dorsal en altura arriba de la convección y una circulación vertical en la región de salida del chorro, pero el modelo hidrostático es incapaz de representar correctamente la transición hasta la evolución de dichos fenómenos y su eventual estructura también puede ser incorrecta.
Preguntas
Pregunta 1
Pregunta
¿Qué características de las ecuaciones de pronóstico del modelo limitan la exactitud del pronóstico? Escoja todas las opciones pertinentes.
Las respuestas correctas son (a) y (b).
Las ecuaciones son limitadas por las aproximaciones en los términos físicos y los métodos matemáticos usados para derivar las ecuaciones, que producen aproximaciones en las soluciones, incluso si los valores iniciales de los términos se determinan con exactitud. La exactitud de las soluciones de las ecuaciones de pronóstico del modelo afecta directamente la salida del modelo de pronóstico. Las ecuaciones se pueden resolver con exactitud, especialmente en los modelos de mayor resolución que utilizan métodos espectrales.
Pregunta 2
Pregunta
Escoja todas las opciones que completan el enunciado correctamente. El uso de métodos de malla o espectrales en los modelos numéricos permite... Escoja todas las opciones pertinentes.
Las respuestas correctas son (b) y (d).
Para realizar los cálculos de las ecuaciones del modelo, la representación de la atmósfera completa y el marco matemático deben ser finitos. Sin embargo, ambos métodos llevan a una representación incompleta de la atmósfera debido a las aproximaciones incorporadas en las ecuaciones del modelo y en los métodos utilizados para resolverlas. Por lo tanto, no es posible obtener soluciones de precisión absoluta y los cálculos en todas las formulaciones del pronóstico contienen errores.
Pregunta 3
Pregunta
Complete las siguientes afirmaciones relacionadas con el uso de cada tipo de modelo. Use el cuadro de selección para elegir la mejor respuesta para el enunciado.
Para contestar esta pregunta es preciso considerar cómo se representan los campos en cada tipo de modelo. Los modelos espectrales utilizan funciones de onda continuas, mientras que los modelos de malla utilizan celdas de malla discretas para definir los campos meteorológicos. La consecuencia de estas diferencias es que los modelos espectrales tienden a generar una mejor representación de los campos globales y los gradientes, mientras que los modelos de malla se prestan mejor a aplicaciones de área limitada y tienden a producir mejores representaciones de los efectos de los procesos físicos sobre la evolución del tiempo.
Pregunta 4
Pregunta
Complete las siguientes afirmaciones, las cuales definen las diferencias fundamentales entre los modelos hidrostáticos y no hidrostáticos. Use el cuadro de selección para elegir la mejor respuesta para el enunciado.
La diferencia fundamental entre los modelos hidrostáticos y no hidrostáticos es que los modelos no hidrostáticos pueden pronosticar explícitamente el movimiento vertical y no suponen el balance hidrostático, como en el caso de los modelos hidrostáticos.
Los modelos no hidrostáticos tienen un término adicional que incluye una ecuación de pronóstico para el movimiento vertical. Los modelos hidrostáticos no incluyen una ecuación de pronóstico para el movimiento vertical y, por tanto, no se pueden utilizar para simular células convectivas y otros fenómenos cuya profundidad se acerca a su anchura. Si los modelos hidrostáticos se ejecutan a una resolución muy alta (menos de 10 km), pueden tratar de simular eventos no hidrostáticos y generar errores grandes en el viento y campos de movimiento vertical espurios y exagerados. Por lo tanto, los modelos no hidrostáticos pueden ser útiles para pronosticar fenómenos de menor escala que no se pueden manipular con los modelos hidrostáticos.
Los modelos no hidrostáticos suelen aplicarse a problemas de pronóstico que requieren una resolución horizontal muy alta (desde decenas de metros hasta algunos kilómetros) y, por tanto, abarcan dominios relativamente pequeños. Los cálculos no hidrostáticos son costosos y brindan poca ventaja en cuanto a exactitud, excepto a escalas muy pequeñas. Como resultado, por lo general los modelos que pronostican fenómenos globales de escala sinóptica han sido hidrostáticos, pero en tiempos recientes se ha visto una marcada tendencia hacia el uso de modelos numéricos operativos con resoluciones altas sobre dominios grandes.
Pregunta 5
Pregunta
¿Qué tipo de modelo es mejor para pronosticar cada fenómeno? Use el cuadro de selección para elegir la mejor respuesta para el enunciado.
Los modelos espectrales son mejores para pronosticar los patrones de ondas planetarias para los próximos siete días y la cantidad de precipitación total para los siguientes 5 días en la costa oeste de Norteamérica. Esto se debe a que las formulaciones espectrales permiten la integración en tiempo real de las ecuaciones primitivas sobre un intervalo de tiempo mayor que los modelos de malla. Es más, los dominios globales de los modelos espectrales son mejores para representar características de escala planetaria, mientras que los modelos de malla a menudo tienen fronteras definidas donde pueden producirse errores debido a inexactitud e incoherencia en las condiciones de frontera. Un modelo de malla global también podría ser una buena opción, aunque no se ofreció como posible respuesta.
Los modelos de malla hidrostáticos pueden pronosticar mejor los fenómenos sinópticos y subsinópticos que no se ven afectados fuertemente por el empuje hidrostático, como la precipitación orográfica, los vientos de la capa límite y la intensidad y ubicación de chorros. Debido a su mayor resolución y a la representación más detallada de las características topográficas, los modelos de malla suelen describir mejor la precipitación cerca del suelo.
Los modelos de malla no hidrostáticos pueden pronosticar mejor el desarrollo y la evolución de los sistemas convectivos de mesoescala y la propagación de fronteras de flujo saliente. Sólo los modelos no hidrostáticos pueden pronosticar explícitamente la convección profunda, dado que toman en cuenta las aceleraciones verticales debidas al empuje hidrostático. En los modelos hidrostáticos solo se puede parametrizar la convección y no se pueden representar los procesos termodinámicos que se producen dentro de la convección profunda. Los modelos no hidrostáticos son también necesarios para modelar el flujo en escalas menores de 10 km.
Resumen
MODELOS DE MALLA
Características
- Los datos se representan en un conjunto fijo de puntos de malla.
- La resolución es función del espaciamiento de los puntos de malla.
- Todos los cálculos se realizan en los puntos de malla.
- Se utilizan aproximaciones de diferencias finitas para resolver las derivadas de las ecuaciones del modelo.
- Se introduce un error a través de las aproximaciones por diferencias finitas de las ecuaciones primitivas.
- El grado de error es función del espaciamiento de la malla y del intervalo de tiempo.
Desventajas
- Las aproximaciones por diferencias finitas de las ecuaciones del modelo introducen un error considerable.
- Se acumula ruido de pequeña escala cuando se integran las ecuaciones por períodos largos.
- La magnitud de los errores de cómputo suele ser mayor que en los modelos espectrales de resolución comparable.
- Los errores en las condiciones de frontera se pueden propagar a los modelos regionales y pueden afectar la habilidad del pronóstico.
Ventajas
- Pueden proporcionar una alta resolución horizontal en aplicaciones regionales y de mesoescala.
- No necesitan transformar los cálculos físicos desde y hacia el espacio de malla.
- A medida que la física en los modelos operativos se vuelve más compleja, los modelos de malla se vuelven más competitivos con los modelos espectrales desde el punto de vista computacional.
- Las versiones no hidrostáticas pueden pronosticar explícitamente los detalles de convección, dada una resolución adecuada y suficiente detalle en las condiciones iniciales.
MODELOS ESPECTRALES
Características
- Los datos se representan mediante funciones de onda.
- La resolución es una función del número de ondas utilizado en el modelo.
- La resolución del modelo está limitada por el número máximo de ondas.
- Las cantidades lineales de las ecuaciones de movimiento se pueden calcular sin introducir errores de cómputo.
- Se utiliza una malla para ejecutar cálculos físicos y no lineales.
- Se producen transformaciones entre el espacio espectral y de malla.
- Las ecuaciones se pueden integrar para pasos de tiempo y períodos largos.
- Se diseñaron originalmente para dominios globales.
Desventajas
- Las transformaciones entre cálculos de física espectrales y de malla introducen errores en la solución del modelo.
- En términos generales, no han sido diseñados para aplicaciones regionales y de mesoescala de alta resolución.
- El ahorro en recursos de cómputo disminuye conforme aumenta el grado de realismo físico del modelo.
Ventajas
- La magnitud de los errores de cómputo en los cálculos de dinámica suele ser menor que en los modelos de malla con una resolución comparable.
- Pueden calcular las cantidades lineales de las ecuaciones de movimiento con exactitud.
- A la resolución horizontal que típicamente es necesaria para un modelo global requieren menos recursos de cómputo que un modelo de malla con una resolución horizontal y procesos físicos equivalentes.
MODELOS HIDROSTÁTICOS
Características
- Utilizan las ecuaciones primitivas hidrostáticas, diagnostican el movimiento vertical a partir de movimientos horizontales previstos.
- Se utilizan para pronosticar fenómenos de escala sinóptica, pueden pronosticar algunos fenómenos de mesoescala.
- Se emplean en modelos de malla y espectrales.
Desventajas
- No son capaces de predecir las aceleraciones verticales.
- No pueden predecir los detalles de los procesos de mesoescala asociados con el empuje hidrostático.
Ventajas
- Pueden ejecutarse rápidamente sobre dominios de área limitada y brindar pronósticos a tiempo para usos operativos.
- El supuesto hidrostático es válido para muchos fenómenos de escala sinóptica y subsinóptica.
MODELOS NO HIDROSTÁTICOS
Características
- Utilizan las ecuaciones primitivas no hidrostáticas, pronostican el movimiento vertical en forma directa.
- Se utilizan para pronosticar fenómenos de escala pequeña.
- Pueden predecir estructuras de mesoescala detalladas y realistas, así como el impacto en las condiciones meteorológicas en la zona, lo cual produce pronósticos locales de calidad superior (a veces) o errores grandes (otras veces).
Desventajas
- Tardan más tiempo en ejecutarse que los modelos hidrostáticos de resolución y dominio iguales.
- Se utilizan en aplicaciones de área limitada, de modo que necesitan condiciones de fronteras de otro modelo; si las condiciones de frontera no cuentan con la estructura y resolución características de los campos que evolucionan dentro del dominio del modelo, pueden producir efectos adversos en el pronóstico.
- Pueden predecir fenómenos con un aspecto realista, pero el momento y la posición pueden ser poco confiables.
Ventajas
- Calculan el movimiento vertical de forma explícita.
- Predicen explícitamente la liberación de empuje hidrostático.
- Tienen en cuenta los procesos de nubes y precipitación y su aporte a los movimientos verticales.
- Son capaces de predecir la convección y las ondas orográficas.
Coordenadas verticales
Introducción
Introducción
Al igual que la configuración horizontal y el tipo de modelo, la estructura vertical es fundamental para establecer el comportamiento del modelo. Para poder representar apropiadamente la estructura vertical de la atmósfera es necesario seleccionar un sistema de coordenadas adecuado y una resolución vertical suficiente.
A diferencia de la estructura horizontal, cuya configuración puede ser discreta o continua (de malla o espectral), la estructura vertical de prácticamente todos los modelos operativos es discreta. Esto significa que los pronósticos que producen representan un promedio de una capa atmosférica entre las superficies de las coordenadas verticales, no en las superficies mismas.
Esta sección describe los diversos sistemas de coordenadas verticales que se utilizan en los modelos operativos.
*Criterios de selección de coordenadas
A la hora de escoger un sistema de coordenadas verticales para un modelo numérico, las coordenadas:
- Deben decrecer continuamente (por ejemplo: coordenadas de presión) o aumentar continuamente en la vertical (por ejemplo: coordenadas isoentrópicas). Es decir, la coordenada debe exhibir un comportamiento monotónico con la altura. Esto evita que las superficies de las coordenadas aparezcan en diversos niveles de la atmósfera.
- Deben mantener propiedades atmosféricas conservadoras y tratar con exactitud los procesos dinámicos importantes, como los movimientos diabáticos y adiabáticos y el flujo sobre el suelo.
- Deben representar con exactitud la fuerza del gradiente de presión (utilizada para calcular el viento geostrófico) sobre terreno plano o en declive.
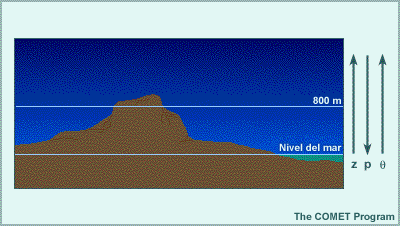
La mayoría de los modelos hidrostáticos utilizan configuraciones relativamente sencillas para sus coordenadas verticales. Sin embargo, ningún sistema de coordenadas verticales es perfecto, ya que cada uno tiene sus ventajas y limitaciones. Por ejemplo:
- El uso de coordenadas sigma, en lugar de presión o altura, evita las complicaciones que surgen cuando las superficies de presión o de altura intersecan el suelo, especialmente en zonas montañosas.
- En muchas circunstancias, el uso de coordenadas eta en lugar de coordenadas sigma mejora el cálculo de los vientos y el movimiento vertical en áreas con pendiente pronunciada.
- El uso de coordenadas isoentrópicas mejora los pronósticos en procesos de escala fina cerca de frentes y corrientes en chorro, pero introduce dificultades cerca de la superficie terrestre.
La elección de las coordenadas verticales para los modelos no hidrostáticos implica restricciones adicionales que se deben considerar.
Coordenadas sigma
Coordenada sigma
La expresión más simple de las ecuaciones de movimiento, las cuales constituyen la base de todos los modelos de predicción numérica del tiempo, se obtiene en las coordenadas de presión. Desafortunadamente, los sistemas de coordenadas de presión no son los más apropiados para resolver las ecuaciones de pronóstico porque, al igual que las superficies de igual altura, pueden intersecar montañas y por consecuencia «desaparecer» en determinadas partes del dominio de predicción. Para resolver el problema de la discontinuidad de las superficies en el área del pronóstico, Phillips (1957) desarrolló la coordenada sigma (σ), ilustrada abajo, que sigue el contorno del terreno. Aunque tradicionalmente la coordenada sigma se ha usado en la mayoría de los modelos de PNT, en tiempos recientes muchos modelos han adoptado sistemas híbridos en los cuales se emplea una coordenada sigma que sigue el contorno del terreno en los niveles bajos y se transforma en algún otro sistema de coordenadas en altura.
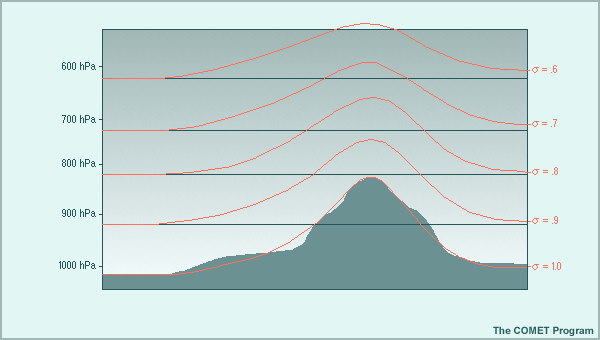
En su forma más simple, el sistema de coordenadas sigma se define por σ = p/ps, donde p es la presión en un nivel de pronóstico dentro del modelo y ps es la presión en la superficie terrestre (no la presión al nivel medio del mar). La superficie de coordenadas más baja (que suele rotularse σ = 1) sigue una versión suavizada del terreno. Cabe notar que las pendientes del terreno utilizadas en los modelos sigma siempre se suavizan en alguna medida. Las otras superficies sigma pasan gradualmente de ser prácticamente paralelas al terreno suavizado en el nivel inferior del modelo (σ = 1) a ser casi horizontales respecto a las superficies de presión constante en el nivel superior del modelo (σ = 0). Por lo general, el nivel superior del modelo se sitúa considerablemente más allá de la tropopausa, normalmente entre 25 y 1 hPa.
Las coordenadas verticales sigma también se pueden formular con respecto a la altura (z), en lugar de la presión. A pesar de que en la actualidad esta modalidad no se utiliza en los modelos operativos, sí se utiliza en el modelo RAMS. Para más información sobre la coordenada sigma-z, consulte Pielke y Martin, 1981.
Ventajas de la coordenada sigma
A continuación presentamos cuatro ventajas de la coordenada sigma. En algunos casos, necesitará contestar una pregunta.
Ventaja 1: Debido a que la coordenada sigma está relacionada con la presión, genera formulaciones relativamente simples para manejar el límite inferior sin complicar excesivamente las ecuaciones de movimiento. Las formulaciones simplificadas son más fáciles de programar.
Ventaja 2: La coordenada sigma se ajusta a terrenos con pendiente.
Pregunta
¿Qué tipos de fenómenos nos permite pronosticar esta característica de los modelos que utilizan coordenadas sigma? Escriba su respuesta en el espacio siguiente.
Comentario
La capacidad de las coordenadas sigma de seguir la forma del terreno permite representar bien los campos continuos, como la advección de temperatura y vientos, especialmente en las áreas donde el terreno varía mucho, pero de manera uniforme. Además, la coordenada sigma puede pronosticar fenómenos tales como los vientos catabáticos a sotavento de las montañas. Sin embargo, dado que este sistema de coordenadas permite el flujo continuo sobre las montañas, puede tener dificultades para pronosticar situaciones en las que las montañas actúan como barreras, como ocurre con los casos de estancamiento o empozamiento de aire frío y la ciclogénesis a sotavento de las montañas.
Ventaja 3: La capacidad de las coordenadas sigma de seguir la forma del terreno se presta para incrementar la resolución vertical cerca del suelo de forma coherente en todo el dominio del modelo.
Pregunta
¿Cuál es la ventaja de una mayor resolución en la baja atmósfera? Escriba su respuesta en el espacio siguiente.
Comentario
La ventaja consiste en que el modelo puede pronosticar mejor los procesos y las características de la capa límite que contribuyen considerablemente a los elementos meteorológicos sensibles, tales como calentamiento diurno, vientos en los niveles inferiores, turbulencia, humedad en los niveles inferiores y estabilidad estática.
Ventaja 4: A diferencia de las coordenadas de presión, de altura e isoentrópicas, la coordenada sigma elimina el problema de la intersección del suelo por las superficies de las coordenadas verticales. Los otros sistemas de coordenadas pueden intersecar la superficie terrestre en áreas de terreno irregular o en áreas con fuertes variaciones de la presión superficial debido a sistemas atmosféricos.
Pregunta
Desde el punto de vista meteorológico, ¿por qué es un problema que las superficies verticales de un modelo intersequen al suelo? Escriba su respuesta en el espacio siguiente.
Comentario
Cuando una capa del modelo interseca el suelo, el campo de viento (y, por tanto, la advección de temperatura y humedad) en el área puede verse interrumpido o bloqueado, lo cual es físicamente incorrecto. Para compensar este error, es necesario usar técnicas matemáticas sofisticadas en el modelo.
Limitaciones de la coordenada sigma
Limitación 1: Los pronósticos de viento del modelo dependen del cálculo exacto de la fuerza del gradiente de presión, que es muy simple de calcular en coordenadas de presión cuando se conoce la altura. Sin embargo, cuando las superficies sigma se inclinan, la fuerza del gradiente de presión se debe ampliar para incluir los efectos de la pendiente de su forma simple en coordenadas de presión. Esto introduce errores, porque es preciso aproximar el gradiente vertical de temperatura para los puntos localizados entre las superficies de presión para las cuales se cuenta con observaciones de altura. Este error puede volverse muy grande en zonas de montaña con laderas muy empinadas. Debido a que las ecuaciones de pronóstico del viento dependen de la fuerza del gradiente de presión, esto puede causar un error considerable en el pronóstico del viento y afectar al modelo en todos los niveles, especialmente en situaciones donde el flujo descendente por las laderas y el gradiente de presión son grandes.
Limitación 2: Debido a que las pendientes reales de las montañas, que con frecuencia son muy empinadas, se suavizan en los modelos de coordenadas sigma, a menudo estos modelos representan incorrectamente la verdadera elevación de la superficie. Esto puede causar la representación muy incorrecta de la presión en la superficie y, por tanto, de la temperatura y humedad, en los pronósticos de los lugares contiguos a las montañas. Por ejemplo, como los modelos sigma suavizan el terreno, un modelo sigma de 80 km puede localizar la elevación de las estaciones contiguas a las montañas, como Denver, en Colorado, hasta 500 m por encima de la realidad. Esto puede producir errores de hasta 5 °C en la temperatura en la superficie por la tarde.
Limitación 3: Debido al suavizado necesario en las cadenas de montañas a lo largo de las costas oceánicas, en el modelo los puntos en tierra firme pueden verse forzados a extenderse más allá de la verdadera línea costera. En el caso de las costas de Estados Unidos y Canadá en el noroeste del Pacífico, debido al desplazamiento de la línea costera hacia el oeste en el modelo respecto de su posición real, las estaciones en esas zonas parecen estar localizadas más hacia el interior de los que es el caso en la realidad.
Limitación 4: Los modelos sigma pueden tener dificultades con las situaciones atmosféricas a sotavento de una montaña, por ejemplo, el empozamiento de aire frío y la ciclogénesis. En eventos de fuerte empozamiento de aire frío, la inversión (gradiente vertical de temperatura) sobre la masa de aire frío en la atmósfera real, que se muestra en el lado derecho de la figura, se transforma en parte en un gradiente de temperatura «horizontal» a lo largo de las superficies sigma muy empinadas. Como resultado, el modelo puede alejar el aire frío de las montañas por advección «horizontal» a lo largo de las superficies sigma, en lugar canalizar el flujo sobre las montañas y en sentido paralelo a la inversión, por encima del aire frío. De manera similar, un flujo descendiente excesivo en los niveles bajos puede resultar en un «estiramiento del tubo de vórtice» exagerado y en una ciclogénesis excesiva y demasiado frecuente a sotavento.
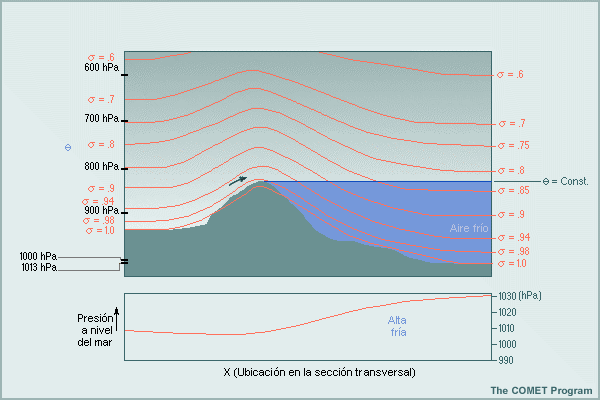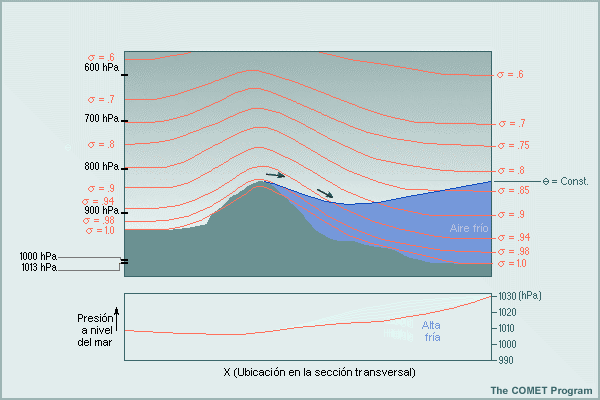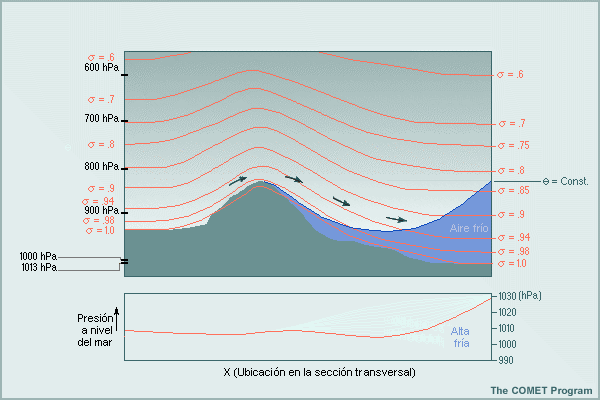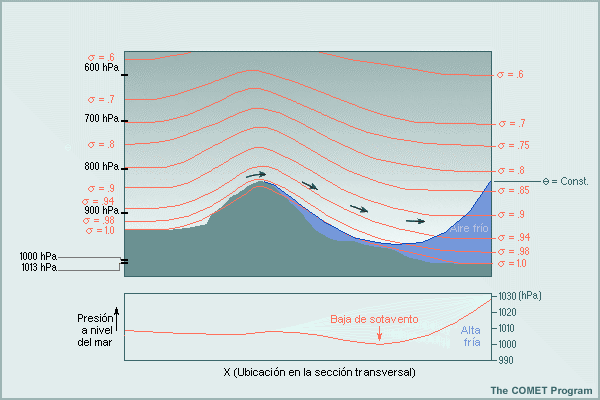
*Viento geostrófico y las coordenadas sigma
Veamos un ejemplo del cálculo de los cambios en el viento este-oeste en las columnas resaltadas en morado y verde en la ilustración siguiente. Para hacerlo, en primer lugar tenemos que calcular el viento geostrófico. En coordenadas de presión, la fuerza del gradiente de presión se calcula utilizando las alturas z1 y z2, lo cual considera directamente el cambio de altura de la superficie de presión en la dirección x. Este cambio representa el verdadero gradiente de presión este-oeste al que está sometido el aire dentro de esta celda de la malla, independientemente del sistema de coordenadas verticales que se utilice.

Para calcular la fuerza del gradiente de presión en un modelo sigma, debemos determinar un equivalente de z1 y z2 en la superficie de presión. Sin embargo, debido a que el modelo sigma solo produce datos a lo largo de las superficies de coordenadas sigma, tiene valores correspondientes en z3 y z4. Para convertir las alturas en la superficie sigma a las alturas correspondientes en la superficie de presión se requieren los dos términos adicionales indicados en la figura, pero esto introduce errores. Para determinar la diferencia de altura en la superficie sigma correspondiente a z2 - z1 es preciso calcular la diferencia entre la diferencia de altura a lo largo de la superficie sigma (z4 - z3) y el término de corrección (z2 - z4) + (z3 - z1), ambas partes del cual dependen del gradiente vertical de temperatura aproximado entre las superficies sigma. Estos dos términos son mucho mayores que la diferencia de altura en la superficie de presión, y la diferencia resultante en los términos puede producir errores significativos. Cuanto mayor la inclinación de la superficie sigma, como en el área verde, tanto mayor la posibilidad de error en la fuerza del gradiente de presión.
Información adicional: Cálculo de la fuerza del gradiente de presión en coordenadas sigma
El cálculo de la fuerza del gradiente de presión en coordenadas sigma está sujeto a error incluso cuando la topografía es moderada y el error se agudiza en terrenos con pendientes muy marcadas. La causa del error es el hecho de que el gradiente de presión horizontal en una superficie sigma inclinada está dominado por el gradiente de presión vertical hidrostático y se calcula como la diferencia de dos términos de gran magnitud.
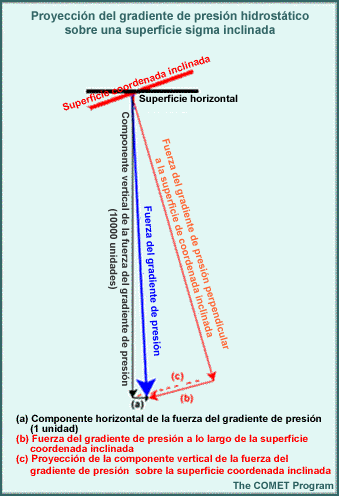
La componente horizontal de la fuerza del gradiente de presión, que es obligatoria en las ecuaciones de pronóstico del viento, es pequeña en comparación con la componente vertical. La relación entre estas componentes se encuentra a partir de la relación entre el viento geostrófico y la ecuación hidrostática, y viene siendo f Vg/g, donde:
- f es el parámetro de Coriolis, aproximadamente 10-4 s-1 en latitudes medias
- Vg es la velocidad del viento geostrófico
- g es la aceleración de la gravedad, 9,8 m/s-2
Para un viento geostrófico de aproximadamente 10 m/s, este cociente es del orden de 10-4. El gradiente de presión vertical es 10000 veces mayor que el gradiente de presión horizontal. Por eso incluso un error pequeño en la pendiente orográfica puede introducir un error considerable en el gradiente de presión y, por lo tanto, en el pronóstico del viento.
Procediendo de otro modo, el mismo vector fuerza del gradiente de presión se puede descomponer en una componente perpendicular a la coordenada sigma inclinada y otra a lo largo de la superficie sigma, como se ilustra en la figura. En este ejemplo, coherente con la situación de la columna en morado de la figura anterior, la presión es mayor a la derecha. Sin embargo, debido a que la superficie de las coordenadas está inclinada y sube rápidamente hacia la derecha, la presión en la superficie de las coordenadas, indicada por el vector (b), es mucho mayor a la izquierda. Para obtener el valor (a) necesario para la ecuación de pronóstico de viento, es preciso restar la porción (c) del vector fuerza del gradiente de presión vertical, que se proyecta sobre la superficie de coordenadas inclinada. Este es el término de corrección.
La magnitud del vector (c) en este ejemplo es la pendiente de la superficie sigma multiplicada por 10000 unidades. En las Grandes Planicies de los Estados Unidos, la pendiente oscila entre 0,001 y 0,002, por lo que (c) es de 10 a 20 veces más grande que (a) cerca del suelo y la mitad de eso en la troposfera media. Esto significa que un error del 1 % en las variables de pronóstico utilizadas para determinar (b) y (c) puede redundar en un error mayor al 10 % en el gradiente de presión utilizado para pronosticar el viento horizontal. Sobre terrenos montañosos, las consecuencias son mucho más graves. El efecto en el viento pronosticado es aún peor de lo que parece a primera vista, porque los cambios en el viento se deben al desequilibrio entre el viento geostrófico y el gradiente de presión horizontal. Si el viento ageostrófico es un 10 % mayor que el viento geostrófico, un error del 10 % en el cálculo del gradiente de presión horizontal produce un error del 100 % en los cambios pronosticados para el viento horizontal. Aunque se utilizan varias técnicas numéricas para realizar los cálculos con la mayor exactitud posible, todas tienen limitaciones.
Además, si solo se utiliza sigma como coordenada vertical en un terreno inclinado, la deformación de las superficies que siguen el contorno del terreno y las dificultades asociadas con el cálculo del gradiente de presión horizontal se extienden más allá de la topografía del modelo.
*Coordenadas eta
*Coordenada eta
La coordenada Eta se utilizó en el modelo de mesoescala principal de NCEP entre 1993 y 2006 y en 10 de los 21 miembros del conjunto NCEP a corto plazo hasta 2009, cuando se redujeron a 6 con miras a eliminarlos por completo en el futuro. En el año 2009 sigue utilizándose en modelos regionales ejecutados por organizaciones de pronóstico públicas y privadas en varios países de Europa, América Central y América del Sur, pero no en Canadá, Europa Occidental y Japón. En algunos casos se ha evolucionado de la coordenada escalonada tradicional que describimos al comienzo de la explicación que sigue, a otra que emplea «pasos suavizados», que se describe más adelante.
La coordenada vertical eta (η) fue creada a principios de los años 80 para tratar de reducir los errores en el cálculo de la fuerza del gradiente de presión en los modelos que empleaban la coordenada sigma.
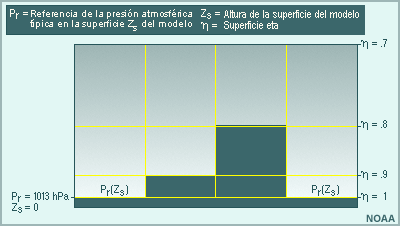
La coordenada eta es, de hecho, una forma de la coordenada sigma que utiliza la presión a nivel del mar en lugar de la presión superficial como nivel de referencia inferior. Por lo tanto, eta se define como:
ηs = (pr(zs) – pt )/ (pr(z=0)- pt)
Donde:
- pt es la presión en la parte superior del modelo;
- pr(z=0) es la presión atmosférica típica a nivel del mar (1013 hPa);
- pr(zs) es la presión atmosférica típica al nivel de superficie zs del modelo.
Normalmente, los niveles eta se identifican de 0 (la parte superior del dominio del modelo) a 1 (nivel del mar). A diferencia de los modelos sigma, en los que se considera que todas las celdas de la malla están encima de la superficie de la Tierra, en los modelos eta en las áreas donde la elevación de la superficie está notablemente por encima del nivel del mar, algunas de las celdas de la malla se encuentran debajo del suelo. Esto obliga a usar formulaciones numéricas especiales para modelar el flujo cerca de la superficie terrestre.
La diferencia en la definición de los sistemas de coordenadas sigma y eta permite representar la capa atmosférica inferior del modelo dentro de cada celda de la malla como un «escalón» plano, sin la inclinación que produce la coordenada sigma en terreno inclinado. Por esta razón, la coordenada eta se puede denominar también coordenada de montaña escalonada. Gracias a esta configuración, que elimina casi todos los errores en el cálculo de la fuerza del gradiente de presión, los modelos que utilizan la coordenada eta pueden manejar diferencias muy pronunciadas en elevación entre puntos de malla vecinos. Por lo tanto, los modelos de coordenada eta pueden desarrollar fuertes movimientos verticales en áreas de terreno empinado y representar con mayor exactitud muchos de los efectos de bloqueo que las montañas pueden ejercer sobre las masas de aire estable.
Aun usando el modelo escalonado eta como coordenada vertical, el terreno representado por el modelo es mucho más tosco que la topografía real, pero los gradientes topográficos se suavizan menos que en los modelos sigma. Aunque esta representación del terreno es una fuente de error en aquellas áreas que se ven fuertemente afectadas por características topográficas de pequeña escala, sigue siendo necesario representar una elevación promedio dentro de cada celda de la malla. Esta manera de representar el terreno influye en la escala de las características que se pueden conservar en los pronósticos del modelo, de modo que los pronósticos sean representativos de las condiciones promedio en la celda (encontrará más información en la sección Resolución horizontal Resolución horizontal).
*Cálculo de las superficies eta
Examinemos en detalle un ejemplo de cómo se determina el nivel eta más cercano a una estación meteorológica. Para fines de simplicidad, asignaremos 1000 hPa a la presión de referencia a nivel del mar.
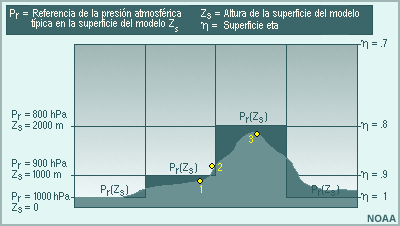
En primer lugar se deben definir las alturas de cada nivel del modelo. Para este ejemplo hemos definido un modelo eta de 10 capas (de las cuales solo se muestran tres) distribuidas de manera uniforme en términos de presión entre el nivel del mar y el límite superior de la atmósfera. A continuación se determina la presión atmosférica típica para cada una de estas alturas.
En el punto 1, la elevación real del terreno es de 848 m, lo cual representa la altura más cercana a la altura de 1000 m definida para el primer nivel eta. La presión atmosférica típica a esa altura es 900 hPa. ¿Cuál es entonces el nivel eta más cercano a este punto?
Utilizando la ecuación de eta ηs = (pr(zs) – pt )/ (pr(z=0)- pt)
η = (900-0) / (1000-0) = 0,9.
Si pasamos al punto 2, la altura real del terreno es 1126 m, y en este caso también la altura más cercana es 1000 m. Por lo tanto, el nivel eta más cercano a este punto también es 0,9.
Sin embargo, si consideramos al punto 3 (1832 m), la superficie eta más cercana en el modelo es 2000 m. Aquí, la presión atmosférica estándar es 800 hPa. Por lo tanto, el nivel eta más cercano es
η = 1 x (800-0 / 1000-0) = 0,8
Cabe observar que los niveles eta están predefinidos y la topografía del modelo se ajusta a la superficie eta más cercana, incluso si no coincide perfectamente con la altura promedio o suavizada del terreno en la celda de la malla.
Este es un ejemplo simplificado. En la realidad, los intervalos entre los niveles eta se deben escoger de manera tal de describir la capa límite planetaria (CLP) con suficiente detalle y, a la vez, representar los cambios promedio en la elevación sobre el dominio de pronóstico completo.
*Ventajas de la coordenada eta
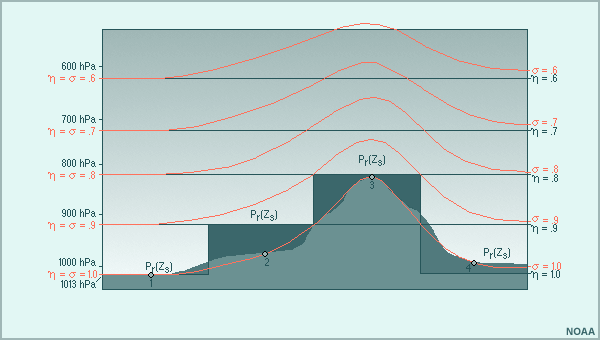
El hecho que la coordenada eta es casi horizontal y permite representar las características topográficas, como las montañas, en términos de bloques de tierra sólidos en diferentes niveles del modelo brinda varias ventajas importantes.
Ventaja 1: Los modelos eta no necesitan hacer las interpolaciones verticales que se requieren en los modelos sigma para calcular la fuerza del gradiente de presión (Mesinger y Janjic 1985). Esto reduce el error en el cálculo de la fuerza del gradiente de presión y mejora el pronóstico de los cambios en el viento, la temperatura y la humedad en áreas de terreno muy empinado.
Ventaja 2: Aunque la formulación numérica cerca de la superficie es más compleja, la convergencia de bajo nivel en áreas de terreno empinado es mucho más representativa de las condiciones atmosféricas reales de lo que es el caso en con las formulaciones más simples de los modelos sigma (Black 1994). Un mejor pronóstico de la convergencia de bajo nivel redunda en mejores pronósticos de precipitación en estas áreas. La mejora en el detalle predictible del flujo en comparación con los modelos sigma compensa sobradamente el poco tiempo de procesamiento adicional necesario.
Ventaja 3: En comparación con los modelos sigma, a menudo los modelos eta pueden mejorar los pronósticos de invasión de aire frío, eventos de empozamiento de aire frío y eventos de ciclogénesis a sotavento de las montañas (Mesinger y Black 1992, Mesinger et al. 1988). Por ejemplo, en eventos de empozamiento de aire frío, la inversión (gradiente de temperatura vertical) en la atmósfera real sobre la masa de aire frío que se muestra en la mitad derecha de la figura se conserva casi exactamente en un modelo eta. Como resultado, se genera poco o casi ningún gradiente de temperatura horizontal erróneo a sotavento de las montañas. Por lo tanto, el modelo canaliza el flujo sobre las montañas por encima y paralelo a la inversión de aire frío, en lugar de producir incorrectamente un flujo cuesta abajo. Mediante procesos similares el modelo eta puede conservar la integridad de las masas de aire frío y altas árticas que se desplazan hacia el sur a sotavento de las montañas. El mejoramiento de la descripción del flujo cuesta abajo también resulta en «estiramientos de tubos de vorticidad» más realistas (y, por lo tanto, en incrementos más exactos en la vorticidad) para los eventos de ciclogénesis a sotavento.
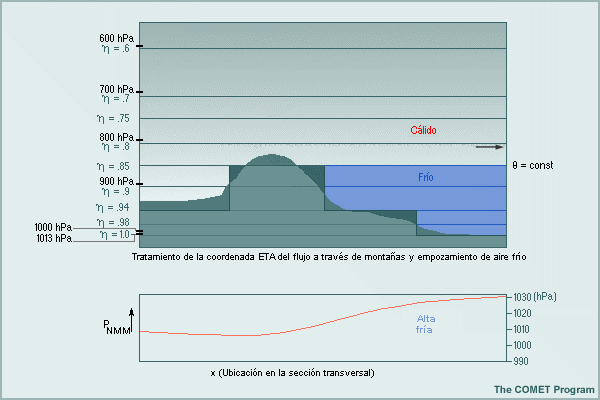
*Limitaciones de la coordenada eta
Si bien la coordenada eta brinda muchas ventajas útiles para el modelado numérico, también tiene algunas limitaciones.
Limitación 1: Debido a la naturaleza escalonada de la coordenada eta, es difícil retener la estructura vertical en la capa límite sobre todo el dominio del modelo, particularmente sobre terreno elevado.
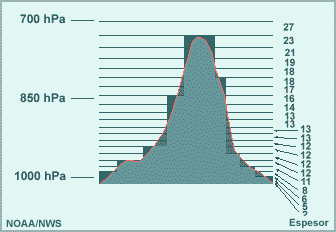
Debido a que normalmente la profundidad de las capas de un modelo eta aumenta con la elevación desde el nivel del mar, el sistema de coordenadas eta puede tener dificultades para representar los procesos de capa límite sobre terreno elevado. Por ejemplo, el espesor de la capa inferior del modelo sobre la cima de una montaña puede ser más de diez veces mayor que cerca del nivel del mar (2 hPa y 23 hPa, respectivamente). Esto contrasta con los modelos sigma, en los que la profundidad vertical de las capas inferiores es más uniforme a lo largo de todo el dominio del modelo. Este incremento en la profundidad de las capas del modelo cerca de la superficie puede afectar la capacidad del modelo de pronosticar procesos de superficie y de capa límite sobre terreno alto.
Además, dado que un número relativamente grande de las capas del modelo puede encontrarse bajo tierra, se dispone de menos capas para pronosticar los procesos atmosféricos sobre mesetas elevadas de altura uniforme.
Limitación 2: Los modelos eta no representan con exactitud los terrenos con pendiente gradual. Como toda la topografía se representa en pasos discretos, las zonas extensas con pendiente suave pueden quedar concentradas hasta en un solo paso. Esta compresión no realista de la pendiente en un área pequeña se puede compensar, en parte, incrementando la resolución vertical u horizontal.
Limitación 3: Los modelos eta tienen dificultades para predecir eventos extremos de vientos de ladera descendentes.
Staudenmaier y Mittelstadt (1997) documentaron los problemas de la coordenada eta para representar ondas de montaña a sotavento de barreras montañosas. Esto se debe a la tendencia del modelo eta de crear una separación del flujo sobre las pendientes escalonadas a sotavento del terreno del modelo. Sus resultados sugieren que este comportamiento puede haber provocado un pronóstico de flujo débil a sotavento de las montañas Wasatch durante un evento de viento catabático de gran intensidad.
Limitación 4: Los modelos eta deben ampliar los valles de algunas celdas de malla en extensión, o rellenarlos.
El modelo eta de NCEP configura el viento horizontal en cero en los lados de los escalones. Esto significa que un valle de dos espacios de malla de ancho tiene solo una fila de puntos de velocidad pronosticados, una cantidad insuficiente para calcular procesos divergentes.
Limitación 5: Las coordenadas eta pueden crear ondas falsas en los bordes de los escalones.
Estas ondas falsas pueden ser grandes e importantes solo si el modelo tiene una resolución horizontal considerablemente mayor a 10 km y si el aumento en la resolución vertical es una fracción considerable de la característica topográfica real (Gallus y Klemp 1999).
*Nuevos tipos de coordenadas eta
Las limitaciones 2, 3 y 5 que acabamos de describir se pueden eliminar utilizando una formulación de «pasos suavizados». En lugar de utilizar pasos completos para el terreno, la topografía del modelo se inclina para ajustarse a la topografía real en las esquinas de las celdas. Esto se ilustra de forma esquemática en la figura siguiente, que en lo demás es idéntica a la imagen que vimos en una sección anterior. Aunque los pasos inclinados siguen produciendo celdas gruesas, resolución vertical tosca y menos niveles verticales (porque algunos se encuentran bajo tierra) sobre terreno elevado, esta formulación reduce el bloqueo excesivo provocado por la topografía y elimina el tamaño arbitrario de los pasos al subir a terreno más alto. Es probable que el desarrollo futuro de modelos con coordenadas eta recurra a esta formulación u otra similar, en lugar de los pasos que llenan celdas completas.
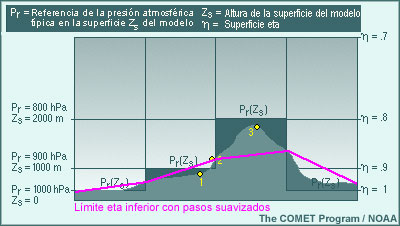
*Consideraciones sobre la coordenada eta
Pregunta
Supongamos que ha desarrollado e implementado un modelo local utilizando la coordenada vertical eta para reemplazar un modelo de coordenadas sigma. Su área de responsabilidad de pronóstico abarca dos ámbitos: una zona de planicie casi horizontal al oeste y una meseta muy alta al este. Usted quiere comunicar a los usuarios de su modelo dos aspectos esenciales. Use el cuadro de selección para elegir la mejor respuesta para el enunciado.
Los enunciados correctos son:
1. Tenga presente que la resolución de la capa límite no presentará tanto detalle sobre las montañas como sobre las planicies.
Recuerde que una de las desventajas de la coordenada eta es que las capas atmosféricas inferiores del modelo tienen menor resolución vertical en terreno muy elevado que a nivel del mar. Esto puede degradar la exactitud de los pronósticos de temperatura y estabilidad en los niveles bajos sobre terreno elevado. Sin embargo, este problema se puede aliviar agregando más superficies verticales para mantener la misma resolución en la cima de las montañas.
2. Debería observar un mayor grado de exactitud en el pronóstico del campo de viento de bajo nivel debido a que el cálculo del gradiente de presión horizontal sobre terreno inclinado es más exacto.
Dado que sobre terreno quebrado cada superficie eta es plana y no inclinada, como es el caso con la coordenada sigma, la coordenada eta produce un mejor pronóstico de los gradientes de presión horizontal y, por tanto, de los vientos en áreas de topografía muy inclinada.
La coordenada eta funciona mejor para los flujos alrededor o por encima de las barreras, mientras que la coordenada sigma funciona mejor para flujos que se deslizan por pendientes suaves.
*Ciclogénesis a sotavento con eta y sigma
Eta
Sigma 1
Sigma 2
Verificación
Estas figuras muestran tres pronósticos de 48 horas (generados por un modelo de coordenada eta y dos modelos diferentes de coordenadas sigma) y el análisis de verificación de la presión a nivel del mar para un evento de ciclogénesis a sotavento de una montaña. Examine los pronósticos del centro de baja presión cerca del estado de Kansas generados por los modelos y luego conteste la siguiente pregunta.
Pregunta
¿Qué aspectos de los pronósticos de los modelos de coordenadas eta y sigma exhibe esta guía de modelo operativo para un evento de ciclogénesis a sotavento de una montaña? Escoja todas las opciones pertinentes.
Las respuestas correctas son (a), (d), (e), (h), (i) y (l).
La comparación con el análisis de verificación de la presión a nivel del mar permite ver que uno de los modelos sigma exagera el pronóstico de intensidad de la baja en superficie y ambos modelos sigma colocan la baja muy al norte y al este. Esto es coherente con la tendencia de los modelos sigma de exagerar la intensidad pronosticada de ciclogénesis de sotavento y de iniciarla muy rápidamente (lo cual da al ciclón más tiempo para intensificarse y desplazarse hacia el este). Esto se debe en gran parte a la incapacidad de los modelos de coordenadas sigma de mantener las masas de aire frío a sotavento de las montañas.
La predicción de ciclogénesis obtenida con el modelo eta fue menos intensa y demasiado hacia el sur. Esto es coherente con la incapacidad ocasional de los modelos eta de predecir el flujo de ladera descendente que dispara los eventos de ciclogénesis a sotavento. Es también probable que una representación inadecuada de la topografía y una resolución pobre del aire frío en el modelo hayan contribuido a los errores de pronóstico aquí señalados.
Recuerde que normalmente los modelos de coordenadas eta representan mejor las características del terreno, así como las características y el movimiento de las masas de aire frío en los niveles inferiores. Sin embargo, si el aire frío se retiene durante un período excesivamente prolongado, los pronósticos de los modelos eta pueden exhibir un error de posición, hacia el sur respecto de la realidad, porque desarrollan la depresión en la base de la vaguada de alto nivel y en la extensión sur de la masa de aire frío.
Este ejemplo proviene de modelos antiguos, de resolución más tosca. Conforme aumentan la resolución del modelo y de la topografía empleada en el modelo, estos errores de desplazamiento característicos de los modelos eta y sigma disminuyen y la física del modelo (por ejemplo, cómo el modelo maneja el manto de nieve, las nubes bajas y la mezcla en la capa límite) adquiere relativamente más importancia en términos de la rapidez con que el modelo elimina la masa de aire frío existente en los niveles bajos y descarga vientos descendentes de aire cálido en la ladera a sotavento de las montañas. No obstante, en igualdad de condiciones el modelo que utilice una coordenada vertical que sigue el contorno del terreno creará una baja a sotavento más intensa y más al este en menos tiempo, y cuanto más suave sea la topografía del modelo, tanto más pronunciada será esta tendencia.
*Coordenadas isoentrópicas
*Coordenada isoentrópica
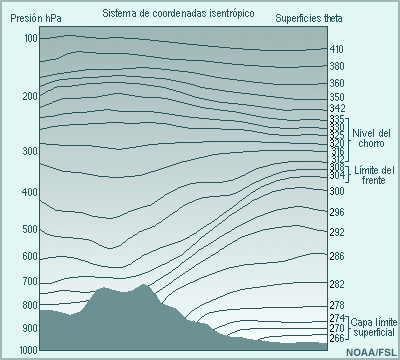
Dado que el flujo en la atmósfera libre es predominantemente isoentrópico, la temperatura potencial (θ) puede ser muy útil como sistema de coordenadas verticales. Sin embargo, los procesos no adiabáticos dominan en la capa límite y las superficies isoentrópicas intersecan la superficie terrestre. Por estas razones, en la actualidad no utilizamos la temperatura potencial sola como coordenada vertical en ningún sistema de modelado numérico operativo. Sin embargo, las coordenadas isoentrópicas son un componente esencial de muchos sistemas de coordenadas verticales híbridos.
*Ventajas de la coordenada isoentrópica
Las coordenadas verticales isoentrópicas brindan muchas ventajas para el diagnóstico de los eventos atmosféricos, muchas de las cuales también se aplican al pronóstico numérico del tiempo.
Ventaja 1: La coordenada theta permite una mayor resolución vertical cerca de las regiones baroclínicas, como los frentes y el límite de la tropopausa.
Theta aumenta más rápidamente con la altura en capas estables. La mayor resolución en estas capas estables e inclinadas (frentes y zonas baroclínicas) permite representar con mayor precisión la cizalladura vertical y horizontal del viento y de las máximas de velocidad de las corrientes en chorro.
Ventaja 2: Cuando el movimiento es adiabático, el aire fluye a lo largo de superficies theta constantes (isoentrópicas) e incluye implícitamente tanto el desplazamiento vertical como el horizontal.
Debido a que en los modelos isoentrópicos la mayor parte del flujo tridimensional en la atmósfera libre se calcula como flujo bidimensional, se necesita menos diferenciación finita en la vertical y se introducen menos errores en los cálculos de advección. Esto permite representar con mucha exactitud la advección de elementos tales como el vapor de agua, porque no se produce la mezcla del aire de las capas de arriba y de abajo.
Ventaja 3: El movimiento vertical a través de las superficies isoentrópicas es causado casi exclusivamente por calentamiento diabático.
El movimiento vertical en los modelos isoentrópicos es el resultado de dos procesos: el movimiento adiabático y el forzamiento diabático. Debido a que las coordenadas isoentrópicas son un sistema «natural» de coordenadas en el cual el flujo adiabático sigue las superficies mismas de las coordenadas, los movimientos adiabáticos verticales se incluyen en la componente «horizontal» de las ecuaciones de pronóstico. La componente vertical de la ecuación de pronóstico isoentrópica está relacionada enteramente con los procesos diabáticos. Al relacionar todo el movimiento vertical exclusivamente con estas componentes adiabáticas y diabáticas se crea una relación de causa y efecto mucho más directa en la interpretación de los campos de pronóstico del modelo.
Ventaja 4: Los modelos de coordenadas isoentrópicas conservan cantidades dinámicas importantes, como la vorticidad potencial.
La capacidad de los modelos isoentrópicos para conservar la vorticidad potencial (VP) es superior a la de cualquier otro sistema de coordenadas porque:
- La vorticidad potencial se conserva muy bien en los flujos adiabáticos de la atmósfera libre.
- Los cambios en la vorticidad potencial están relacionados principalmente con el calentamiento y enfriamiento diabático, que se pueden manejar más directamente con coordenadas isoentrópicas.
La retención de las características dinámicamente importantes asegura un pronóstico cuya dinámica es mucho más coherente que es capaz de capturar procesos de evolución importantes.
*Limitaciones de la coordenada isoentrópica
Las principales limitaciones de las coordenadas isoentrópicas se producen en la capa límite, donde el flujo puede ser fuertemente diabático.
Limitación 1: Las superficies isoentrópicas intersecan el suelo.
Debido a que las superficies isoentrópicas terminan cuando intersecan la superficie terrestre y pueden desplazarse hacia arriba y hacia abajo a través de la superficie terrestre a lo largo del día, no están disponibles para los cálculos en todo momento y en todo lugar, y además su comportamiento no se puede modelar fácilmente. Las coordenadas theta suelen utilizarse en combinación con las coordenadas sigma cerca del suelo, para que por lo menos la primera capa del modelo siga la superficie del terreno.
Limitación 2: Es posible que las coordenadas isoentrópicas no exhiban un comportamiento monotónico con la altura, especialmente en la capa límite.
Las capas superadiabáticas se pueden desarrollar en cualquier parte de la atmósfera, pero se producen predominantemente en la capa límite, debido al calentamiento diurno. Cuando se desarrollan, las superficies isoentrópicas aparecen más de una vez en el perfil vertical sobre un punto, algo que no se puede permitir en el sistema de coordenadas verticales de un modelo. Aunque se pueden efectuar ajustes numéricos para limitar la ocurrencia de capas inestables, esto puede limitar seriamente la capacidad del modelo de pronosticar muchas situaciones atmosféricas.
Limitación 3: La resolución vertical en capas casi adiabáticas es gruesa.
La misma característica que lleva a una mejor resolución en las zonas baroclínicas también provoca la disminución de la resolución vertical en regiones adiabáticas grandes (las cuales a menudo se observan como sondeos con gradientes de temperatura casi iguales al gradiente adiabático seco y son importantes en los procesos de mezcla vertical) cuando se utiliza theta como coordenada vertical. Esto puede causar problemas relacionados con la resolución adecuada de la mezcla vertical que se produce en estas regiones.
Las superficies isoentrópicas tienen pendientes empinadas cerca de las regiones de fuerte baroclinicidad, como los frentes. Sin embargo, las fuertes pendientes en las coordenadas isoentrópicas no producen las mismas inexactitudes en el cálculo del gradiente de presión horizontal genera la coordenada sigma, y es producto de aprovechar las fuertes limitaciones dinámicas asociadas con el uso de coordenadas naturales, es decir, coordenadas relacionadas dinámicamente con el flujo. Por tanto, incluso en las zonas frontales donde las isoentropas pueden presentar una pendiente considerable, el pronóstico del viento geostrófico y, por tanto, del viento ageostrófico, no sufre mucho.
*Pregunta sobre la coordenada isoentrópica
Pregunta
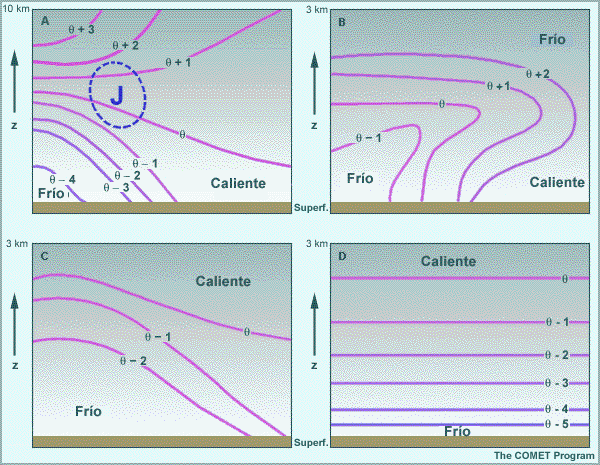
¿Cuáles de estos paneles muestran patrones de tiempo problemáticos para los modelos de coordenadas verticales isoentrópicas? Escoja todas las opciones pertinentes.
Las respuestas correctas son A, B y C. La capa límite inestable arriba de la intrusión superficial caliente en el lado izquierdo de la figura B crea superficies theta que no varían monotónicamente con la altura. La situación en las parcelas A y C muestra superficies theta que penetran el suelo en los bordes de la bolsa de aire frío, también una característica indeseable.
En la descripción de la masa de aire frío en los niveles inferiores, el panel D revela una de las ventajas de las coordenadas verticales isoentrópicas: las superficies theta pueden describir la extensión del aire frío cerca de la superficie con mayor resolución gracias al mayor gradiente vertical theta en el aire frío de bajo nivel. La parte superior del panel A también muestra la ventaja de las coordenadas isoentrópicas de aumentar la densidad de las superficies de coordenadas cerca de los frentes de alto nivel y los máximos de velocidad de la corriente en chorro.
Coordenadas híbridas
Coordenadas híbridas
Para mejorar los esfuerzos de modelado, se ha experimentado con el uso de distintas combinaciones de parámetros como sistemas de coordenadas verticales. En 1979, Uccellini et al. presentaron avances importantes que aumentaron la posibilidad de utilizar un sistema híbrido de coordenadas verticales isoentrópicas-sigma. Este sistema, que fue perfeccionado por Bleck y Boudra en 1981 y Bleck y Benjamin en 1993, se ha utilizado en el modelo operativo RUC de NCEP, aunque no formará parte de su sucesor, el modelo Rapid Refresh. Los modelos GFS y NAM utilizan sistemas híbridos de coordenadas σ-p en los cuales las superficies sigma empleadas cerca del suelo se transforman en superficies de presión en la parte superior de la atmósfera.
Híbrido sigma-presión
En los modelos híbridos de coordenadas sigma-presión se utilizan superficies sigma en la parte inferior del modelo que se transforman en superficies isobáricas en altura. Este esquema aprovecha la capacidad de la coordenada sigma de ajustarse al suelo en la capa límite al tiempo que hace uso de coordenadas más planas con mejores propiedades numéricas en altura, lo cual aumenta la eficiencia y exactitud de los cálculos de transferencia radiativa empleados para asimilar las observaciones de radiancia satelital. La troposfera y la estratosfera son esenciales en la asimilación de las observaciones de radiancia de los satélites, que por su enorme abundancia desempeñan un papel dominante en la asimilación de datos.
Ciertos modelos, como el NAM en 2009 (que en determinado momento puede cambiar) tienen un dominio sigma puro debajo de una presión de transición fija, arriba de la cual todas las capas son exactamente isobáricas. Sin embargo, otros modelos, como se ilustra a continuación para GFS, utilizan una fusión gradual, de modo que la coordenada realiza una transición gradual de la coordenada sigma en los niveles inferiores a coordenadas isobáricas en los niveles más altos. El método de fusión gradual elimina los artefactos numéricos que se observan en el nivel de transición de los pronósticos de algunos modelos que pasan repentinamente de sigma a presión.
Haga clic en las imágenes para ver versiones más grandes:
La coordenada sigma se muestra en colores naranja junto a la coordenada híbrida gris. Observe la diferencia sobre topografía compleja (empinada) a cualquier altura, incluso las montañas bajas en 80° W: el sistema híbrido es mucho más plano en la troposfera superior. Sobre topografía relativamente plana, las dos coordenadas casi coinciden.
Ventajas de sigma-presión
El sistema híbrido de coordenadas verticales sigma-presión ofrece muchas ventajas.
Ventaja 1: En la troposfera superior, donde a menudo se encuentran los gradientes de presión más fuertes, este sistema evita las dificultades de cálculo numérico que presentan las coordinadas sigma sobre terreno empinado.
Ventaja 2: Este sistema permite hacer un mejor uso de las observaciones de radiancia de los satélites que una coordenada sigma.
Ventaja 3: Representa bien el calentamiento superficial y la mezcla dinámica en la capa límite.
Ventaja 4: Permite modelar bien las interacciones físicas en la superficie, incluyendo la evaporación superficial y el tratamiento del manto de nieve.
Limitaciones de sigma-presión
Limitación 1: Los errores de cálculo de la fuerza del gradiente de presión ocasionadas por la coordenada sigma también existen en este sistema híbrido, en la troposfera inferior, y a veces hasta en la troposfera media.
Limitación 2: Aunque sigue siendo necesario suavizar el terreno como para las coordenadas sigma, quizás no se necesite en el mismo grado.
Limitación 3: Los vientos catabáticos excesivos y el desarrollo demasiado rápido de la ciclogénesis a sotavento característicos de la coordenada sigma existen en este sistema híbrido.
Limitación 4: Puede ser difícil fusionar los tipos de coordenadas en sus interfases.
Es esencial que haya una interacción plena a lo largo de la interfase de los dos dominios de coordenadas verticales que muestre los procesos atmosféricos de forma realista, sin introducir valores espurios de masa, momento o fuentes de energía. Esto puede ser difícil de lograr numéricamente. En este respecto, el sistema de fusión gradual produce los mejores resultados, aunque no permite usar niveles puramente isobáricos en la troposfera media y alta.
*Híbrido isoentrópico-sigma
En los modelos híbridos de coordenadas isoentrópicas-sigma, se utilizan superficies sigma en la parte inferior del modelo que se transforman en superficies isoentrópicas con la altura. La unión de las coordenadas theta y sigma en un sistema de coordenadas verticales combina la ventaja de adaptación al terreno de la coordenada sigma con la mejor resolución vertical de las superficies isoentrópicas en áreas baroclínicas clave, que es una característica de las coordenadas isoentrópicas, o theta. Esta solución eficaz permite contrarrestar algunas de las limitaciones de cada sistema individual.
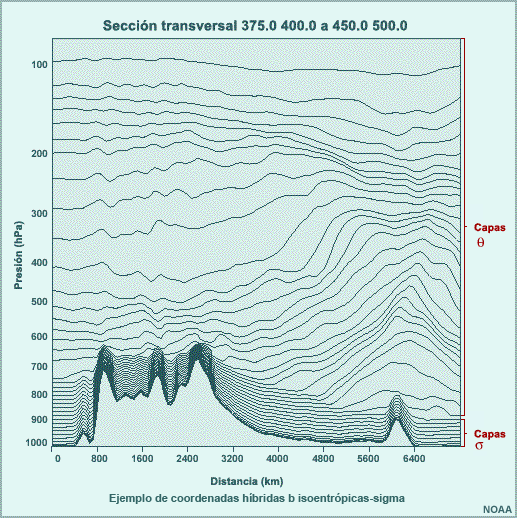
La capa límite sigma debe ser lo suficientemente profunda como para poder modelar los procesos de capa límite diurnos, incluyendo la fricción y el calentamiento. En términos generales esto implica una capa límite sigma de una profundidad aproximada de 200 hPa. Si la capa sigma es demasiado poco profunda, pueden aún formarse capas superadiabáticas, o el modelo no las manejará apropiadamente más allá del límite del dominio sigma.
*Ventajas del modelo híbrido isoentrópico-sigma
El sistema híbrido de coordenadas verticales isoentrópicas-sigma ofrece muchas ventajas.
Ventaja 1: Mantiene las ventajas de los modelos isoentrópicos en la atmósfera libre, incluyendo mejores momentos de inicio de la precipitación para ascenso isoentrópico (advección cálida) que los modelos de coordenadas sigma.
Ventaja 2: Elimina el problema de la intersección de las superficies isoentrópicas con el suelo.
Ventaja 3: Representa bien el calentamiento superficial y la mezcla dinámica en la capa límite.
Ventaja 4: Permite modelar bien las interacciones físicas en la superficie, incluyendo la evaporación superficial y el tratamiento del manto de nieve.
El sistema híbrido de coordenadas verticales isoentrópicas-sigma permite modelar adecuadamente los procesos de una capa límite convectivamente inestable mediante la coordenada sigma y, a la vez, aprovechar las ventajas de la naturaleza adaptativa de theta cerca de las regiones baroclínicas, como los frentes y la tropopausa.
Arriba de la capa límite, donde el flujo es primordialmente adiabático, se ha demostrado que la advección vertical (que suele sufrir más de los errores de truncamiento que la advección horizontal) «trabaja» mucho menos en estos modelos híbridos que en los modelos sigma o eta. Esto se debe a que la componente adiabática del movimiento vertical en las superficies theta se captura en el flujo a lo largo de las superficies bidimensionales. El resultado es un mejoramiento del transporte de humedad y pocos problemas de inicialización de la precipitación en las primeras horas del pronóstico cuando los procesos dinámicos que fuerzan los eventos meteorológicos se hallan principalmente arriba de la capa límite. La precipitación de frente caliente a escala de malla comienza a tiempo, incluso cuando ocurre tarde en el período de predicción, sin el atraso que producen los modelos de coordenadas sigma (Johnson et al. 1993).
*Limitaciones del modelo híbrido isoentrópico-sigma
Limitación 1: Los modelos híbridos isoentrópico-sigma no conservan el flujo adiabático en la capa límite tan fácilmente como los modelos isoentrópicos puros.
El flujo adiabático no se puede conservar en los niveles inferiores (donde se utiliza la coordenada sigma), aun cuando eso pueda resultar ventajoso. Un ejemplo es el flujo sobre frentes poco profundos. Para simular el flujo sobre el frente, la coordenada sigma debe utilizar diferencias verticales finitas en los términos de advección vertical y termina mezclando numéricamente parte del gradiente frontal. Este problema también es pertinente para el deslizamiento de la humedad sobre el frente en una capa de naturaleza isoentrópica ubicada en la porción de coordenadas sigma del modelo.
Limitación 2: La profundidad de las capas sigma no coincide con la verdadera profundidad de la capa límite planetaria, de modo que este sistema de coordenadas no es el más apropiado para describir los procesos que se producen cerca de la interfase entre la capa límite y la atmósfera libre.
El flujo adiabático inmediatamente arriba de la capa límite planetaria no se puede describir mediante coordenadas isoentrópicas porque se produce dentro del dominio de las coordenadas verticales sigma. Un ejemplo es el desarrollo del chorro nocturno de bajo nivel que se forma en las Grandes Llanuras de Estados Unidos. Si la capa sigma es más profunda que la delgada capa límite nocturna, la mayor mezcla que se produce en la capa de coordenadas sigma puede reducir la intensidad del chorro de bajo nivel pronosticado y producir errores en su posición vertical. El desarrollo subsiguiente de convección nocturna, que depende de la advección y de la convergencia de humedad que resulta del chorro, puede ser subpronosticado.
Alternativamente, la capa límite planetaria puede ser tan profunda que la capa superficial mezclada se extiende por encima de la región sigma del modelo. En consecuencia, las coordenadas isoentrópicas se terminan utilizando en la parte superior de una capa límite bien mezclada. Ya se ha mencionado la debilidad de las coordenadas isoentrópicas en las regiones adiabáticas.
Debido a que a veces la profundidad de la capa sigma no puede coincidir con la profundidad de la capa límite planetaria, puede suceder que los eventos de flujo adiabático por encima de la capa límite planetaria real pero por debajo de la capa sigma superior queden distribuidos a través de varias capas isoentrópicas.
Limitación 3: Puede ser difícil fusionar los tipos de coordenadas en sus interfases.
Es esencial que haya una interacción plena a lo largo de la interfase de los dos dominios de coordenadas verticales que muestre los procesos atmosféricos de forma realista, sin introducir valores espurios de masa, momento o fuentes de energía. Esto puede ser difícil de lograr numéricamente.
Modelos no hidrostáticos de alta resolución
El requisito de que los modelos no hidrostáticos resuelvan una ecuación de pronóstico del movimiento vertical limita la elección de la coordenada vertical y aumenta el tiempo de cómputo, y esto compite con la resolución horizontal y vertical para el uso de los recursos computacionales. El resultado es que:
- La mayoría de los modelos no hidrostáticos utilizan una coordenada vertical basada en la altura (unos pocos se basan en la presión y ninguno utiliza coordenadas isoentrópicas). Las formulaciones eta y sigma se pueden utilizar, teniendo en cuenta sus limitaciones normales.
- Algunos modelos de pronóstico y de uso local no hidrostáticos sacrifican la resolución vertical para que el modelo se pueda ejecutar en tiempo real con una resolución horizontal fina. Esto no representa un problema grave para los estudios de investigación de convección profunda, pero limita su utilidad para el pronóstico detallado de estructuras en la capa límite, capas delgadas de humedad introducidas en zonas baroclínicas inclinadas y la estructura detallada en y por encima de la región de la tropopausa. Conviene fijarse en la cantidad y distribución de las capas empleadas en los modelos utilizados para el pronóstico.
- Típicamente, la razón de resolución vertical a resolución horizontal es pobre. Por lo tanto, la inclinación de algunas estructuras, como las zonas baroclínicas, no se puede representar bien porque la resolución horizontal fina fija la ubicación horizontal, mientras que la ubicación vertical queda sujeta a grandes errores de diferencias finitas. Esta incoherencia puede introducir ruido numérico en el pronóstico y reduce las ventajas de los modelos no hidrostáticos en el pronóstico de sistemas baroclínicos.
Preguntas
Pregunta 1
Pregunta
Asocie cada sistema de coordenadas verticales con su principal ventaja en términos de la representación del tiempo en los modelos de predicción numérica. Use el cuadro de selección para elegir la mejor respuesta para el enunciado.
Tanto la coordenada sigma como la coordenada híbrida sigma-presión sigue el contorno del terreno, lo cual permite a ambas resolver bien la capa límite en todas las condiciones meteorológicas. Sin embargo, las coordenadas híbridas sigma-presión son más planas en la troposfera media a alta y en la estratosfera arriba de terreno complejo, lo cual facilita la asimilación de las observaciones de radiancia de los satélites. Al igual que el análisis de los datos en coordenadas isoentrópicas nos ayuda a diagnosticar corrientes de aire, humedad, movimientos verticales y estructuras en chorro en entornos baroclínicos, con las coordenadas isoentrópicas el modelo puede mejorar la resolución vertical cerca de frentes y corrientes en chorro, donde las superficies de las coordenadas quedan apretadas.
Pregunta 2
Pregunta
Asocie cada sistema de coordenadas verticales con su desventaja principal para la representación del tiempo en los modelos de predicción numérica. Use el cuadro de selección para elegir la mejor respuesta para el enunciado.
Tanto la coordenada sigma como la coordenada híbrida sigma-presión sigue el contorno del terreno (normalmente terreno suavizado), debido a lo cual resulta difícil mantener el estancamiento o embolsamiento de aire frío a la vez que evoluciona una baja a sotavento. En realidad, ambos sistemas tienen una resolución vertical más fina sobre terreno en altura, ya que el mismo número de niveles del modelo quedan apretados en una columna menos profunda. Las coordenadas isoentrópicas no pueden manejar las condiciones superadiabáticas, porque la misma temperatura potencial aparecería en dos niveles distintos, por encima y por debajo de la capa superadiabática. Las capas límite superadiabáticas son comunes por la tarde, motivo por el cual la mayoría de los modelos que utilizan coordenadas isoentrópicas emplean un sistema híbrido con coordenadas sigma en la capa límite.
Resumen
Todos los sistemas de coordenadas verticales utilizados en los modelos de pronóstico numérico del tiempo tienen ventajas y desventajas, tanto de naturaleza computacional como meteorológica. Para interpretar mejor la salida del modelo, es útil saber qué sistema utilizan los distintos modelos y entender los puntos fuertes y las limitaciones de cada sistema en la aplicación a diferentes fenómenos del tiempo y circunstancias meteorológicas.
| Coordenada vertical | Modelos | Ventaja principal | Limitación principal |
|---|---|---|---|
| Híbrida genérica | ECMWF, GFS, NAM, WRF-NMM | Combina los puntos fuertes de varios sistemas de coordenadas. | Es difícil manejar la interfase entre los dominios de las coordenadas. |
| Híbrida isoentrópica-sigma (θ-σ) | RUC, hasta que se reemplace con Rapid Refresh (anticipado para 2010) | Aumenta en forma natural la resolución en zonas baroclínicas, como en frentes y la tropopausa. | Describe de forma incompleta los flujos adiabáticos importantes de bajo nivel. |
| Sigma (σ) | WRF-ARW, muchos modelos de investigación | Las superficies siguen el contorno del terreno y, por lo tanto, describen bien la capa límite. | Es posible que no represente correctamente las condiciones atmosféricas a sotavento de las montañas. |
Resolución horizontal
Introducción
La resolución horizontal de un modelo numérico de predicción del tiempo está relacionada con la distancia entre los puntos de malla, en el caso de un modelo de malla, o con el número de ondas que se pueden resolver, en el caso de un modelo espectral. Para nuestros propósitos, «resolución» se define en términos de la distancia entre puntos de malla o del número de ondas, y representa el área promedio que describe cada punto de malla o el número de ondas utilizadas, según el tipo de modelo de que se trate. Observe que las estructuras más pequeñas que un modelo puede representar con exactitud son varias veces más grandes que la «resolución» de la malla. De hecho, no es posible representar o pronosticar fenómenos de dimensiones de la misma escala que el espaciado de la malla.
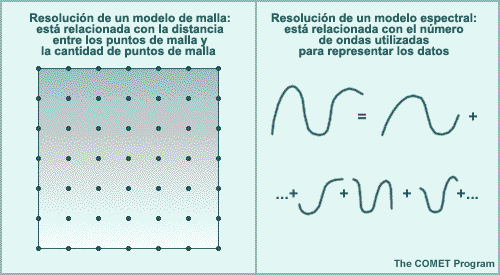
Si bien la resolución horizontal juega un papel clave en la habilidad del modelo para resolver características, otros factores, como la resolución vertical, las coordenadas verticales y el paquete de física, también tienen un impacto significativo.
Espaciado de malla y resolución
La resolución horizontal de un modelo de malla se define como la distancia media entre puntos de malla adyacentes que utilizan las mismas variables. Por ejemplo, si todas las variables de pronóstico de un modelo (componente u del viento, componente v del viento, temperatura y humedad, etc.) se pronostican en cada uno de los puntos de la malla (como en la figura), se considera que el modelo tiene una resolución igual a la distancia mínima entre los puntos de malla adyacentes en una latitud y longitud específica. En el ejemplo, todas las variables se calculan en cada punto de la malla, de modo que la resolución es 50 km. Un modelo similar con una distancia de 10 km entre puntos de malla adyacentes tendría una resolución horizontal de 10 km. ¡Pero eso no significa que es capaz de resolver estructuras de 10 km de ancho! Como veremos más adelante, un modelo con una «resolución horizontal de 10 km» apenas logra detectar estructuras de 20 km de ancho y puede hacer predicciones razonables para fenómenos de 50 a 70 km, mejor aún si abarcan 100 km.
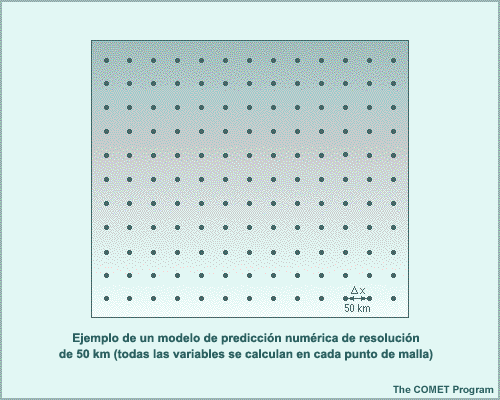
Que un modelo se considere de alta o baja resolución depende del tamaño del dominio y de la escala de los fenómenos atmosféricos que el modelo pretende pronosticar. Una resolución del orden de 20 a 50 km se considera alta para un modelo global, mientras que para un modelo de la escala de una tormenta una resolución de 100 a 500 m se considera alta y necesaria para resolver los procesos de convección internos.
Categorizar los modelos por su resolución (alta o baja) realmente no es útil, porque se trata de un término relativo que cambia siempre que aparecen nuevos modelos. Independientemente de su dominio, un modelo que hoy se considera de alta resolución puede pasar a ser un modelo de baja resolución mañana.
Resolución espectral
En los modelos espectrales, la resolución horizontal se designa anteponiendo la letra «T» a un número (por ejemplo, T80) que indica la cantidad de ondas utilizadas para representar los datos. La «T» es una referencia a truncamiento triangular, que indica el conjunto particular de ondas empleadas por el modelo espectral.
Los modelos espectrales representan los datos de forma precisa hasta un número máximo de ondas, pero omiten toda la información más detallada contenida en las ondas más pequeñas. Esta representación exacta hasta cierto punto después del cual se produce la omisión completa contrasta con el funcionamiento de los modelos de malla, los cuales tratan de representar todas las escalas, pero no manejan bien las ondas que solo abarcan unos cuantos puntos de malla.

La longitud de onda de la onda más pequeña en un modelo espectral es representada por
Longitud de onda mínima = 360 grados/N
donde N es el número total de ondas (el número «T»).
Surgen complicaciones cuando se hacen cálculos dinámicos y físicos no lineales en una malla que luego se convierten al formato espectral para incorporar sus efectos en un modelo espectral. Debido a los errores que se introducen, el resultado final es menos exacto de lo que sería de esperar si los cálculos se hubieran realizado estrictamente en el espacio espectral.
Equivalencia de resol. espectral y de malla
Aunque los modelos de malla pueden incorporar datos de cualquier resolución, a veces pueden introducir errores al hacerlo. Se necesitan entre cinco y siete puntos de malla para obtener aproximaciones razonables de la mayoría de las estructuras atmosféricas. Es común que se necesiten incluso más puntos por estructura de onda para obtener un buen pronóstico. Debido a que los modelos espectrales y de malla conservan la información de forma diferente, no es posible especificar una distancia entre puntos de malla equivalente a una determinada resolución espectral. Sin embargo, existe un método muy sencillo para llegar a una aproximación de la densidad de malla necesaria para obtener un nivel de exactitud equivalente al de un modelo espectral con un determinado número de ondas. En primer lugar, supongamos que tres puntos de malla son suficientes para capturar la información contenida en una serie de ondas continuas. El espaciado de malla aproximado que permite lograr la misma exactitud que un modelo espectral se puede estimar con la siguiente ecuación:
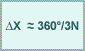
Para un modelo T80, esto produce una distancia máxima entre puntos de malla para una exactitud equivalente de:
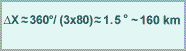
De hecho, la dinámica de los modelos espectrales logra una representación de las ondas mucho mejor que los modelos de malla con este espaciado de malla. Sin embargo, la física de los modelos espectrales se calcula sobre una malla que utiliza aproximadamente tres puntos de malla por cada onda utilizada para representar los datos. Dado que se necesitan entre cinco y siete puntos de malla para representar bien los datos «ondulados» y todavía más para las estructuras que incluyen discontinuidades, la resolución de la física es más pobre de lo que indica la formulación anterior y, por lo tanto, la calidad del pronóstico del modelo espectral se degrada.
En resumen, los modelos espectrales funcionan bien con ondas «secas» en la atmósfera libre, pero su representación de la física, incluyendo propiedades de superficie, es más gruesa. La calidad general del pronóstico final está entre estos dos extremos y varía de un caso a otro. Mientras más física esté involucrada en la evolución del pronóstico, menor será la ventaja de los pronósticos generados por un modelo espectral respecto a los pronósticos de un modelo de malla de resolución comparable.
Topografía y litorales
Orografía en el modelo
Dos factores limitan la representación de la orografía en el modelo:
- la resolución horizontal del modelo;
- la resolución horizontal del conjunto de datos del terreno.
Si el conjunto de datos del terreno es grueso o aproximado, no podrá proporcionar a un modelo de alta resolución los detalles topográficos que necesita. Si el modelo no puede resolver las características topográficas, los detalles provistos por el conjunto de datos del terreno se promedian. En la mayoría de los casos, cierto grado de suavizado del terreno es deseable, en parte porque el flujo de aire sobre terreno complejo genera ruido de pequeña escala que puede encubrir la señal de gran escala.
Topografía en el modelo y en la realidad
Como ya vimos, tanto la resolución del modelo como el suavizado de la topografía influyen en la representación de la superficie por el modelo. Los siguientes mapas ilustran los efectos de la resolución y el suavizado de la topografía en el modelo en comparación con el terreno real.
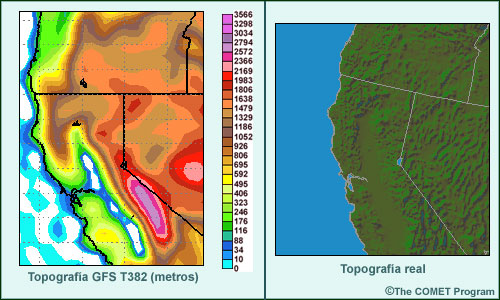
Entre las imperfecciones más comunes en la representación de la topografía en el modelo cabe mencionar:
- La elevación de las cumbres de las montañas más altas suele ser menor que en la realidad.
- A menudo, los valles no se representan o se representan con menos diferencia de elevación entre los picos y el fondo de los valles que en la realidad (es decir, los valles «se llenan»).
- La elevación de los sistemas montañosos se distribuye sobre un área horizontal excesivamente amplia, lo cual se debe a promediar el terreno en cada celda de la malla.
- Los gradientes de elevación se subestiman, especialmente en regiones de terreno muy inclinado y complejo.
Topografía: consideraciones para el pronóstico
La representación de la topografía de la superficie por el modelo determina su capacidad de pronosticar las estructuras meteorológicas inducidas por el terreno. Como se ilustra a continuación, si un modelo no representa un accidente topográfico, no puede resolver o pronosticar un fenómeno meteorológico inducido o influenciado por esa estructura topográfica. Los modelos tienen problemas de resolución, especialmente en regiones de terreno complejo, como el oeste de los Estados Unidos, Alaska, Hawái e incluso los Apalaches.
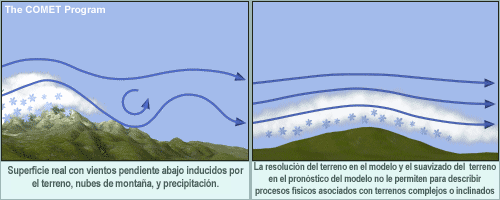
En el ejemplo, se está produciendo un evento de viento de ladera descendente y nieve a barlovento de la montaña sobre una región de topografía inclinada y compleja. La topografía se ha suavizado para dar al modelo de malla hipotético cierta estabilidad computacional, pero eso significa que el modelo no puede describir con exactitud los procesos físicos que están ocurriendo en la realidad. Lo más probable es que el modelo no pueda pronosticar el evento catabático, ni el rotor del viento, ni la sombra de lluvia. Como resultado, las nubes a barlovento y la precipitación se esparcirán sobre un área más grande y serán de menor intensidad que en la realidad. El resultado sería el mismo si un modelo de resolución gruesa utilizara un conjunto de datos topográficos detallados o si un modelo de resolución fina utilizase un conjunto de datos topográficos poco detallados.
¿Por qué no se ejecutan modelos de malla de alta resolución con características detalladas del terreno a la misma escala que la distancia entre puntos de malla? La respuesta es que las ondas a una escala de unos cuantos puntos de malla se representan mal y se pronostican aún peor. Además, a medida que la energía se acumula en los modelos a escalas de tres puntos de malla o menos, los métodos computacionales pueden «estallar» y detener la ejecución del modelo antes de que termine de generar un pronóstico. Por lo tanto, es preciso suavizar la topografía para impedir que se produzcan estas ondas de pequeña escala.
Impactos de la representación del terreno en el modelo
Pregunta
¿Cuáles son algunos de los posibles efectos de una representación topográfica inadecuada en el modelo para los elementos meteorológicos? Escoja todas las opciones pertinentes.
Las respuestas correctas son (a), (c), (d), (f), (g) y (h). En términos generales, una representación inadecuada de la superficie por el modelo influye adversamente en su capacidad de pronosticar características y procesos inducidos o modificados por el terreno.
El gráfico que sigue muestra el pronóstico de 12 a 36 horas del modelo GFS de las 00 UTC del 3 de marzo de 2009 y el análisis de verificación del Centro de Predicción Hidrológica (Hydrologic Prediction Center, HPC) de EE.UU. Para que la comparación fuera justa, proyectamos el cálculo estimado de la precipitación observada y el pronóstico del modelo sobre la misma malla de 32 km, como suele hacerse al calcular las estadísticas de verificación de la precipitación. De no proceder de esta forma, el cálculo estimado de la precipitación observada exhibiría mucha más definición y máximos mucho más altos. En la segunda figura, la topografía del modelo GFS para esta región se yuxtapone a un mapa topográfico detallado.
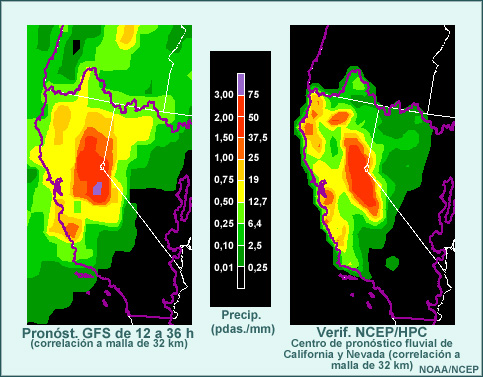

Note estas características importantes:
- La precipitación observada cayó principalmente sobre los dos sistemas montañosos.
- Los máximos de precipitación pronosticados por el modelo se extendieron a los valles, donde en realidad cayó poca lluvia.
- El modelo pronosticó máximos de precipitación demasiado bajos junto a las montañas de la costa del norte de California, pero cantidades similares a los máximos observados en la Sierra Nevada. Los estimados de la precipitación observada elaborados por el Centro de Pronósticos Fluviales (River Forecast Center, RFC) sobre una malla mucho más fina (que no se incluye aquí) mostraron zonas delgadas y elongadas de 75 a 100 mm.
- La ubicación de los máximos de precipitación pronosticados no coincide exactamente con el terreno más elevado ni los gradientes más empinados del modelo.
A menudo, la lluvia registrada en pluviómetros y los análisis de escala fina basados en informes de pluviómetros muestran cantidades máximas mayores de las del pronóstico del modelo, que representa un promedio sobre una celda de malla (recuerde que incluso los modelos espectrales calculan la precipitación sobre una malla de transformación). El análisis de las observaciones puede incluso estar sesgado hacia valores más altos, si los pluviómetros se ubican intencionalmente en lugares de altura en los que se sabe que la precipitación es alta, por ejemplo para fines de monitoreo hidrológico.
Precipitación y orografía en el modelo
Este caso, un evento de fuerte precipitación en la cuenca de Los Ángeles, ilustra el efecto de aumentar la resolución y representar la topografía con mayor detalle. Para obtener pronósticos exactos de la ubicación y cantidad de precipitación, tanto el modelo como los conjuntos de datos topográficos empleados por el modelo deben ser de alta resolución.
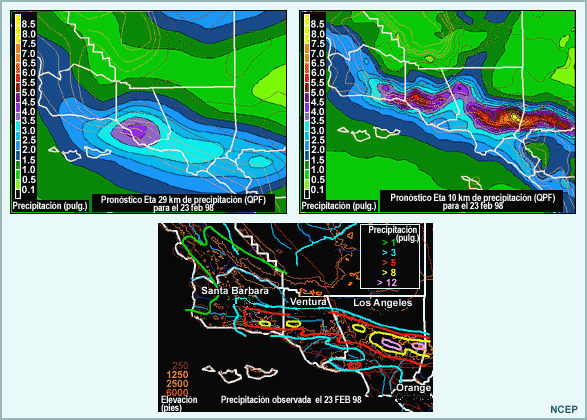
Los paneles superiores muestran los pronósticos de precipitación de los modelos Eta de 29 km y 10 km, mientras el panel inferior muestra la precipitación observada, para un caso de flujo hacia tierra que causó un intenso levantamiento orográfico de una masa de aire húmedo. Sin contar la resolución, los modelos son idénticos y los pronósticos se iniciaron con las mismas condiciones de base. La resolución topográfica es mejor en el modelo de 10 km que en el de 29 km, lo cual se refleja en una mejor ubicación de la precipitación, especialmente para las cantidades mayores. Además, las cantidades de precipitación pronosticadas por el modelo de 10 km se parecen más a los valores observados.
Un elemento clave del éxito del pronóstico del modelo de resolución más alta es que el forzamiento fue intenso y se produjo con un patrón espacial fijo y conocido, es decir, determinado por la topografía. Cuando la precipitación no queda anclada al terreno o a los litorales (es decir, inducida por brisas marinas), los modelos de alta resolución pueden producir estructuras de precipitación intensa realistas en el lugar incorrecto, e incluso estructuras que no se verifican en absoluto.
Interfase tierra/agua
Los modelos también tienen dificultad para resolver estructuras influenciadas o causadas por las zonas de contacto entre las masas de tierra y los cuerpos de agua grandes. Esto incluye las regiones costeras oceánicas y aquellas cercanas a los lagos grandes. Dada la gran diferencia en las propiedades de la tierra y del agua, un modelo cuya resolución no es suficiente para determinar su ubicación representará mal los procesos en los que influyen o que ocurren en las zonas de contacto entre tierra y agua. Por ejemplo, los Grandes Lagos de América del Norte no están bien definidos en algunos modelos globales y regionales debido a una resolución horizontal insuficiente. En otros casos, el posible que el modelo coloque la zona de contacto entre tierra forme y mar en el lugar incorrecto, o que defina inadecuadamente sus límites. Los lagos menores se reconocen solo en los modelos de mesoescala y de escala local de resolución muy fina y no se representan en la mayoría de los modelos operativos.
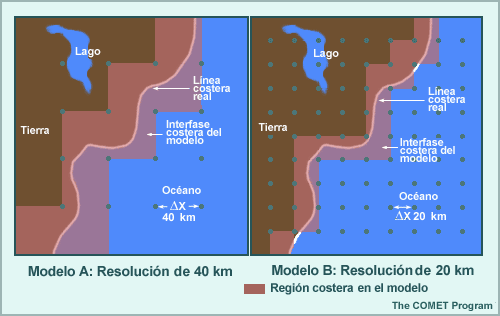
En el ejemplo, la línea costera en los modelos A y B se encuentra dentro de las regiones sombreadas en morado. En el modelo A, la mayor parte de las áreas de contacto entre agua y tierra queda dentro de una banda de 40 km, las irregularidades de la línea costera real no quedan bien representadas y el lago no se reconoce en absoluto. En el modelo B, en la mayoría de los lugares el área de contacto entre agua y tierra se encuentra dentro de una banda de 20 km, las irregularidades de la línea costera real están mejor representadas y hay tres puntos de malla que identifican el lago.
El ejemplo muestra por qué los modelos con una resolución insuficiente no se desempeñan a la hora de definir estructuras y procesos tales como las brisas y los frentes de mar y de lagos, las bandas de nieve por efecto lago y los frentes costeros.
Al incrementar la resolución horizontal, es posible definir mejor la zona de contacto costera y las diferencias entre las propiedades superficiales de tierra firme y las masas de agua. A su vez, esto contribuye a que el modelo resuelva mejor las características y los procesos meteorológicos asociados con estas zonas de contacto.
Ej. de brisa lacustre
Muchos fenómenos de pequeña escala importantes para el pronóstico local no se pueden resolver en la malla del modelo. Este ejemplo ilustra una circulación de brisa lacustre. El panel de la izquierda muestra los ecos en aire claro de un radar Doppler del Servicio Nacional de Meteorología (National Weather Service, NWS) de EE.UU., que indican la presencia de un frente de brisa lacustre sobre el sureste del estado de Wisconsin. El panel de la derecha muestra la ubicación del frente de brisa lacustre superpuesto a la malla de 12 km utilizada en el modelo NAM de NCEP en 2009. Observe que la estructura de convergencia y movimiento vertical del frente de brisa lacustre que revela el radar es mucho más pequeña que una celda de la malla. Claramente, la resolución del modelo no permite predecir con exactitud la estructura e intensidad del movimiento vertical asociado a fenómenos de una escala tan pequeña. La resolución mucho más gruesa de un miembro del conjunto de un modelo global ni siquiera lograría generar la brisa lacustre en la región correcta, aunque trataría de producir un poco de circulación dado un lago Michigan frío y una masa continental cálida al oeste.
Fíjese además en la forma de la costa en el modelo. Hay lugares sobre tierra firme donde el modelo muestra agua y lugares sobre el agua donde el modelo ha creado un promontorio de hasta 12 km de ancho. Esto afectará en gran medida los pronósticos locales de temperatura de superficie, así como la posición y la forma de la brisa lacustre en el pronóstico del modelo. Si bien un modelo de resolución fina no presentará el litoral a la perfección, un modelo de resolución gruesa puede representarla con errores muy grandes, incluso peor que en el ejemplo de resolución de 12 km que acabamos de ver.
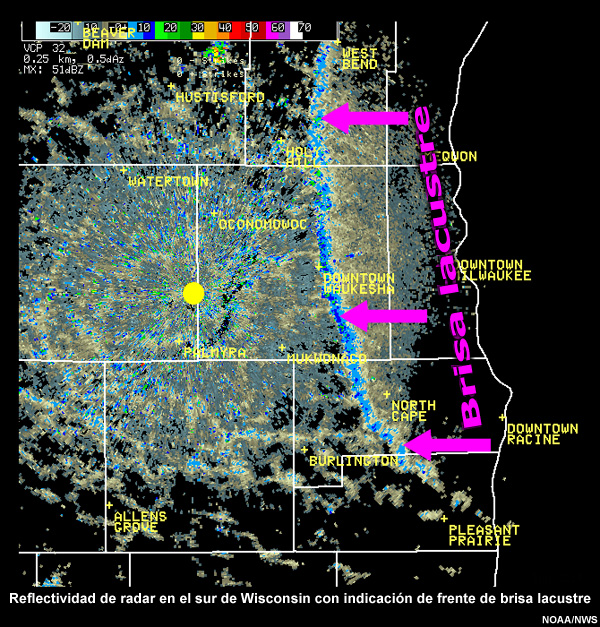
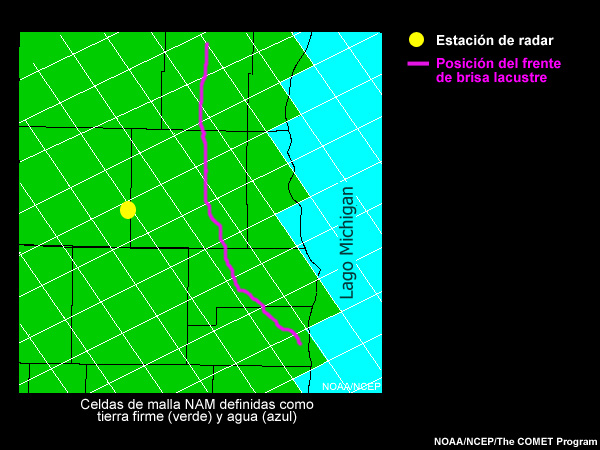
*Recursos de cómputo
*Introducción
Desde los albores de la predicción numérica del tiempo, las necesidades de cálculo han forzado los límites de la capacidad de cómputo disponible. Para completar un pronóstico, las ecuaciones de muchas variables y millones de puntos de malla se deben resolver hasta miles de veces, para un total acumulado de casi un billón (1012) de actualizaciones para cada variable de pronóstico. La cantidad total de cálculos es mucho mayor, porque algunos cálculos físicos son muy complejos y los cálculos de dinámica también implican una serie de pasos.
En última instancia, los recursos de cómputo limitan la resolución de los modelos de PNT. Los recursos de cómputo adicionales que se requieren para ejecutar un modelo mejorando su resolución horizontal al doble sin cambiar la resolución vertical o el tamaño del dominio, incrementan en un factor de ocho.
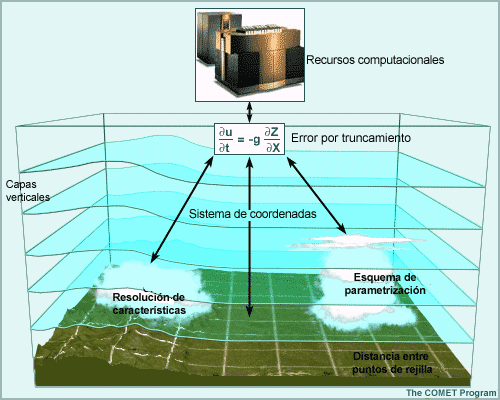
*Aumento de resolución
Cuando se aumenta la resolución de un modelo, se incrementa la demanda en los recursos computacionales, porque el modelo debe determinar los valores para una mayor cantidad de puntos de malla. Como se ilustra a continuación, si reducimos la distancia entre los puntos de malla del modelo se reduce a la mitad (mayor resolución), el número de puntos de malla sobre la misma área se cuadruplica. Sin embargo, las consecuencias son aún mayores. El paso de tiempo que los esquemas de diferencias finitas necesitan también se reduce a medida que la resolución aumenta (a medida que Δx y Δy disminuyen), lo cual significa que el modelo debe encargarse de más pasos de pronóstico intermedios para producir un pronóstico de la misma duración.
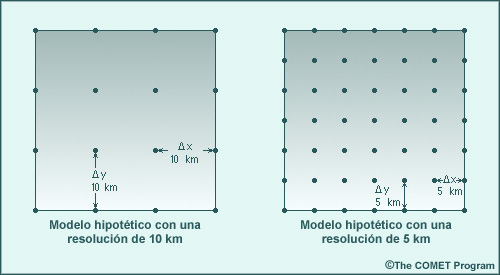
*Paso de tiempo
La relación que gobierna el intervalo de tiempo entre los pasos intermedios de pronóstico está dada por la ecuación de intervalo de tiempo que se muestra en la parte superior de la figura. La ecuación establece que el intervalo de tiempo (Δt) entre pronósticos intermedios debe ser menor que el tiempo que tarda la onda más rápida en el modelo (con velocidad c) en cruzar la distancia Δx. Esta restricción tiene una base física sencilla, ya que es preciso observar una parcela en movimiento con suficiente frecuencia como para poder seguir su trayectoria. La ecuación del intervalo de tiempo calcula el intervalo máximo entre los pasos de pronóstico intermedios para la resolución dada. Al aumentar la resolución es preciso reducir el intervalo de tiempo.
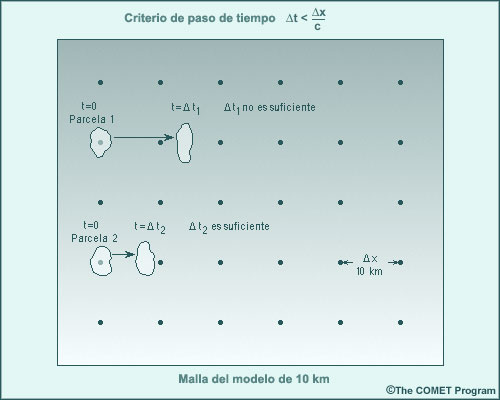
En la figura, el intervalo de tiempo no es suficientemente corto para la parcela 1, ya que la distancia que ha viajado es mayor que la distancia entre los puntos de malla del modelo (Δx) en un intervalo de tiempo (Δt1). Esto causa problemas (ruido) en la solución del modelo. El intervalo de tiempo (Δt2) es suficiente para la parcela 2, porque ha viajado una distancia menor que Δx.
En realidad, los modelos de PNT suelen utilizar intervalos de tiempo mucho menores a los indicados por esta ecuación. Esto se debe a la inestabilidad de los métodos numéricos y al uso de esquemas parametrización de elementos físicos que requieren intervalos de tiempo cortos para simular adecuadamente los procesos de pequeña escala.
*Ej. de paso de tiempo

Veamos un ejemplo de un modelo hipotético con un valor de Δx de 10 km. Aunque podríamos suponer que un intervalo de tiempo de una hora sería suficiente para pronosticar los movimientos de escala sinóptica, el modelo genera ondas con velocidades de propagación de más de 100 m/s respecto del viento, el cual puede alcanzar los 100 m/s en el centro del chorro. Por eso necesitamos considerar la velocidad de la onda más rápida en el modelo, por lo menos 200 m/s. Utilizando este valor para c obtenemos:

¡El intervalo de tiempo debería ser inferior a 50 segundos! El uso de intervalos de tiempo mayores puede producir rápidamente errores grandes en los campos de pronóstico y el «ruido» generado puede contaminar la salida del modelo.
*Ejercicio
Pregunta
¿Qué intervalo de tiempo y cuánta potencia de cómputo adicional se necesita para aumentar a 5 km la resolución del modelo utilizado en la página anterior? Utilice la relación del intervalo de tiempo proporcionada en la parte superior del gráfico para seleccionar las opciones correctas a continuación.
Si aumentamos la resolución a 5 km, el número de puntos de malla en cada nivel horizontal cuadruplica. El intervalo de tiempo necesario sería de 25 segundos, lo cual implica duplicar el número de pasos intermedios para generar el mismo pronóstico.
Por lo tanto, cada vez que se reduce a la mitad la distancia horizontal entre los puntos de malla de un modelo, ejecutar un pronóstico lleva ocho veces tanto tiempo [por ejemplo: (cuatro veces tantos puntos de malla) x (dos veces tantos intervalos de tiempo)]. Este cálculo supone que la resolución vertical y el dominio horizontal se mantienen iguales. Si además se duplica la resolución vertical, los requisitos computacionales se incrementarían 16 veces. Para poner esto en perspectiva, considere que si se duplica en todas las direcciones la resolución un modelo regional que tarda una hora en producir un pronóstico de 48 horas, ¡tardará 16 horas producir el mismo pronóstico!
Los centros de operaciones deben decidir qué resolución máxima del modelo permite finalizar la ejecución de un ciclo de pronóstico en determinado período, tomando en cuenta cuándo deben entregar la guía del modelo para cumplir con las necesidades de operaciones y la velocidad de los equipos informáticos que tienen a su disposición. Típicamente, los centros que utilizan modelos numérico aumentan considerablemente la resolución de los modelos solo después de haber adquirido equipos más potentes.
Además de la resolución, la física del modelo (especialmente los procesos de radiación, nubes y precipitación) también requieren mucha potencia de cálculo, y la asimilación de datos más aún. Pero dado que una representación más realista de los procesos físicos y mejores sistemas de asimilación de datos pueden producir pronósticos mucho mejores, los centros de modelado se ven obligados a aceptar un compromiso entre el uso de resoluciones más altas, sistemas de asimilación de datos más avanzados y mejores descripciones de los procesos físicos.
Resolución de estructuras
Definición de estructura
Normalmente se necesitan al menos cinco puntos de malla para definir un fenómeno atmosférico en un modelo de malla. Incluso en un pronóstico a corto plazo, la longitud de onda del fenómeno de menor escala que se puede conservar abarca entre cinco y siete puntos de malla. Para poder conservarse en pronósticos de uno o dos días, los fenómenos normalmente deben tener longitudes de onda mayores y abarcar ocho o diez puntos de malla.
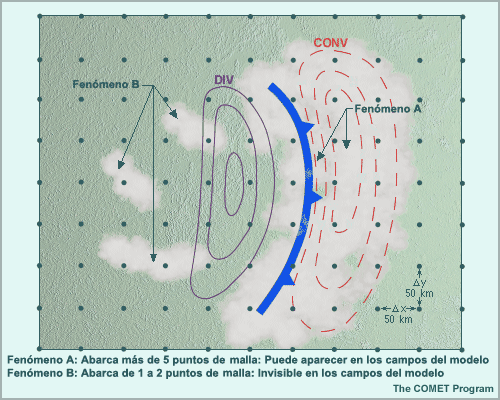
En este ejemplo de la convergencia/divergencia asociada con un frente frío, no cabe esperar que un modelo de malla con resolución de 50 km pueda resolver los fenómenos más pequeños (fenómenos B). El fenómeno frontal más grande, es decir, la región de convergencia asociada y la masa nubosa (fenómeno A), sí aparecerán en los campos del modelo. Aunque el modelo podría percibir los fenómenos atmosféricos de menos de 250 km de extensión y mayores que 50 km, no podrá resolverlos adecuadamente, lo cual producirá errores en la descripción de las características del fenómeno generada por el modelo.
Note que incluso si un fenómeno cumple con el criterio de tamaño resoluble, su orientación y yuxtaposición dentro de la malla del modelo puede aún causar una representación inadecuada.
Pregunta sobre la resolución
Pregunta
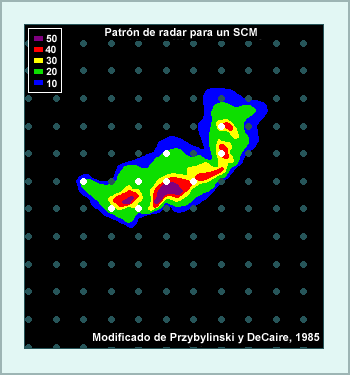
Supongamos que usted está trabajando con un modelo hipotético con una resolución de 30 km, y que un sistema convectivo de mesoescala (SCM) abarca un área definida por ocho o diez puntos de malla (>3000 km2). ¿En qué medida y con qué detalle debería el modelo poder resolver los procesos físicos y microfísicos asociados con el SCM? Escriba su respuesta en el espacio siguiente.
Comentario
Aun cuando un fenómeno atmosférico abarca un área definida por ocho o diez puntos de malla, a menudo el modelo no puede resolver todos los procesos físicos y microfísicos que produce el fenómeno. En el ejemplo, la distancia entre puntos de malla de un modelo de 30 km no permite resolver bien las corrientes ascendentes y descendentes ni los demás procesos de precipitación internos como para pronosticar la evolución del sistema, ya que la escala de estas estructuras es mucho más pequeña. Es posible que inicialmente el modelo resuelva el fenómeno, pero puede perderlo a lo largo del período de pronóstico si no se pueden definir los procesos físicos necesarios para mantenerlo o desarrollarlo.

La convección y los otros procesos de precipitación ocurren a escalas más pequeñas de las que la mayoría de los modelos operativos pueden resolver. Estos procesos se deben parametrizar para simular sus efectos en el ambiente de escala más grande y su impacto en los pronósticos a plazo más largo. Las parametrizaciones son particularmente importantes cuando el modelo no puede resolver una estructura pero puede predecir correctamente las condiciones atmosféricas de gran escala que conducen a su desarrollo.
El caso del SCM es un buen ejemplo, porque el modelo utiliza un esquema de parametrización convectiva para simular los efectos de los procesos convectivos en el ambiente de gran escala. El esquema se puede activar cuando el modelo pronostica condiciones atmosféricas favorables para la convección.
Las parametrizaciones se utilizan de muchas formas en la predicción numérica del tiempo. Sin embargo, si un modelo no puede describir un fenómeno o no pronostica bien las condiciones de su desarrollo, no se invocará la parametrización apropiada (esquema convectivo).
Ejemplo de gradientes
Como ilustra esta figura, la resolución del modelo también limita la intensidad de un gradiente. Dado que la acumulación del gradiente de temperatura justo detrás de un frente frío intenso es una estructura de pequeña escala, el modelo solo puede capturar el patrón de gran escala alrededor del frente. De forma análoga, los modelos operativos de resolución más alta apenas logran resolver la pared del ojo de un huracán, el lugar donde se pronostican los vientos más fuertes y un elemento esencial de la circulación vertical que sostiene la tormenta. Aunque es probable que se detecten las estructuras atmosféricas poco definidas, el modelo aumentará su tamaño y reducirá el fuerte gradiente de intensidad, produciendo una representación demasiado débil, mal ubicada, con detalles de evolución inexactos.
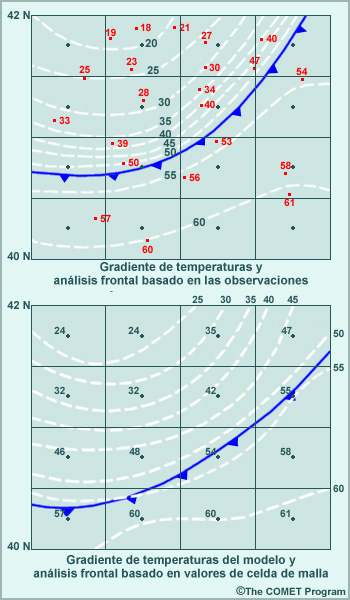
Además, puede producirse retroalimentación en los fenómenos que el modelo trata de simular pero no puede resolver. Por ejemplo, si se producen velocidades de calentamiento representativas de la convección, pero sobre una celda grande, la presión superficial del modelo puede bajar más de lo que lo sería el caso si el calentamiento solo ocurriera en la escala convectiva. A su vez, esto causa más convergencia de bajo nivel, lo cual aumenta las velocidades de calentamiento convectivas y causa una mayor reducción de la presión. Encontrará una explicación adicional sobre los ciclos de retroalimentación de la precipitación en la sección sobre procesos de precipitación del módulo ¿Cómo producen los modelos la precipitación y las nubes?.
Estructuras en análisis
La relación entre el tamaño del fenómeno atmosférico a pronosticar y la distancia entre puntos de malla en un modelo es crítica. Los siguientes ejercicios le permitirán comprobarlo.
Ejercicio 1: Condiciones iniciales del modelo
En este ejercicio escogerá una estructura o condición atmosférica, examinará la forma en que una onda la describe en un modelo de malla con una resolución de 20 km y comparará el modelo con las representaciones reales de la onda inicial y la advección de la onda. Muchas estructuras atmosféricas reales son asimétricas (como la convección, que produce corrientes ascendentes estrechas y una zona de descenso por compensación ancha), tienen bordes bien definidos (como las cuñas o franjas secas) o son principalmente perturbaciones de un solo signo (como las temperaturas superficiales asociadas con las islas de calor urbano). Sin embargo, siempre rigen los mismos principios relacionados con el grado de exactitud de representación y conservación del fenómeno en un pronóstico.
A medida que escoja y estudie cada fenómeno atmosférico, considere estas preguntas:
- ¿Cuántos puntos de malla abarca la onda?
- ¿Se puede reconocer una perturbación ondulatoria en la representación de malla?
- ¿El modelo representa bien la amplitud?
- Si viera esa estructura atmosférica en una secuencia de imágenes de satélite o de radar (representada por la línea roja) y en los campos iniciales del modelo (representados por la línea amarilla), ¿cómo evaluaría las condiciones iniciales del modelo?
- Suponiendo que la estructura atmosférica no cambia, sino que simplemente es transportada por un flujo medio perfectamente pronosticado, ¿cómo debería el modelo manejar el pronóstico de esta estructura?
En cada ejemplo, la estructura inicial completa del tiempo se representa como una onda periódica continua (curva roja) basada en la malla de 20 km del modelo. La forma en que el modelo representa el fenómeno atmosférico descrito por la curva roja uniforme se representa por medio de escalones azules. Dichos escalones azules representan el promedio de la curva uniforme real en cada celda de la malla. Los rombos azules indican los puntos de malla localizados en el centro de cada celda. La representación de los datos una vez procesados por el modelo de malla se vería como la línea amarilla que conecta los valores de puntos de malla, como si los datos correctos estuvieran localizados en el centro de la celda de malla.
Recuerde que los valores de los puntos de malla representan el promedio de la celda entera. En estos ejemplos, los valores iniciales de los puntos de malla son exactamente iguales al promedio de la curva roja de datos sobre la correspondiente celda azul. Todas las deficiencias en la representación son producto de las limitaciones impuestas por la resolución.
Fenómenos meteorológicos
~40 km
Smog urbano (longitud de onda ~40 km): Sólo dos puntos de malla del modelo describen la onda que representa el smog urbano. Aunque esta condición claramente existe, su forma y variaciones no están bien representadas. Aun antes del comienzo del pronóstico, la representación del modelo de este fenómeno atmosférico ha perdido alrededor del 25 % de su amplitud. Mucho del gradiente se pierde cerca de los picos de la onda y mucho más en los bordes de la misma. Esta estructura de pequeña escala apenas se capta en las condiciones iniciales del modelo.
~80 km
Lluvia o banda de nieve frontal (longitud de onda ~80 km): Cuatro puntos de malla del modelo describen la onda que representa la banda de lluvia o nieve frontal. Aunque la presencia de la estructura es obvia, la forma está mal representada. Si esta fuera una banda de lluvia frontal, el área de nubes y lluvia y la zona seca entre las bandas se podrían reconocer, pero se perdería la intensidad máxima. La estructura existe claramente en las condiciones iniciales del modelo, pero los detalles se han suavizado considerablemente. Esto afectará el pronóstico.
~140 km
Vórtice convectivo de mesoescala creado por un complejo convectivo de mesoescala (longitud de onda ~140 km): Siete puntos de malla del modelo describen la onda que representa el vórtice convectivo de mesoescala. La estructura se puede reconocer y tanto la amplitud como los gradientes parecen bien resueltos. Este parece un buen estado inicial. Sin embargo, siguen siendo inadecuados los cálculos de los campos de gradientes, como la vorticidad, que utilizan información de los puntos de malla a ambos lados de un lugar particular. Por ejemplo, la vorticidad en el tercer punto de malla se calcula utilizando los vientos en el segundo y el cuarto punto de malla. Viendo la representación, se observa que el campo de gradiente calculado (representado por la línea verde entre los puntos de malla 2 y 4) no calzará exactamente con las condiciones reales, aunque los gradientes máximos y la forma en general se ven bien. En el caso de un vórtice de mesoescala, si se utilizan datos de vientos de alta resolución en el sistema de asimilación de datos, la vorticidad máxima puede ser correcta, pero la distribución, especialmente cerca de los bordes del vórtice, puede no estar tan bien representada.
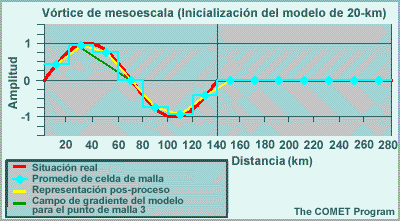
~200 km
Penacho de humedad alargado o franja seca en imágenes de vapor de agua (longitud de onda ~200 km): Diez puntos de malla del modelo describen la onda que representa el penacho de humedad. La representación de la onda de los puntos de malla se ve realmente como una onda y coincide en todo aspecto, inclusive el cálculo de los gradientes es bastante cercano a las condiciones reales. Los penachos de humedad y las franjas secas suelen ser lo suficientemente grandes para que un modelo de resolución de 20 km pueda resolverlos bien. El pronóstico debería ser bueno porque la estructura aparece bien resuelta y bien inicializada.
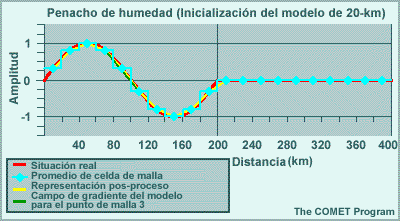
~400 km
Onda corta en la troposfera media montada sobre flujo rápido alrededor de una vaguada pronunciada (longitud de onda ~400 km): Veinte puntos de malla del modelo describen la onda que representa la onda corta. La representación del modelo de esta onda corta en la troposfera media es casi idéntica a los datos.
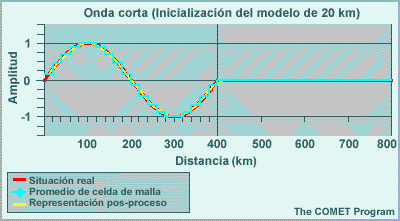
Estructuras en pronóstico
Ejercicio 2: Pronóstico del modelo
En las siguientes animaciones, las características atmosféricas del ejercicio de la página anterior se desplazarán hacia la derecha a razón de una longitud de onda a una velocidad constante únicamente por advección. Las características no experimentarán desarrollo dinámico ni amplificación.
Cada animación compara el pronóstico del modelo para una estructura y el movimiento real de la onda. La curva roja muestra el desplazamiento de la estructura hacia la derecha. Las celdas azules muestran el pronóstico del modelo. La línea amarilla representa los campos de salida posprocesados en la malla del modelo. La salida se muestra para diez períodos de pronóstico separados por intervalos aproximados de 17 minutos, hasta casi tres horas. El dominio real de cálculo del pronóstico es más grande que la región de salida que se muestra en las animaciones, de modo que las condiciones de frontera no son una fuente de error importante en estos cálculos simples. Sin embargo, al preparar un verdadero pronóstico del tiempo, es importante considerar los errores asociados con las condiciones de frontera.
A medida que examine cada animación, considere estas preguntas:
- ¿Se conserva la forma la onda?
- ¿Se mueve la onda la distancia correcta?
- ¿Qué sugiere esto sobre la capacidad del modelo de malla de pronosticar este fenómeno meteorológico?
Fenómenos meteorológicos
~40 km
Smog urbano (4 m/s): Con solo dos puntos que definen el smog urbano, el modelo no puede pronosticar esta característica atmosférica. Si recordamos la ecuación de diferencias finitas, la evolución temporal pronosticada depende de multiplicar la velocidad de la advección por el gradiente. Debido a que el gradiente en las celdas de la malla es una aproximación obtenida por medio de la diferencia entre los valores de las celdas vecinas a ambos lados, los gradientes en este ejemplo son casi cero en tres de los puntos que se muestran. Por lo tanto, el modelo no puede resolver la advección del smog en la dirección del viento. Los fenómenos de esta escala pueden introducir ruido en el campo de pronóstico del modelo. El pronóstico será mejor si omitimos aquellos fenómenos cuya longitud abarca dos espacios en la malla del modelo. Vea como mejora el pronóstico en el caso de estructuras de mayor escala.
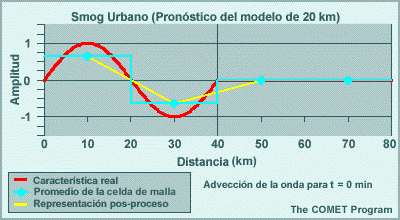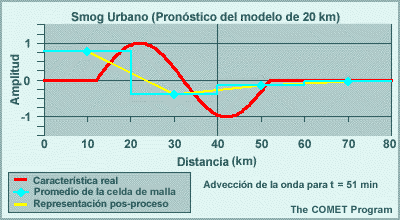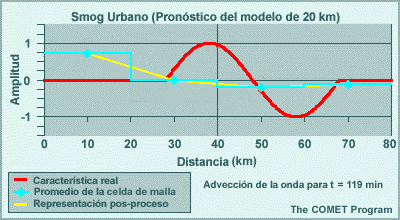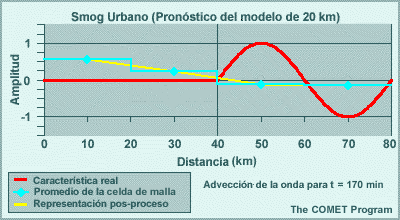
~80 km
Banda de precipitación (8 m/s): Con cuatro puntos del modelo de malla para definirla, la existencia de la banda de precipitación es reconocible, pero la solución numérica sufre de un considerable atraso de fase y un ensanchamiento de la longitud de onda. El extremo del flujo corriente abajo pierde amplitud mientras que el extremo del flujo corriente arriba oscila aún después de que la onda ha pasado. Aunque estas características variarán entre un esquema de diferenciación numérica a otro, por lo general el pronóstico de movimiento de un fenómeno atmosférico con una escala de cuatro espacios de malla será lento y su estructura no se pronosticará correctamente aun cuando parezca estar bien al inicio del pronóstico. Vea como mejora el pronóstico en el caso de estructuras de mayor escala.
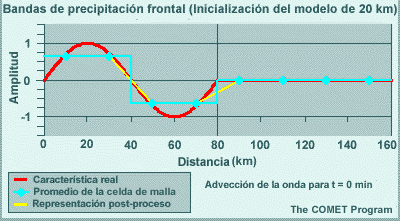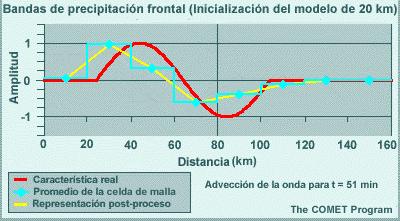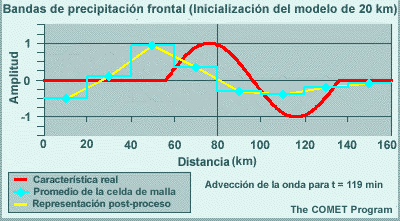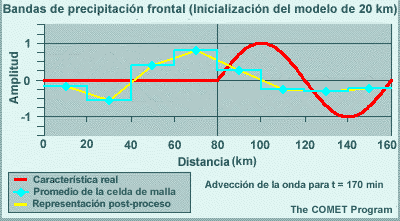
~140 km
Vórtice convectivo de mesoescala (14 m/s): La mitad del vórtice corriente arriba retiene su amplitud mientras las aproximaciones numéricas erosionan la mitad corriente abajo hasta que pierde la mitad de su amplitud original en solo tres horas. Además, el movimiento pronosticado es un poco lento. Aunque este resultado podría considerarse aceptable para un pronóstico de 24 horas, perder esa cantidad de la señal en tres horas no lo es. Existen técnicas numéricas en algunos modelos de pronóstico que pueden dar mejores resultados. Sin embargo, en términos generales las estructuras que abarcan siete espacios de malla no se pronosticarán tan bien como podría anticiparse, pese a que las observaciones se comparan favorablemente con los campos iniciales. Vea como mejora el pronóstico en el caso de estructuras de mayor escala.
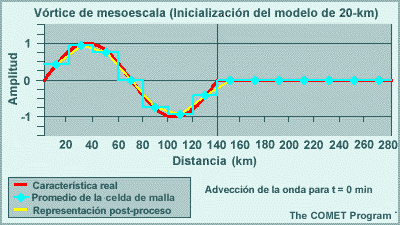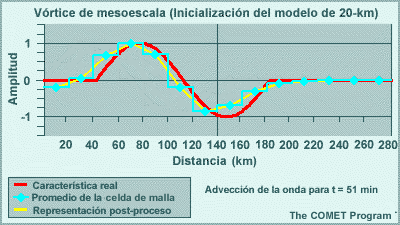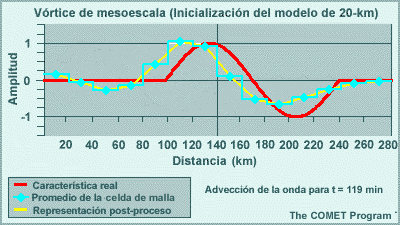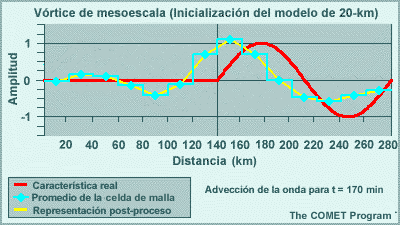
~200 km
Penacho de humedad o franja seca (20 m/s): En este ejemplo de resolución de 20 km, la bien definida lengua de aire húmedo o seco de escala subsinóptica se pronostica con exactitud. Sin embargo, todavía hay un retraso en el movimiento del modelo y el gradiente sobre el cuarto de longitud de onda corriente arriba ha perdido definición. Una estructura atmosférica con una escala del orden de 10 espacios de malla se pronosticará bien, pero existirá siempre un poco de error en algunos detalles. Compare estos errores con la cantidad de degradación en las estructuras de menor escala antes descritas.
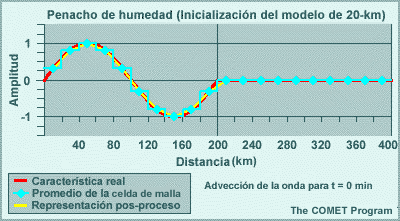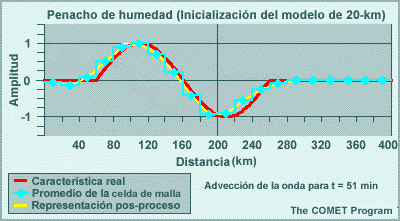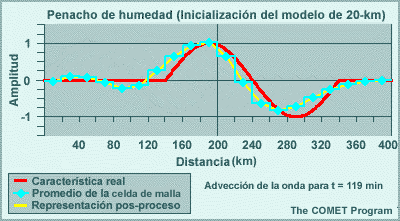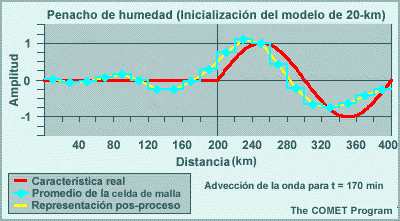
~400 km
Onda corta en la troposfera media (40 m/s): Gracias a los 20 puntos de malla que definen la onda corta, el modelo puede dar un tratamiento casi perfecto de la onda. La amplitud permanece prácticamente correcta tanto para el máximo como el mínimo, la fase es casi correcta y los gradientes sobre todas las porciones de la onda coinciden bastante con los valores exactos. Compare el pronóstico del modelo de esta estructura con los pronósticos de los fenómenos que abarcan menos puntos de malla para comprender la necesidad de mejorar la resolución en los modelos.
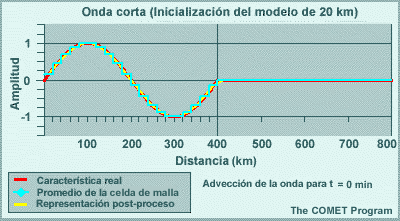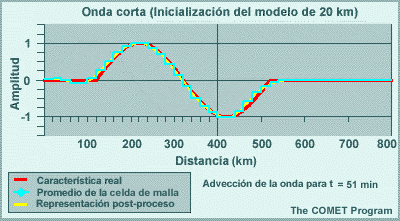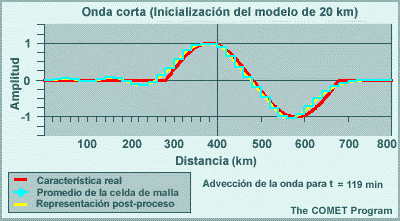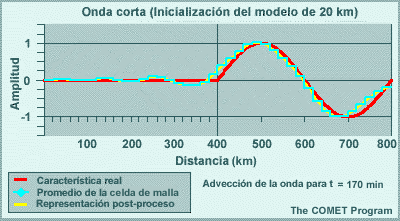
Discusión general: Al examinar los fenómenos meteorológicos pronosticados por un modelo, es preciso considerar:
- cuántos puntos de malla abarca la el fenómeno;
- la duración del pronóstico;
- si la estructura puede ser completamente espuria porque el modelo no puede pronosticar fenómenos de ese tamaño;
- si la existencia del fenómeno puede ser realista, pero su forma y estructura (gradientes) están representados de forma muy pobre y el movimiento pronosticado es muy lento;
- que las estructuras que solo abarcan pocos puntos de malla y están relacionadas con esfuerzos persistentes conocidos, como las circulaciones orográficas o costeras, estarán siempre sujetas a estos esfuerzos, aun cuando la resolución de su estructura es pobre. Su efecto se puede propagar demasiado en el modelo.
El intervalo de paso de tiempo también contribuye al error de truncamiento: mientras mayor sea el intervalo de paso de tiempo, mayor será el error introducido a través de la aproximación de diferencias finitas.
Preguntas sobre la resolución horizontal
Ejercicio: pronóstico extendido
Pregunta
¿Cuáles de los fenómenos atmosféricos indicados a continuación puede resolver bien un modelo con una resolución de 35 km o un modelo espectral T360 utilizado para generar un pronóstico extendido? Para cada fenómeno atmosférico indicado a continuación, decida si se puede resolver bien (Sí/No/Limitado). Use el cuadro de selección para elegir la mejor respuesta para el enunciado.
Comentario
Algunos de estos fenómenos se pueden describir mediante un modelo de 35 km, en el cual cada celda de la malla tiene un área de 1225 km2. Sin embargo, la mayoría no serán tan pronunciados en la realidad o se perderán detalles importantes. Los problemas específicos de cada fenómeno se explican a continuación.
Se pueden resolver
Invasión de aire ártico al este de las Montañas Rocosas y empozamiento de aire frío: Ambos son inducidos por topografía de escala suficiente para que este modelo los pueda resolver. Deberían estar bien resueltos sobre las llanuras adyacentes y al este de las montañas. Sin embargo, la penetración del aire frío en terreno complejo no se resolverá y como muchos valles (como el de Shenandoah) ni siquiera forman parte de la topografía del modelo, este no puede mostrar el aire frío atrapado en el valle. La resolución vertical y la formulación de la coordenada vertical son aspectos críticos para resolver la topografía, el gradiente de presión y la estabilidad cerca de la superficie, todos elementos que afectan los procesos de erosión de las situaciones de empozamiento o estancamiento de aire frío. Además, la física del modelo juega un papel importante en determinar el momento de erosión de una situación de estancamiento de aire frío, especialmente la parametrización de la turbulencia en la capa límite.
Frente en altura y frente sinóptico de superficie: El frente en altura es lo suficientemente ancho como para que el modelo lo describa bien. Todavía se necesita una resolución vertical aceptable para resolverlo, pero lo normal es que un modelo de 35 km cuente con suficientes niveles verticales. El frente sinóptico de superficie puede tener gradientes en su frontera de avance demasiado pronunciados para el modelo los pueda resolver, pero las características generales del frente y su ubicación deberían estar bien.
Se pueden resolver en forma limitada
Banda de nieve dentro de un ciclón en la costa este: Normalmente, esta estructura es lo suficientemente larga, pero demasiado estrecha para que un modelo de 35 km logre capturarla. El modelo puede mostrar una intensidad de precipitación local mayor a la realidad. Si el modelo no puede reproducir la banda de nieve, se pueden utilizar los diagnósticos del modelo, como la inestabilidad simétrica condicional y la frontogénesis, para inferir la probabilidad de su ocurrencia.
Máximos/Mínimos de precipitación inducidos por el terreno: Tanto el tamaño del fenómeno como el terreno influyen en la capacidad del modelo para resolver estos patrones. Los patrones de precipitación inducida por el terreno tienden a ser bastante pequeños e intrincados, y siguen de cerca las características del terreno. El modelo de 35 km de resolución debería ser lo suficientemente bueno como para evitar un desplazamiento importante en el pronóstico de precipitación fuerte. Sin embargo, es probable que los picos se subestimen y que no se pueda indicar puntualmente los máximos de precipitación.
Frente costero: Tanto el tamaño del frente costero como la descripción del terreno en el modelo permiten que el modelo describa este fenómeno. Aunque un frente costero puede extenderse por cientos de kilómetros a lo largo de la costa, es delgado. La caracterización del modelo de la línea costera tiene influye en la ubicación y la intensidad del frente costero en el modelo, y la frontera misma puede ser muy abrupta para que se represente apropiadamente en una malla de 35 km.
Circulación de brisa marina: La circulación vertical de brisa marina es más pequeña que la distancia entre puntos de malla del modelo. El modelo tratará de crear una brisa marina a la menor escala posible, de manera que será visible, pero se extenderá demasiado tierra adentro.
Sistema convectivo de mesoescala: A veces el modelo puede pronosticar un área de precipitación convectiva donde se puede desarrollar un SCM. Sin la física ni la resolución para simular los procesos internos de un SCM, el modelo no puede simular apropiadamente la evolución y la propagación del SCM ni los efectos corriente abajo.
Huracán: Los huracanes pueden cubrir desde decenas hasta varios cientos de miles de kilómetros cuadrados, de forma que su extensión es más que suficiente para que un modelo de 35 km pueda resolverlos. Sin embargo, debido a los intensos gradientes de presión, los movimientos verticales y otros procesos dinámicos y termodinámicos que ocurren a escalas relativamente más pequeñas, el huracán del modelo probablemente será muy débil y algunas veces estará mal ubicado.
No se pueden resolver
Tormenta de viento de ladera descendente: No se puede resolver bien debido tanto a consideraciones de tamaño como de terreno. Depende de la componente de viento que atraviesa la montaña y el perfil de estabilidad de la atmósfera. La fuerte onda de montaña que causa la tormenta de viento es demasiado localizada como para que un modelo de 35 km la pueda detectar.
Frontera de flujo saliente: La zona delgada que normalmente define las fronteras de flujo saliente y los procesos internos que ocurren dentro de la célula de la tormenta que las produce no se pueden resolver adecuadamente en un modelo de 35 km.
Ejercicio de mesoescala
Pregunta
¿Cuáles de los siguientes fenómenos atmosféricos se pueden resolver adecuadamente con un modelo de mesoescala de una resolución de 10 km? Para cada fenómeno atmosférico indicado a continuación, decida si se puede resolver bien (Sí/No/Limitado). Use el cuadro de selección para elegir la mejor respuesta para el enunciado.
Comentario
Todos estos fenómenos se pueden describir en cierta medida con un modelo de 10 km, en el cual cada celda de la malla tiene un área de 100 km2. Sin embargo, algunos no serán tan pronunciados como en la realidad o perderán detalles importantes, incluso a esta resolución. En el caso de muchos fenómenos, la física del modelo y las condiciones iniciales limitan la exactitud del pronóstico más que la resolución. Los problemas específicos de cada fenómeno se explican a continuación.
Se pueden resolver
Invasión de aire ártico al este de las Montañas Rocosas y empozamiento de aire frío: Ambos son inducidos por topografía de escala suficiente para que este modelo los pueda resolver. Deberían estar bien resueltos sobre las llanuras adyacentes y al este de las montañas. Sin embargo, la penetración del aire frío en terreno complejo no se resolverá bien. Por ejemplo, un modelo con una resolución de 10 km incluye valles del tamaño del Shenandoah, que abarca un área de casi 300 km, pero se trata de una representación aproximada. Además, independientemente de la resolución, la física del modelo juega un rol clave en el pronóstico de la erosión de un evento de empozamiento de aire frío.
Frente en altura y frente sinóptico de superficie: El frente en altura es lo suficientemente ancho como para que el modelo lo describa bien. Todavía se necesita una resolución vertical aceptable para resolverlo, pero lo normal es que un modelo de 10 km cuente con suficientes niveles verticales. Aunque el frente sinóptico de superficie puede exhibir un cambio en la dirección del viento más fuerte de lo que el modelo puede resolver, debería ser posible resolver el patrón del gradiente de temperatura de cualquier frente menos los más extremos.
Frente costero: Con una malla de 10 km y dadas condiciones iniciales y una física adecuadas, el modelo debería poder resolver la forma del litoral y la topografía lo suficientemente bien como para generar un frente costero cerca del lugar correcto con propiedades de masa de aire similares a las observadas en ambos lados del frente.
Se pueden resolver en forma limitada
Banda de nieve dentro de un ciclón en la costa este: Es posible resolver una única banda de nieve si es ancha, como de 50 km de anchura. Con frecuencia, la longitud de onda entre el centro de una banda de nieve y el centro de la próxima es menor de 40 km. Esa estructura es demasiado pequeña para que un modelo pueda detectarla a una resolución de 10 km. En su lugar, el modelo genera una sola banda de precipitación muy intensa.
Máximos/Mínimos de precipitación inducidos por el terreno: Tanto el tamaño del fenómeno como el terreno influyen en la capacidad del modelo para resolver estos patrones. Los patrones de precipitación inducida por el terreno tienden a ser bastante pequeños e intrincados, y siguen de cerca las características del terreno. A una resolución de 10 km, el patrón general parecerá bueno, pero estará concentrado en una zona muy reducida, sin resolver la variación local.
Circulación de brisa marina: La circulación vertical de brisa marina es más pequeña que la distancia entre puntos de malla del modelo. El modelo tratará de crear una brisa marina a la menor escala posible, de manera que será visible y en una posición cercana a la realidad, pero el gradiente de temperatura y los vientos en la zona de avance serán demasiado débiles.
Sistema convectivo de mesoescala: El modelo puede resolver el sistema convectivo de mesoescala como entidad y distinguir la zona de nubes estratiformes y la región de convección del sistema. También puede producir un flujo frío saliente y resolver algunos aspectos de la circulación estratiforme, incluido el vórtice. No obstante, la física del modelo conduce a estructuras erróneas, como la generación del vórtice por motivos equivocados y en los niveles incorrectos, así como la propagación errónea. Los esquemas de parametrización de la convección tienen grandes problemas con el movimiento de los sistemas convectivos, mientras que con una parametrización subactiva de la convección el modelo ocasiona el crecimiento un cumulonimbo muy grande a escala de malla que produce demasiada precipitación. Además, es probable que el modelo produzca errores de momento y posición en lo referente a la predicción del inicio del sistema, y en su trayectoria.
Huracán: Los huracanes pueden cubrir desde decenas hasta varios cientos de miles de kilómetros cuadrados, de forma que su extensión es más que suficiente para que un modelo de 10 km pueda resolverlos. El modelo tratará de crear la pared del ojo, pero esta será casi tan delgada como en las observaciones y mal resuelta (demasiado débil), o bien será demasiado ancha. Debido al rol fundamental de la pared del ojo en la dinámica y termodinámica de los huracanes, la incapacidad de resolver la pared del ojo limita la capacidad del modelo de predecir la intensidad de la tormenta con exactitud; no obstante, dadas una física y condiciones iniciales adecuadas, el modelo debería producir un pronóstico útil de tendencias de trayectoria e intensidad.
Tormenta de viento de ladera descendente: Un modelo de 10 km cuenta con una resolución topográfica y dinámica suficientes como para crear una onda de montaña de gran amplitud con vientos intensos en los niveles bajos. Sin embargo, es posible que la onda aún no esté suficientemente definida en el modelo y los vientos pronosticados en niveles bajos no serán tan fuertes como los vientos máximos observados. Además, un modelo con una resolución de 10 km no puede resolver las variaciones de intensidad locales de un viento catabático.
Frontera de flujo saliente: Aunque un modelo con una resolución de 10 km puede generar un frente de racha y una frontera de corriente de salida, no es capaz de resolver los vientos más intensos cerca del borde del frente de racha y no puede resolver el rotor del viento. Los factores principales que limitan la predicción de la frontera de corriente de salida son los errores del modelo en el inicio de la convección y la propagación del sistema convectivo de mesoescala.
Ejercicio sobre un sistema convectivo
Pregunta
Las siguientes preguntas están relacionadas con un modelo de mesoescala con una resolución de 4 km. Escriba su respuesta en el espacio después de cada pregunta.
Comentario
a) Normalmente, los SCM son lo suficientemente grandes para que un modelo de 4 km los pueda resolver, aunque con limitaciones. Dado el número de puntos de malla cubiertos por el sistema, es probable que el modelo identifique correctamente la región de fuerte precipitación inicial asociada con el SCM. Sin embargo, los aspectos de momento de inicio y cantidad de precipitación son sensibles al método de asimilación de datos y a varias parametrizaciones físicas, incluida la microfísica.
b) La corriente de salida del SCM normalmente es producto de la acumulación de circulaciones de mesoescala, lo cual a veces incluye chorros entrantes posteriores. Un modelo de 4 km puede generar y resolver estas estructuras adecuadamente. El modelo puede generar una bolsa de aire frío razonablemente intensa, desplazarla hacia adelante y generar convección adicional en su borde. Sin embargo, aquí también los detalles son sensibles a la parametrización de microfísica y a otros parámetros físicos del modelo, lo cual puede impartir al pronóstico una trayectoria diferente de la que exhibe en la atmósfera real, pese a que la resolución del modelo es adecuada.
c) Las supercélulas grandes se pueden resolver de forma aproximada en un modelo de 4 km, pero sus subestructuras, como el mesociclón y la nube pared, no. Los núcleos de corrientes ascendentes de una tormenta multicelular ordinaria miden aproximadamente 1 km de ancho, y claramente son demasiado pequeños para que este modelo los pueda resolver. El modelo creará un núcleo de corriente ascendente de un diámetro de un par de puntos de malla, lo cual significa que las células pequeñas son excesivamente grandes. Típicamente, el modelo genera células que se desplazan hacia la derecha, células hendidas, células cuya columna de precipitación atraviesa la corriente ascendente y se disipan, y células de otros tipos, como en la realidad, y las genera en los mismos tipos de entornos que la naturaleza. Sin embargo, las condiciones iniciales no son casi nunca lo suficientemente exactas como para producir el inicio en el lugar y el momento correctos, y las células excesivamente grandes del modelo no interactúan de la misma forma que las células naturales, por lo que el modelo pronostica células en momentos y lugares incorrectos incluso cuando la organización de mesoescala, el modo convectivo, se predice bien.
Resumen
Este resumen presenta los puntos clave asociados con la resolución horizontal de los modelos de malla y los modelos espectrales.
Modelos de malla
- La resolución horizontal se define como la separación entre puntos de malla.
- Los fenómenos atmosféricos más pequeños que se pueden pronosticar con un modelo de malla deben tener longitudes de onda completas que cubran un mínimo de cinco a siete puntos de malla.
- Los recursos de cómputo limitan la separación mínima de los puntos de malla en un modelo, dado el gran aumento del tiempo de cómputo que requiere ejecutar los modelos de mayor resolución.
- La separación entre puntos de malla afecta la capacidad del modelo de representar el terreno, lo cual a su vez afecta la medida en que el modelo puede definir los fenómenos meteorológicos inducidos o afectados por el terreno.
Modelos espectrales
- La resolución horizontal es una función del número de onda (el número de ondas utilizadas para representar los datos).
- Cuanto mayor el número de ondas, tanto más fina la resolución.
- Mientras más ondas se utilicen para representar los datos, más potencia de cómputo se necesita para realizar los cálculos.
- La representación del terreno y los fenómenos atmosféricos asociados mejora cuando se aumenta el número de ondas.
La capacidad de un modelo de resolver un fenómeno atmosférico depende no solo de su resolución horizontal, sino también de su resolución vertical, el número de capas verticales y el paquete físico utilizado para definir una variedad de procesos atmosféricos y de superficie. Además, los modelos de área limitada se ven fuertemente limitados por sus condiciones de frontera.
Resolución vertical
Introducción
De forma análoga a la necesidad de contar con una resolución horizontal adecuada para describir diferentes fenómenos atmosféricos, los modelos numéricos de predicción del tiempo y los sistemas de análisis se deben diseñar con la resolución vertical adecuada para pronosticar la estructura vertical y los efectos de una variedad de eventos meteorológicos. Al igual que la malla o cuadrícula del modelo representa un promedio de las condiciones atmosféricas en cada celda de la malla, en sentido vertical el valor del modelo en determinado nivel de la malla representa las condiciones a lo largo de una capa. Tanto los modelos espectrales como los de malla representan la columna atmosférica en capas discretas.
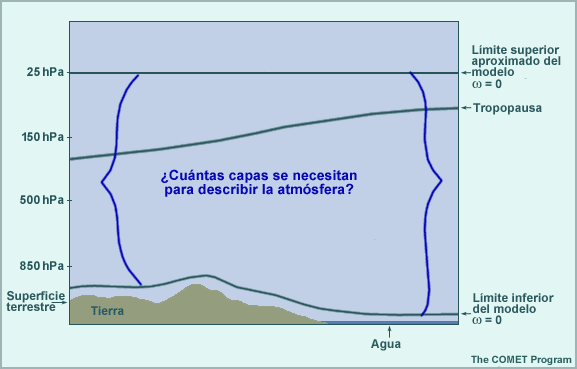
Estas son algunas de las estructuras clave que necesitan una resolución vertical adecuada:
- Fuertes inversiones térmicas cerca de la superficie y gradientes superadiabáticos que afectan los intercambios de calor, humedad y momento entre la atmósfera y la superficie y afectan en gran medida las predicciones de temperaturas y puntos de rocío a 2 metros y vientos a 10 metros
- La parte superior de la capa límite, que afecta el crecimiento de la capa límite y la mezcla entre la capa límite y la atmósfera libre.
- Zonas frontales inclinadas, donde los procesos
baroclínicos son importantes.
- La(s) tropopausa(s), que afecta(n) la dinámica e intensidad de los chorros y la estructura de las potenciales anomalías de vorticidad.
No se necesita una resolución vertical fina en la troposfera media a alta en condiciones tropicales y barotrópicas de verano, cuando la tropopausa está a gran altura. En su lugar, la concentración de una mayor cantidad de capas cerca del suelo permite capturar mejor los procesos de superficie que afectan el ciclo diurno, la inestabilidad convectiva y el forzamiento topográfico y costero de la convergencia que pueden profundizar la capa húmeda y desencadenar la convección.
Un modelo con asignaciones de capas verticales fijas debe encontrar el justo medio al asignar las capas verticales a las posiciones ideales para diferentes regímenes meteorológicos, como los trópicos y el invierno de latitudes medias. Con un sistema de coordenadas adaptable, como la coordenada isoentrópica, el modelo puede colocar los niveles donde más se necesitan para una serie de situaciones diferentes, sin necesitar tantos niveles que tarda más tiempo en ejecutar un ciclo.
Es interesante notar que la relación entre la resolución horizontal y la resolución vertical debe ser coherente con la pendiente del fenómeno atmosférico de interés. Si no se cuida este aspecto, los pronósticos de un modelo con resolución fina en una sola dimensión pueden resultar peores que los pronósticos de los modelos con menor resolución. La mayoría de los centros operativos usan muchas capas, más que suficientes para evitar este problema.
Distribución de las capas
*Modelo global
Las capas verticales rara vez se distribuyen uniformemente. A menudo, las limitaciones de los recursos computacionales nos obligan a concentrar la densidad de las capas verticales en ciertas regiones específicas con el fin de describir de la mejor forma posible las estructuras atmosféricas de interés para los problemas de escala global y de mediano alcance.
Pregunta
Si usted estuviera diseñando un modelo global, ¿dónde ubicaría la mayor concentración de capas verticales para generar pronósticos de 1 a 2 días? Use el cuadro de selección para elegir la mejor respuesta para el enunciado.
Comentario
Para capturar la evolución de los ciclones, anticiclones y frentes asociados a medida que se desplazan sobre la superficie terrestre, es importante resolver las estructuras de la corriente en chorro que impulsa la evolución de estos sistemas. Por consiguiente, se puede lograr una mejor descripción de la evolución de las estructuras atmosféricas en la escala global concentrando las capas en el nivel de la corriente en chorro. Para pronósticos a más largo plazo, sin embargo, el impacto de los procesos cerca de la superficie terrestre puede volverse dominante, lo cual requiere un aumento de resolución en la capa límite.
*Modelo de mesoescala
Si usted estuviera diseñando un modelo de mesoescala para pronosticar específicamente el inicio de la convección o nieve por efecto lago, ¿dónde concentraría las capas verticales del modelo? Use el cuadro de selección para elegir la mejor respuesta para el enunciado.
Comentario
Es necesaria una resolución detallada de la capa límite para describir adecuadamente los efectos de los procesos diurnos y de superficie en la estabilidad de la capa límite, por ejemplo:
- inestabilidad provocada por el calentamiento superficial;
- humectación provocada por la evapotranspiración de la vegetación;
- calentamiento y humectación a lo largo de los litorales;
- contacto con aguas cálidas.
Junto con una representación detallada de los regímenes de viento de bajo nivel y los contrastes de fricción entre agua y tierra, estos procesos son importantes en la creación de las condiciones de capa límite y el inicio de tormentas de nieve por efecto lago.
*Para ondas cortas de latitudes medias
Si usted estuviera diseñando un modelo para rastrear ondas cortas de latitudes medias y pronosticar eventos asociados de ciclogénesis y ondas frontales, ¿dónde concentraría sus capas verticales? Escoja todas las opciones pertinentes.
Comentario
Las respuestas más apropiadas son troposfera media (b) y nivel de la corriente en chorro (c). Aunque la capa límite es importante para la frontogénesis en superficie, el nivel de la corriente en chorro es importante para seguir las circulaciones directas e indirectas del chorro y sus efectos en la ciclogénesis que dirige los procesos frontales a lo largo de la atmósfera. Sin embargo, el conocimiento de las condiciones en el nivel de la corriente en chorro por sí solo no es suficiente. Con frecuencia, las ondas cortas en la troposfera media se pueden seguir por todo el globo y se ha demostrado que están asociadas con múltiples y distintos eventos de ciclogénesis (Sanders 1988). En muchos casos, el desarrollo de ciclones de latitudes medias parece ser más sensible a anomalías de vorticidad potencial en la troposfera media (incluyendo aquellas que se propagan hacia abajo desde la estratosfera) que aquellas en la baja y alta troposfera (Morgan, comunicación personal).
Asimilación de datos
Históricamente, la resolución de los modelos de PNT por encima de la tropopausa ha sido relativamente gruesa. Sin embargo, con la creciente necesidad de pronosticar las concentraciones de ozono, la extensión de los pronósticos de mediano a largo plazo y el desarrollo de técnicas avanzadas de asimilación de datos satelitales, la resolución en la estratosfera se ha vuelto un aspecto de creciente importancia.
En esquemas variacionales de asimilación de datos, las radiancias atmosféricas utilizadas para determinar la estructura vertical de la atmósfera dependen de pronósticos exactos de las concentraciones de los agentes que absorben radiaciones de onda corta y larga, como el ozono. Por ejemplo, el mayor impacto positivo de la utilización de datos satelitales en los pronósticos para el hemisferio norte se produjo al incluir la información de concentración de ozono en la estratosfera en el sistema de asimilación variacional. Esto es más importante para las zonas oceánicas que no cuentan con datos, como el Pacífico Norte (Derber y Wu 1998).
Ubicación óptima de las capas
La ubicación óptima de las capas depende del fenómeno de interés. Esto varía con la época del año y la región geográfica, así que cualquier parte de la atmósfera puede ser crítica en un momento dado:
- Capa límite: para capturar procesos diurnos e influencias superficiales
- Atmósfera libre en la troposfera: para pronosticar ondas cortas, corrientes en chorro, ciclones, ondas tropicales, etc.
- Estratosfera o más arriba: para pronósticos a largo plazo y asimilación de datos de satélite
Dado que un modelo operativo de PNT debe ser útil en diferentes épocas del año y regiones geográficas, cualquier parte de la atmósfera puede ser crítica en un momento dado, y habrá que decidir por un punto intermedio. Sin embargo, a medida que aumentan la resolución y el alcance de los pronósticos, la necesidad de contar con mejores modelos de calentamiento y fuentes de humedad en la superficie fomenta el incremento de la resolución en los niveles cercanos al suelo, tanto en la mesoescala como en la escala global.
*Modelos locales
Mientras que los modelos que se ejecutan en los centros meteorológicos nacionales tienen configuraciones predeterminadas para sus dominios y resoluciones horizontales y verticales, algunos modelos que se emplean a nivel local brindan al usuario la posibilidad de ajustar varios parámetros, incluyendo el número y la ubicación de los niveles verticales (y por lo tanto de las capas definidas por esos niveles).
Cuando se ajusta una configuración local, es importante considerar lo siguiente:
- Fenómenos de interés: Esto determina la resolución vertical necesaria en diferentes alturas.
- Variaciones en el espesor de las capas: El espesor entre las capas debería cambiar gradualmente.
- Recursos computacionales: El tiempo de ejecución del modelo limita el número de capas que se pueden utilizar.
- Resolución horizontal: Se debe mantener una relación coherente entre la resolución vertical y la resolución horizontal.
- Fuente de condiciones de frontera: Se debe guardar coherencia con el modelo que suple las condiciones de frontera.
- Intervalo de tiempo: Ciertas
restricciones
numéricas pueden exigir
intervalos de tiempo menores
si se utiliza una resolución vertical
más
fina, lo
cual afecta al tiempo de
ejecución del modelo.
Estas restricciones incluyen:
- La velocidad vertical máxima esperada en cualquier lugar y en cualquier momento del pronóstico.
- La velocidad de caída de hidrometeoros (si es pertinente) de manera que las partículas de precipitación no se salten una celda de la malla en un intervalo de tiempo.
- Esquemas numéricos para la advección vertical que requieren un espaciamiento relativamente uniforme de las capas verticales.
- Las técnicas utilizadas para manejar las ondas de sonido que se propagan verticalmente, en modelos compresibles o cuasi-compresibles, como RAMS y UW-NMS.
Siempre se requiere algún grado de investigación y experimentación a la hora de determinar las configuraciones más adecuadas para determinadas aplicaciones individuales del pronóstico.
Tipos de coordenadas y resolución vertical
La capacidad de un sistema de coordenadas verticales de representar las características atmosféricas en la vertical depende de las características de resolución vertical. Algunos sistemas incrementan inherentemente la resolución en ciertos lugares donde es deseable hacerlo, otros permiten ajustar fácilmente los niveles, mientras que otros no son muy adaptables o flexibles. Es importante entender cómo las características de resolución vertical de cada sistema de coordenadas influyen en la capacidad de un modelo dado de representar las estructuras meteorológicas.
También es importante recordar que en todos los sistemas de coordenadas verticales, el espesor de la capa debe cambiar gradualmente de una capa a la siguiente. De otra forma, los errores en los esquemas verticales de diferencias finitas del modelo, como los que se utilizan para calcular la advección del momento, calor y humedad en la vertical, se verán amplificados. Por lo tanto, dado que la resolución debe ser de unas cuantas decenas de metros cerca del suelo para describir apropiadamente una variedad de procesos superficiales, debe haber un gran número de niveles en la capa límite planetaria para que actúe como una zona de transición con respecto a la troposfera media, donde los niveles se encuentran más separados.
*Isoentrópica

Pregunta
Examine esta sección vertical de las superficies de coordenadas, luego describa los méritos del enfoque de coordenadas verticales isoentrópicas en lo que se refiere a la resolución vertical. Escriba su respuesta en el espacio siguiente.
Comentario
Las coordenadas isoentrópicas aumentan naturalmente la resolución vertical en las capas estables, como en los frentes y cerca de la tropopausa, y en otras regiones donde la temperatura potencial aumenta rápidamente con la altura. Debido a que a menudo en estas regiones existe una fuerte cortante vertical y horizontal del viento, la descripción y los pronósticos de estas estructuras mejoran con el aumento natural en la resolución que se crea al utilizar la temperatura potencial como la coordenada vertical. Sin embargo, como ya se señaló en la sección «Coordenadas verticales», las coordenadas isoentrópicas tienen deficiencias que las vuelven inutilizables cerca de la superficie de la Tierra.
En primer lugar, con frecuencia intersecan el suelo. Además, en regiones con capas límites bien mezcladas (superficies isoentrópicas muy espaciadas y casi verticales) el gradiente vertical de temperatura es casi adiabático y las superficies de temperatura potencial pueden volverse casi constantes con la altura. El gran espaciamiento vertical entre las superficies isoentrópicas reduce enormemente la capacidad del modelo de describir de forma adecuada los procesos de capa límite. Finalmente, el requisito de que la coordenada vertical de un modelo varíe monotónicamente con la altura impide utilizar las coordenadas isoentrópicas en situaciones donde existen gradientes verticales de temperatura superadiabáticos, como cerca de la superficie terrestre en períodos diurnos soleados.
*Isoentrópica-sigma

Pregunta
Examine esta sección vertical de las superficies de las coordenadas, luego describa los méritos del enfoque híbrido de coordenadas verticales isoentrópicas-sigma en lo que se refiere a la resolución vertical. Escriba su respuesta en el espacio siguiente.
Comentario
El enfoque híbrido combina las ventajas de dos sistemas de coordenadas. Cerca de la superficie, la coordenada vertical sigma permite obtener una resolución alta en la capa límite, aún sobre terreno complejo. Esto es útil para describir el efecto de los procesos diurnos y la influencia de la superficie en la capa límite planetaria. Dichos procesos afectan la temperatura y la humedad cerca de la superficie, las cuales, a su vez, determinan la estabilidad de la capa límite. Cabe recordar, sin embargo, debido al uso de la coordenada sigma en la capa límite los modelos isoentrópico-sigma son susceptibles de algunas de las mismas limitaciones de la capa límite que ya señalamos para los modelos sigma.
En altura, la naturaleza adaptable de las coordenadas verticales isoentrópicas brinda una resolución vertical que aumenta naturalmente en las regiones baroclínicas de importancia, como las zonas frontales y la tropopausa. Para hacerlo, el modelo debe contener un número relativamente alto de niveles isoentrópicos, distribuidos de manera tal que la diferencia de temperatura potencial entre los niveles en la troposfera sea considerablemente menor que en la estratosfera, la cual es estáticamente más estable.
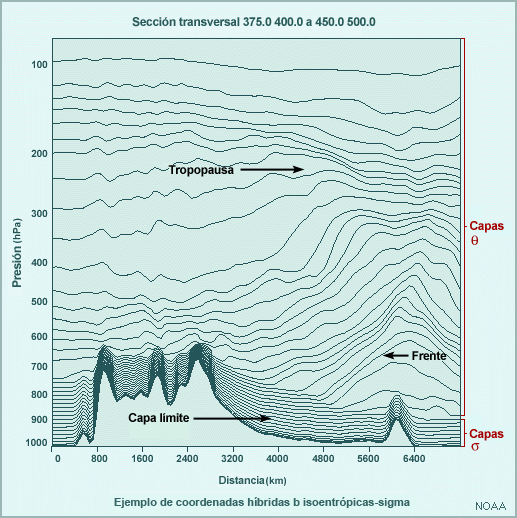
Isobárica-sigma
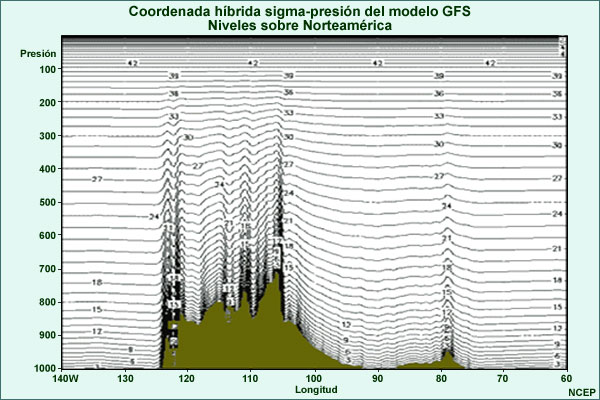
Pregunta
Examine esta sección vertical de las superficies de coordenadas, luego describa las ventajas del enfoque híbrido de coordenadas verticales isobáricas-sigma. Escriba su respuesta en el espacio siguiente.
Comentario
El enfoque híbrido isobárico-sigma conserva la ventaja de alta resolución en la capa límite de la coordenada sigma, incluso sobre terreno complejo. Esto es útil para describir el efecto de los procesos diurnos y la influencia de la superficie en la capa límite planetaria. Dichos procesos afectan la temperatura y la humedad cerca de la superficie y, a su vez, estos factores determinan la estabilidad de la capa límite.
En altura, la coordenada isobárica es relativamente plana y ofrece propiedades numéricas robustas. Sin embargo, el beneficio principal no se percibe en términos de la resolución vertical, sino en la asimilación de las observaciones de radiancia de los satélites. Cada canal satelital mide la radiancia en una banda espectral muy estrecha a la cual se asigna una función de ponderación que es una función conocida de la presión. El procesamiento de estos datos con los modelos de transferencia radiativa es mucho más eficiente y exacto cuando el modelo usa coordenadas isobáricas. Además, la asimilación óptima de las observaciones de radiancia obtenidas por los satélites requiere muchas capas en la estratosfera.
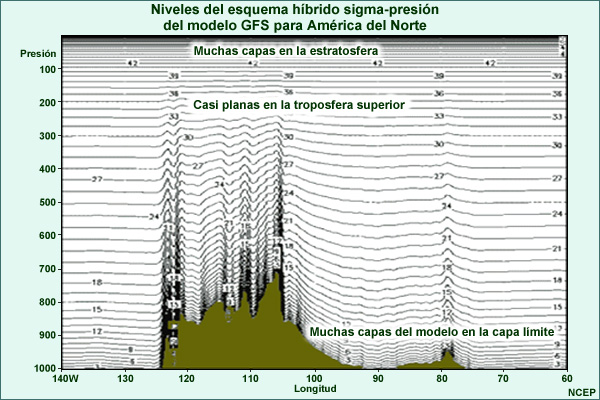
Resumen
General
La resolución vertical de los modelos operativos debe ser tal que permita:
- incorporar los efectos del calentamiento y enfriamiento diurno;
- incorporar los efectos locales de las variaciones espaciales de las características superficiales;
- describir el flujo y la cortante del viento en la capa límite;
- capturar los regímenes ageostróficos asociados con las corrientes en chorro en la alta troposfera;
- detectar las interacciones entre la estratosfera y la troposfera, incluyendo múltiples chorros de alto nivel;
- seguir los regímenes en la estratosfera que afectan los pronósticos a mediano plazo y las concentraciones de gases traza.
Para lograr todo esto, ha sido necesario encontrar un justo medio entre los beneficios de añadir capas para mejorar los pronósticos de los modelos numéricos y los costos de hacerlo.
Coordenadas específicas
Esta tabla ofrece un resumen de las ventajas de los diferentes sistemas de coordenadas verticales en la descripción de algunos procesos atmosféricos.
| Sistema de coordenadas | Adaptabilidad de las capas | Regiones de la atmósfera bien representadas |
|---|---|---|
| Sigma |
|
|
| Híbrido sigma-isobárico |
|
|
| Híbrido isoentrópico-sigma |
|
|
* Observe que, independientemente del sistema de coordenadas verticales que utilicen, los modelos espectrales están más limitados, porque emplean intervalos de tiempo mayores que pueden producir cierta inestabilidad numérica cuando se producen los movimientos verticales fuertes en regiones de resolución fina (capas delgadas del modelo). Aunque la inestabilidad numérica es algo muy raro en los modelos operativos, ha ocurrido tanto en modelos de malla como espectrales, principalmente cerca de corrientes en chorro muy intensas. Este fenómeno se manifiesta por una región de oscilaciones en todos los campos del modelo, la cuales no tienen un origen físico y producen isohipsas recortadas incluso sobre los océanos, donde no es posible que una serie de ondas de montaña constituya la base física de su formación.
Dominio y condiciones de frontera
Introducción
Introducción
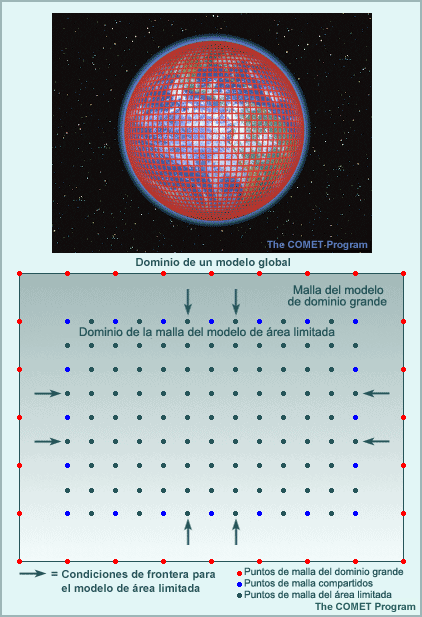
Por dominio del modelo se entiende el área de cobertura del modelo. Los modelos de área limitada tienen fronteras horizontales (laterales) y verticales (superior e inferior), mientras que los modelos globales, que por su naturaleza abarcan todo el planeta, solo tienen fronteras verticales.
Los modelos de dominio mayor aportan los datos para las condiciones de fronteras laterales de los modelos de área limitada. Todos los modelos deben contar con información exacta de todas las variables de pronóstico en el dominio y a lo largo de cada frontera del modelo (lateral, superior e inferior) para poder resolver las ecuaciones de pronóstico. Los valores de frontera pueden provenir de varias fuentes, incluyendo:
- sistemas de asimilación de datos;
- valores de pronóstico de un ciclo de ejecución actual o anterior de un modelo de gran escala (como es el caso para las condiciones de fronteras laterales en los modelos de área limitada);
- algún valor climatológico o fijo (para especificar ciertas características de superficie, como la humedad del suelo, la temperatura superficial del mar y el tipo de vegetación).
*Pregunta
Pregunta
Considere su experiencia con los modelos predicción numérica del tiempo para describir algunos de los aspectos fundamentales relacionados con el dominio del modelo que hay que considerar al utilizar la guía del modelo, particularmente la de los modelos de área limitada. Escriba su respuesta en el espacio siguiente.
Comentario
Al estudiar la guía del modelo es importante tener presente:
- La proximidad del área de pronóstico local a las fronteras del modelo, dada la mayor probabilidad de que los errores se propaguen hacia adentro desde las fronteras durante el ciclo de pronóstico.
- La calidad y la resolución del pronóstico del dominio de mayor escala utilizado para proveer las condiciones de frontera para el modelo de área limitada. Las deficiencias en ese pronóstico afectarán al modelo de menor dominio y amplificarán los errores durante el período de pronóstico. Algunos ejemplos comunes son los errores en la ubicación, intensidad y estructura de las depresiones, los frentes, las corrientes en chorro y varias otras estructuras.
- Las condiciones de la frontera inferior (aquellas que describen muchos de los procesos físicos que ocurren en o cerca de la superficie terrestre), especialmente su descripción y la exactitud de las parametrizaciones utilizadas para determinarlas. La exactitud de la descripción de los procesos físicos es esencial para el pronóstico de muchos elementos sensibles del tiempo, como la temperatura, el viento, la turbulencia y la precipitación.
Dominio y condiciones de frontera

El dominio de un modelo de PNT se puede concebir como una matriz tridimensional de cubos similar a la que se ilustra en la figura. Cada cubo encierra un volumen de la atmósfera que corresponde a un punto de malla del modelo. Los valores del pronóstico para las variables meteorológicas en cada cubo se derivan de los valores reales dentro del cubo más los de los cubos circundantes. Debido a que no hay cubos en todos los lados de los cubos en las fronteras, la información necesaria para incorporar valores de pronóstico para los parámetros meteorológicos no se puede determinar solo con los datos contenidos en el modelo. La información para las fronteras exteriores debe provenir de otra fuente.
En el resto de la sección «Dominio del modelo y condiciones de frontera» se plantean estos y otros temas relacionados con las condiciones de frontera verticales y laterales, incluyendo los métodos utilizados para incorporar las variables meteorológicas externas al dominio del modelo y los errores introducidos en el dominio del modelo por las condiciones de frontera.
Condiciones horizontales y anidamiento
Impactos de las fronteras
Los métodos aquí descritos se aplican solo a los modelos de área limitada y se utilizan para brindar la información necesaria acerca de los cambios en las variables meteorológicas de pronóstico que ocurren fuera del dominio del modelo.
En términos ideales, las condiciones de frontera deberían provenir de datos observados (como es el caso en la investigación de casos de estudio). Sin embargo, lo mejor que se puede hacer en el pronóstico del tiempo es usar condiciones de frontera provenientes de otro modelo de pronóstico.
La calidad del pronóstico de los modelos de área limitada o locales se ve fuertemente afectada por la calidad de los pronósticos producidos por el modelo que brinda las condiciones de fronteras laterales. Los errores en el pronóstico de los modelos de dominio mayor se trasladarán al dominio de pronóstico del modelo de área limitada y pueden, en algunos casos, amplificarse. Por ejemplo, los modelos de alta resolución se limitan a regiones reducidas debido a la fuerte demanda en los recursos de cómputo que implica ejecutar una malla tan fina. Los errores similares a los del modelo que produce las condiciones de frontera pueden propagarse rápidamente por el dominio limitado del pronóstico del modelo de alta resolución.
Las condiciones de fronteras laterales controlan en gran medida la posición y la evolución de las estructuras que cubren todo el dominio de pronóstico. Por ejemplo, para un dominio que cubre el territorio continental de Estados Unidos, los patrones de onda larga vienen determinados casi enteramente por las condiciones de frontera. Se pueden notar impactos más débiles en las zonas de máximos de velocidad de las corrientes en chorro y los frentes, especialmente en regiones corriente abajo alejadas de la frontera. De forma análoga, en un modelo de mesoescala de alta resolución que se ejecuta para una zona pequeña, la ubicación espacial y temporal de las estructuras de escala sinóptica viene determinada casi por completo por el modelo de escala sinóptica que aporta las condiciones de frontera.
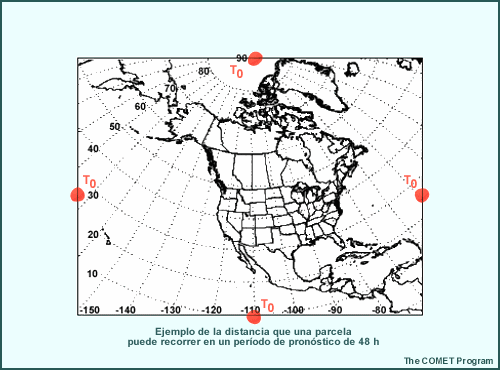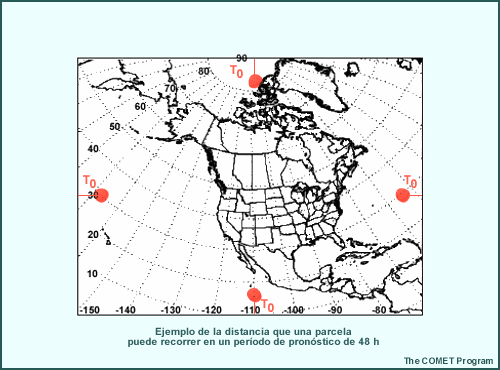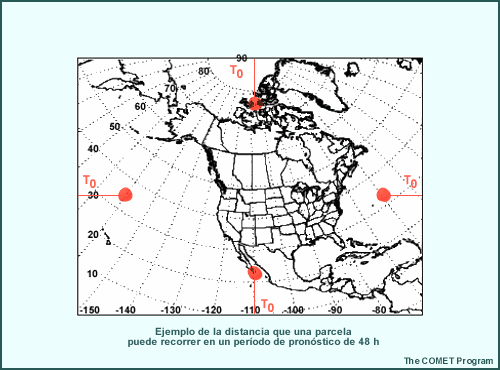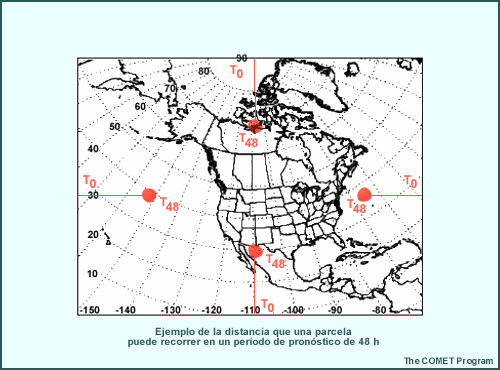
La animación ilustra la distancia que una parcela de aire puede recurrir en el dominio de un modelo de área limitada ficticio desde la frontera del modelo durante un período de pronóstico de 48 horas con un viento de aproximadamente 15 m/s. ¡Un chorro de 60 m/s puede transportar una parcela de aire de un lado a otro de este domino en 48 horas! Dado que la influencia de las condiciones de frontera se propaga desde las fronteras (particularmente corriente abajo) y que en algunos casos los efectos se amplifican corriente abajo, el área de pronóstico de interés principal debería estar ubicada tan lejos de las fronteras como sea posible, especialmente de la frontera corriente arriba. Debido a que el viento transporta parte la influencia de la frontera, la velocidad y la dirección de mayor impacto para el pronóstico variarán de un régimen de flujo a otro. Es importante prestar atención a la duración de una trayectoria entre la frontera del modelo y la zona cercana al área de pronóstico.
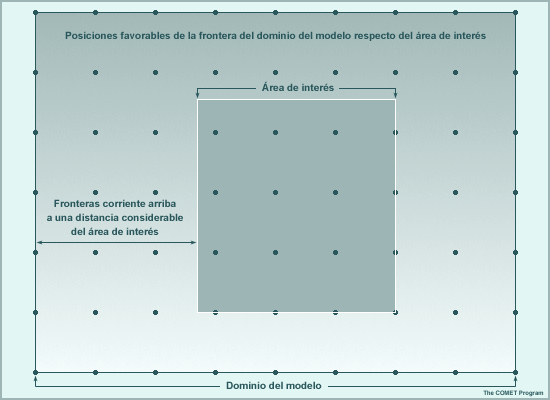
El gráfico muestra una configuración favorable de las fronteras del modelo en relación con el área de pronóstico de interés. Note que las fronteras (especialmente a lo largo de la porción corriente arriba del dominio del modelo) están alejadas del área de interés. Al ubicar la frontera corriente arriba fuera del área de pronóstico, se puede reducir la influencia de los errores de frontera dentro del área de interés. Es importante destacar que en este caso ideal el dominio de pronóstico total del modelo es casi cuatro veces mayor que el área relativamente pequeña de pronóstico que es de interés primordial. A medida que el tamaño de esta zona aumenta, el tamaño relativo de la porción del dominio de pronóstico total que se «desperdicia» para prevenir los errores asociados con las condiciones de frontera disminuye.
Interacción unidireccional
Normalmente, las condiciones de fronteras laterales se obtienen de la ejecución previa de un modelo de dominio mayor. Por ejemplo, un pronóstico de 6 a 54 horas de un modelo global ejecutado a las 06 UTC puede proporcionar las condiciones de fronteras laterales para un pronóstico de 0 a 48 horas de un modelo regional que empieza a las 12 UTC. La información fluye en una dirección, del pronóstico previamente integrado del modelo de dominio mayor al modelo de dominio menor. Por lo tanto, esta interacción se denomina unidireccional.
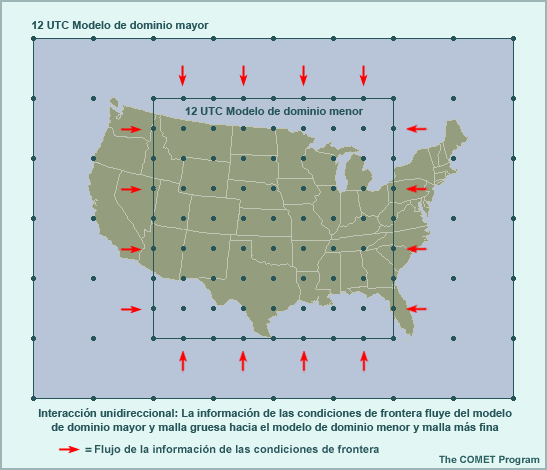
Interacción bidireccional
Algunos modelos de área limitada, incluyendo el UW-NMS, el ARPS y el MM5, se ejecutan con mallas de área reducida y resolución fina anidadas dentro de mallas de resolución más gruesa en el mismo modelo. Es necesario anidar mallas de este modo porque las limitaciones de memoria y velocidad de los equipos informáticos no permiten utilizar las mallas de resolución fina para cubrir el dominio completo del modelo.
La información para las fronteras más externas de estos modelos de mallas anidadas proviene de una fuente externa, utilizando interacción unidireccional. Sin embargo, los puntos de contacto entre las mallas dentro del modelo de mallas anidadas se determinan con los pronósticos obtenidos dentro del modelo mismo.
Donde la malla fina cubre la malla gruesa, las variables de pronóstico para la malla gruesa se actualizan con el pronóstico de la malla fina. El pronóstico de la malla gruesa, a su vez, afecta al pronóstico de malla fina al entregar las condiciones de frontera en la zona de contacto entre las mallas. Dado que la información fluye en ambos sentidos, esta interacción se denomina bidireccional.
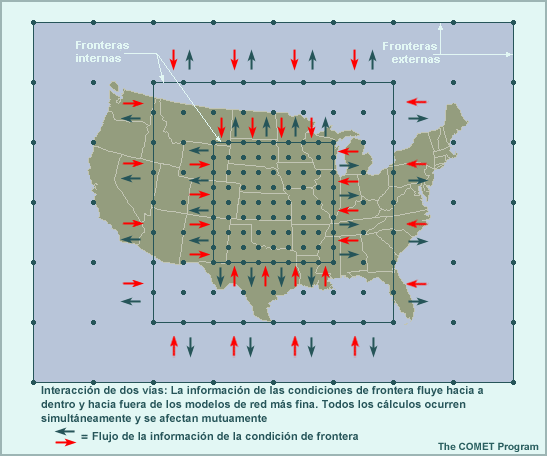
La interacción bidireccional tiene muchas ventajas por distintas razones.
- Permite que los procesos resueltos por la escala fina influyan en el flujo de mayor escala en la malla gruesa. Por ejemplo, un sistema convectivo a gran escala resuelto en la malla fina puede amplificar una dorsal en altura, lo cual vuelve más lento el progreso de las ondas en los vientos del oeste en la malla de resolución gruesa del dominio mayor.
- Debido a que las predicciones en las mallas de resolución gruesa requieren un tiempo de cálculo y recursos de memoria relativamente pequeños, la frontera más externa del modelo puede ubicarse lejos de la región de interés del pronóstico, mientras que el dominio de resolución fina se mantiene suficientemente pequeño como para ejecutar el modelo en tiempo real.
- El uso de estos procedimientos de condición de frontera en «tiempo real» dentro de un modelo con la misma dinámica y física básica del pronóstico reduce considerablemente el efecto de los errores asociados con la utilización de las condiciones de frontera de un modelo con datos menos recientes y coordenadas verticales, topografía y física diferentes.
Fuentes de error
La siguiente es una lista de los factores relacionados con las condiciones de frontera que pueden causar error en el pronóstico de un modelo. Para algunos de los factores tiene que contestar una serie de preguntas.
1. La exactitud del pronóstico generado por el modelo que proporciona las condiciones de frontera.
Antigüedad del pronóstico que proporciona las condiciones de frontera
Recuerde que el modelo se ejecutó antes que el modelo de área limitada, de modo que puede tener datos menos recientes y haber sido iniciado muchas horas antes.
Características y procesos de pequeña escala ausentes en las condiciones de frontera proporcionadas por el modelo de dominio mayor
Pregunta
¿Cuáles son los posibles impactos en el pronóstico subsiguiente del modelo? Escriba su respuesta en el espacio siguiente.
Comentario
Las estructuras atmosféricas que se pueden resolver con el modelo de malla más fina pueden ser menos pronunciadas (o no aparecer en absoluto) que en los campos de pronóstico del modelo de malla más gruesa que proporciona las condiciones de frontera, de manera que estas características no se pueden mover apropiadamente al dominio de pronóstico de la malla más fina. Es posible que el modelo de malla más fina trate de desarrollar estas estructuras con el tiempo, pero no se pronosticarán cerca de la frontera corriente arriba. Incluso su exactitud corriente abajo puede verse afectada, porque su ciclo de vida fue atrasado.
Condiciones de frontera con una descripción insuficiente de los gradientes
Pregunta
¿Cuáles son los posibles impactos en el pronóstico de un fuerte sistema frontal que se mueve de un modelo de resolución gruesa al dominio de un modelo de resolución más fina? Escriba su respuesta en el espacio siguiente.
Comentario
Las condiciones de frontera que representan promedios de las variables meteorológicas en la celda de malla grande de un modelo de resolución gruesa limitarán la intensidad de los gradientes y sus efectos, como la frontogénesis, cerca de las fronteras laterales del modelo de resolución más fina. Esto limitará el modelo de resolución más fina en su capacidad de desarrollar los gradientes adecuados asociados con el sistema frontal. Este efecto se mantendrá cerca de las fronteras a lo largo del ciclo de pronóstico, pero no se propagará hacia adentro durante el período de pronóstico.
2. Diferencias en la formulación del modelo entre los modelos de mayor escala y los de escala más fina
Las parametrizaciones físicas y las formulaciones dinámicas del modelo que provee las condiciones de fronteras laterales pueden ser diferentes de las del modelo de dominio más pequeño, lo cual puede llevar a errores en el pronóstico. Los siguientes son ejemplos de diferencias de formulación y los errores de pronóstico que pueden causar.
Incoherencias dinámicas dentro del modelo debido al uso de coordenadas verticales diferentes en los dos modelos
Dado que las configuraciones de coordenadas verticales no resuelven las ecuaciones de pronóstico de forma idéntica, los balances dinámicos entre los campos de masa y de viento pueden verse alterados a lo largo de las celdas de malla fronterizas si se utilizan coordenadas verticales sustancialmente diferentes. Esto genera ondas falsas en la frontera. Por lo tanto, es importante que las coordenadas verticales coincidan en la frontera.
Diferencias en la resolución vertical
Las diferencias en el número de capas verticales y el espesor y la distribución de las capas a lo largo de las fronteras laterales pueden crear problemas al definir la estructura vertical de las estructuras atmosféricas que están cerca o a punto de penetrar el dominio del pronóstico. Por ejemplo, una capa delgada de humedad cercana a saturación en un modelo que provee las condiciones de frontera puede dispersarse en dos o más capas en un modelo de área limitada. En el proceso, la mezcla con aire más seco por arriba y por debajo de dicha capa puede inadvertidamente eliminar la condición de casi saturación proveniente de la frontera.
Diferencias de topografía en la frontera
Si la altura de la superficie terrestre no está totalmente alineada en la frontera de los dos modelos, puede resultar necesario recurrir a extrapolaciones verticales para «rellenar los huecos» en el modelo de red más fina. Debido a que estas extrapolaciones suelen realizarse sobre la base de una variedad de supuestos y aproximaciones, se pueden introducir errores sustanciales en los campos de pronóstico de bajo nivel. Por lo tanto, es preferible localizar las fronteras sobre terreno de bajo nivel y topografía suave, en la medida de lo posible.
Parametrizaciones convectivas diferentes que pueden causar que el aire que entra a través de la frontera active inmediatamente la parametrización convectiva en el modelo de red fina
Pregunta
¿Qué posibles impactos puede tener la existencia de parametrizaciones convectivas diferentes sobre los pronósticos de precipitación dentro del dominio del modelo de resolución más fina? Escriba su respuesta en el espacio siguiente.
Comentario
Esto puede resultar en pronósticos de lluvias fuertes en la frontera y posiblemente muy poca lluvia e inestabilidad corriente abajo. Lo opuesto puede ocurrir también, cuando la red fina es incapaz de generar convección debido a una descripción inadecuada del contenido de humedad y de la estabilidad del aire que fluye a través de la frontera a partir del modelo de dominio mayor.
Hidrometeoros pronosticados por un modelo pero no por el otro
Esto ocasiona incoherencias entre la cantidad de humedad en los datos de frontera y el modelo de área limitada, lo cual crea problemas para el pronóstico de nubosidad y precipitación
Diferencias en la representación de los procesos físicos
Diferencias en la especificación o el tratamiento de los procesos que ocurren en la atmósfera cerca de la superficie terrestre (como la parametrización de la convección, la temperatura de la superficie del mar, la evaporación de la humedad del suelo a la capa límite, o el manto de nieve) pueden causar estragos cerca de las fronteras y perturbar el desarrollo de las estructuras que deberían fluir hacia adentro del dominio de área limitada.
*Refracción de ondas
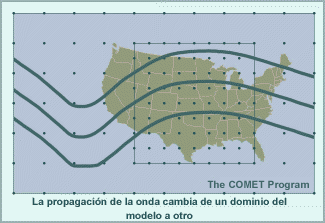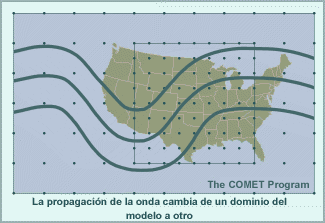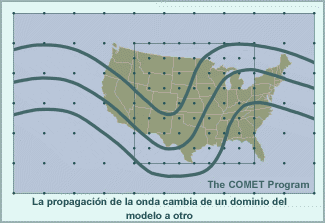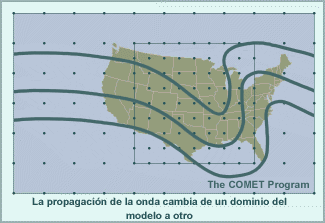
En el punto de contacto entre mallas de diferente resolución, las ondas atmosféricas en un modelo numérico actúan de forma muy parecida a las ondas de luz en la interfase entre el aire y el agua.
La velocidad de propagación de una onda en un modelo varía con el número de puntos utilizados para representar la onda. El movimiento de una onda bien resuelta se pronosticará con la velocidad correcta, mientras que el de una onda de resolución pobre se pronosticará con una velocidad menor a la verdadera. Esto significa que una onda que pasa por una zona de contacto entre mallas puede doblarse, cambiando su orientación como se ilustra en la animación. Además, las condiciones de frontera pueden forzar un movimiento más lento de la onda sobre la malla de resolución menor, interrumpiendo la mejor solución cerca de la frontera. En el peor de los casos, se puede dar la reflexión de una onda en una frontera del modelo o de la malla. Sin embargo, las mejoras realizadas recientemente en los métodos numéricos reducen o eliminan este comportamiento.
Debido a que este error solo afecta las ondas de resolución pobre en la malla más gruesa que aporta las condiciones de frontera, en los modelos actuales suele afectar únicamente la estructura de mesoescala, y no se dan los efectos sobre las ondas de gran escala, como en el pasado. Las siguientes estructuras meteorológicas pueden verse afectadas por la refracción o el cambio de dirección de las ondas atmosféricas en las fronteras laterales de un modelo:
- campos de precipitación
- campos de temperatura
- estructura de máximo de velocidad de corriente en chorro
- campos de movimiento vertical
- intensidad y ubicación de depresiones y frentes en la superficie asociados a pequeñas ondas cortas e intensas
Este tipo de error se volverá menos evidente a medida que mejore la resolución de los modelos globales.
Fronteras superior e inferior
*Superior
Todos los modelos de pronóstico, incluidos los modelos globales, requieren que se especifiquen condiciones de frontera en la parte superior e inferior del dominio del modelo.
La parte superior de los modelos se ubica muy por encima de la tropopausa. Es necesario realizar suposiciones sobre cómo las variables de pronóstico arriba del límite superior elegido cambiarán a lo largo del período de pronóstico.

En la mayoría de los modelos se establece una condición de frontera superior rígida, lo cual significa que no se permiten movimientos verticales a través del límite superior del modelo. Pueden surgir problemas cuando las ondas de gravedad (como aquellas generadas por la convección en el modelo o por el flujo sobre la topografía del modelo) se reflejan en la frontera superior del modelo. Si esto no se toma en consideración, estas ondas de gravedad pueden «rebotar» a través de todo el espesor del modelo y afectar en gran medida los pronósticos de movimiento vertical y de precipitación. Afortunadamente, se han desarrollado tratamientos numéricos especiales, como la adición de una capa de «absorción» o de «atenuación» cerca del límite superior del modelo, para evitar este problema. Estos tratamientos solo se pueden aplicar cuando el límite superior del modelo se encuentra mucho más arriba de cualquier característica meteorológica a pronosticar, dado que el pronóstico para las capas más altas del modelo no es realista.
Inferior
La frontera inferior es definida por la zona de contacto entre el nivel atmosférico más bajo del modelo y la topografía o la superficie oceánica del modelo. La exactitud con la que esta condición de frontera representa las condiciones de la superficie terrestre depende del tratamiento físico de la superficie y las parametrizaciones utilizadas en el modelo, así como también de la fuente de la información de cobertura de nieve, temperatura y humedad del suelo, tipo de suelo y vegetación.

El movimiento vertical en el suelo es cero, con excepción de la componente pendiente arriba o abajo debida al flujo a lo largo de la topografía del modelo. Los vientos horizontales se pronostican como un promedio para la capa inferior, no para el suelo o el nivel de anemómetro. Los vientos cerca de la superficie se determinan empíricamente.
Dado que la mayoría de los modelos utilizan principios de balance de energía para pronosticar las condiciones cerca de la superficie, se introducirán errores por manejo inadecuado del terreno, el albedo, la cantidad de agua de lluvia disponible para la evaporación en la superficie, la temperatura de lagos y océanos, la cobertura de vegetación, el método para simular la interacción suelo-vegetación-atmósfera, y muchos otros detalles relacionados con la representación de los procesos físicos en el modelo. Esto se trata más a fondo en la sección sobre física de este curso.
Impactos en el pronóstico
Para lograr pronósticos exactos, los modelos de pronóstico operativos incorporan tantos modelos de procesos de superficie capaces de producir resultados físicos significativos como es posible (tomando en cuenta lo límites computacionales). Los modelos de PNT actuales incluyen interacciones acopladas atmósfera-tierra (incluyendo pronósticos de humedad del suelo, vegetación y nieve). En el futuro, los modelos acoplados atmósfera-tierra serán aún más sofisticados con el fin de mejorar la descripción y el pronóstico de las condiciones superficiales, y probablemente se incorporarán modelos atmósfera-océano para permitir una verdadera unión entre la atmósfera y las superficies de agua.
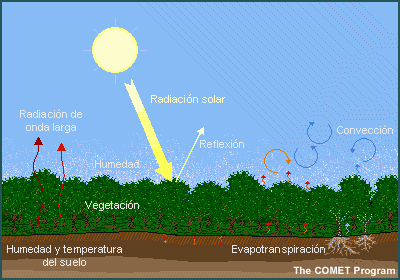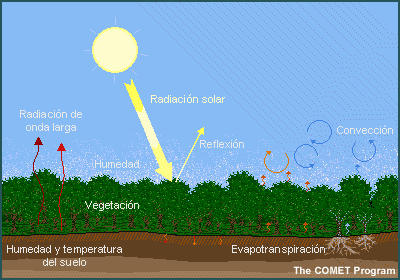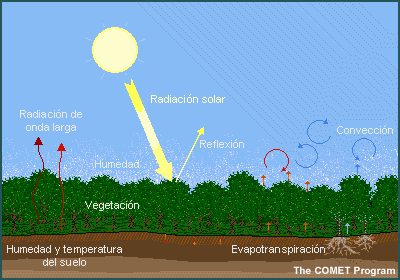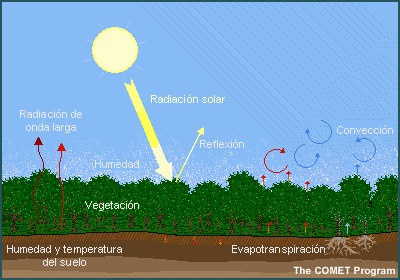
Dado que los modelos utilizan las características de superficie como parte de las condiciones de frontera inferior, se pueden introducir errores debido a los siguientes factores.
- La superficie no está
descrita
con
suficiente resolución como para
capturar las condiciones
necesarias para producir un
pronóstico
exacto.
Por ejemplo, una descripción inadecuada de las características del terreno local puede resultar en la ubicación incorrecta o la inexistencia de masas de aire de tormentas eléctricas en una cierta parte del área de pronóstico, como cerca de las pendientes de las montañas o los bordes de los embalses. Las características del terreno a escala local pueden estar contenidas completamente dentro de una o dos celdas de la malla, y por ende los pronósticos de los fenómenos que estas características pueden inducir no son buenos.
- En lugar de observaciones
atmosféricas,
se usan datos del modelo para
determinar las condiciones de
superficie, de manera que los sesgos y
errores del
modelo generan sesgos y errores
adicionales en las condiciones
de superficie.
Por ejemplo, es común utilizar la precipitación del pronóstico para determinar la humedad del suelo. Un sesgo hacia la precipitación en el modelo causaría un sesgo en la humedad del suelo, lo cual ocasiona un sesgo hacia temperaturas más frías, evaporación excesiva y humedad de bajo nivel. Por retroalimentación también se puede amplificar el sesgo existente hacia alta precipitación en el modelo.
- Las especificaciones del modelo no
reflejan con
exactitud las condiciones
superficiales reales que
afectarán
al pronóstico
local.
Por ejemplo, en algunos modelos, las temperaturas superficiales de los lagos se ajustan al promedio zonal de la temperatura de la superficie del mar (TSM) global en lugar de la verdadera temperatura de los lagos. El impacto de este modo de proceder es mínimo en los modelos de resolución gruesa (dado que no pueden resolver adecuadamente los lagos y su impacto en el tiempo), pero puede tener un impacto considerable en los modelos de resolución más fina. Además, en ciertas zonas hasta los lagos de extensión considerable pueden congelarse, pero debido a una insuficiencia de datos el modelo sigue considerándolos cuerpos de agua. Esto puede producir errores grandes en el pronóstico local e incluso errores de análisis en los modelos de alta resolución.
- Los procesos que afectan los
pronósticos
de los modelos no se representan
apropiadamente en el
modelo.
Un buen ejemplo es la interacción atmósfera-océano. Se ha mostrado que la temperatura de la superficie del mar (TSM) puede tener un ciclo diurno de hasta 3 °C en condiciones casi calmas. La mayoría de los modelos de PNT conservan el valor de TSM inicial a lo largo del período de pronóstico. Esto puede causar que los modelos subestimen la evaporación diurna de la superficie del océano, lo cual afecta la provisión de humedad de bajo nivel hacia las áreas terrestres cercanas. NCEP está trabajando en acoplar el modelo GFS a un modelo oceánico, y los modelos de huracanes ya son acoplados, de modo que la tormenta puede determinar la marejada y reducir la TSM, todo lo cual a su vez reduce la intensidad de la tormenta. Sin embargo, el modelo NAM de NCEP y los modelos de mesoescala que se ejecutan a nivel local sin un modelo oceánico no pueden representar este tipo de retroalimentación.
Es extremadamente importante tomar en consideración las deficiencias de la guía del modelo durante los procesos de preparación del pronóstico. Los procesos superficiales ejercen una influencia tremenda en el tiempo sensible cerca del suelo y en las variaciones locales en el área de pronóstico. Desafortunadamente, la representación de estos procesos es extremadamente difícil y contribuye fuertemente a los errores en el pronóstico. Sin embargo, nuestra habilidad con el pronóstico puede compensar estos errores.
Vea la sección de física de este curso y la Operational Models Encyclopedia para obtener más información sobre el impacto de las condiciones físicas de frontera en el pronóstico del modelo y los pasos que se pueden tomar para modificar el pronóstico de manera que se tomen en cuenta las condiciones físicas de frontera reales.
Pregunta 1
Pregunta
De los componentes del modelo enumerados a continuación, ¿cuáles son los cinco que tienen mayor impacto en la exactitud de la información de las condiciones de frontera para la capa superficial del dominio vertical de un modelo? Escoja todas las opciones pertinentes.
Comentario
La información de las condiciones de frontera depende en gran medida de la resolución horizontal (a), la resolución vertical (b), la coordenada vertical (c), la exactitud del pronóstico de precipitación (d) y la física de la radiación y de la superficie (e), es decir, la exactitud de la física utilizada para definir las propiedades y los procesos superficiales.
- La resolución horizontal afecta la posición del terreno y los litorales en el modelo. El terreno afecta la altitud a la cual los flujos de superficie se perciben en la columna atmosférica, y el cambio en la definición de una celda de tierra firme a agua (y viceversa) en la malla afecta la rapidez con que la superficie se enfría o se calienta y los flujos hacia la columna atmosférica.
- La resolución vertical influye en la medida en que se definen las capas inferiores de la atmósfera, ya que dicta el número de capas que definen la atmósfera inferior.
- La elección de las coordenadas verticales determina si la capa inferior del modelo interseca la superficie terrestre (por ejemplo, coordenadas de presión, altura o isoentrópicas) o sigue el terreno (coordenada sigma). Esto afecta el grosor de la capa inferior del modelo (p. ej.: más delgada sobre terreno más alto en el caso de la coordenada sigma, o bajo condiciones estables, para la coordenada isoentrópica) y, por tanto, cómo se transfieren los flujos a la capa límite del modelo.
- La exactitud del pronóstico de precipitación (ubicación y cantidad) afecta a la humedad del suelo en los modelos. Los errores en la precipitación y, por ende, en la humedad del suelo, alteran la cantidad de energía solar incidente que se gasta en evaporación. Esto afecta la temperatura del suelo, lo cual afecta la temperatura del aire de bajo nivel y la humedad cerca de la superficie.
- La física del modelo caracteriza y describe muchos procesos en la capa superficial que luego se utilizan para definir las condiciones de la frontera inferior. Es importante saber cuáles procesos o características se parametrizan o se pronostican en un modelo en particular (por ejemplo, humedad del suelo, nieve y albedo) para poder identificar las fortalezas y debilidades del modelo al definir las condiciones de frontera inferiores.
Cada uno de estos componentes del modelo afecta las condiciones de frontera de una manera específica, pero en última instancia todos están relacionados.
Pregunta 2
Pregunta
¿Cuáles de los siguientes parámetros de bajo nivel de la salida del modelo se ven afectados directamente por la exactitud de la información de las condiciones de frontera en la capa superficial del modelo? Escoja todas las opciones pertinentes.
Comentario
Todas las opciones son correctas. Las condiciones de frontera superficiales inexactas pueden tener un impacto adverso en casi todos los procesos que interactúan con la capa superficial.
Mitigación de errores
Aunque es importante que todos los usuarios de la guía de un modelo entiendan cómo las condiciones de frontera inexactas o inapropiadas pueden introducir errores en el análisis y en los pronósticos de un modelo, también deben saber ajustar el pronóstico en base a su conocimiento de estos errores.
Pregunta
¿Qué métodos podemos utilizar para mitigar algunos de los errores introducidos por las condiciones de frontera? Escriba su respuesta en el espacio siguiente.
Comentario
Un método que está fuera de las posibilidades de la mayoría de los usuarios de PNT implica crear características tales como física y parametrizaciones más exactas, y mejorar la habilidad del modelo para representar los procesos y las características que se producen en las fronteras del modelo. Por ejemplo, se hace un esfuerzo considerable para mejorar los procesos físicos de los modelos, y las mejoras en la descripción de las características y los procesos superficiales deberían reducir el error introducido por las condiciones de la frontera inferior.
Sin embargo, los usuarios de PNT pueden aplicar otro método, es decir, utilizar herramientas de diagnóstico para evaluar la exactitud de los campos iniciales del modelo y los pronósticos a corto plazo cerca de las fronteras del dominio. Se pueden utilizar las imágenes de satélite, los datos de superficie y de altura, los perfiladores, los radares y otras herramientas para comparar las condiciones reales con las del modelo. Este proceso es especialmente valioso cerca y fuera de las fronteras laterales del modelo para poder mejorar su descripción de las características cerca de las fronteras y el pronóstico de las características que entrarán en el dominio durante el ciclo de pronóstico.
Esta aproximación es más subjetiva y se requiere cierta habilidad para interpretar y comparar las distintas fuentes de datos con los campos iniciales del modelo. Sin embargo, es posible hacer ajustes subjetivos que nos ayuden a entender dónde el modelo se desvía de la realidad. También podemos hacer ajustes subjetivos posteriores en los campos de pronóstico para tomar en cuenta los errores del modelo previamente identificados. Este método, que no es a prueba de errores, ayuda a eliminar y ajustar los errores de fronteras laterales introducidos en el análisis y el pronóstico del modelo.
Preguntas
*Impactos del dominio
Pregunta
Asigne a cada elemento del dominio la característica o el impacto que le corresponde. Haga clic en una característica o un impacto en la derecha y arrástrelo al elemento del domino correcto en la izquierda.
Explicación
Frontera superior del modelo = Reflexión de las ondas. En algunos modelos la frontera superior es como un barrera física que la energía de onda que se propaga en sentido vertical no puede penetrar. La energía de onda se refleja hacia abajo y a veces interactúa con otras ondas. Esto puede introducir errores en el movimiento vertical y los campos relacionados, como la precipitación.
Modelos de área limitada = Requieren interpolación de datos en las fronteras del modelo. Por su naturaleza los modelos de área limitada requieren que se interpolen los datos provenientes del dominio de modelo más grande para brindar las condiciones de fronteras laterales de entrada para la malla anidada.
Fuente de las condiciones de fronteras laterales = Calidad de los datos de frontera introducidos. Cuando un modelo de dominio más grande proporciona las condiciones de fronteras laterales, la calidad del pronóstico del modelo de dominio más grande se debe siempre tener presente, porque puede afectar la calidad de las condiciones de frontera del modelo de malla más fina.
Global (malla continua) = Sin fronteras laterales. Debido a que la malla de los modelos globales abarca todo el planeta, estos no requieren condiciones de fronteras laterales. Esto constituye una ventaja, ya que implica una fuente de error menos que se puede introducir en el dominio del modelo.
Interacción entre mallas = Intercambio de información unidireccional o bidireccional en las fronteras. Hay dos tipos de interacción entre mallas: unidireccional y bidireccional. En las interacciones bidireccionales, las dos mallas del modelo pueden afectarse mutuamente, y esta es una verdadera ventaja que puede redundar en pronósticos más exactos. En el caso de las interacciones unidireccionales, solo el modelo de dominio más grande puede afectar al modelo de malla más fina.
Condiciones de frontera con la capa de superficie = Exactitud de representación de las características y los procesos físicos. Las condiciones de frontera en la superficie pueden afectar la exactitud de representación de los procesos y las características físicas de la superficie. Las carencias en la física del modelo pueden introducir errores en la caracterización de la superficie terrestre, 10 cual, a su vez, propagará los errores en muchos procesos de la atmósfera inferior.
*Modelos globales y de área limitada
Pregunta
Haga clic en todos los elementos pertinentes al dominio de cada modelo. Escoja todas las opciones pertinentes.
Las respuestas correctas son (a), (d), (f), (g), (h), (i) y (j).
Los modelos globales tienen una frontera superior y en la capa de superficie. Dado que cubren la superficie completa del planeta, no tienen fronteras laterales y no interactúan con las mallas de un modelo de dominio mayor.
Los modelos de área limitada tienen fronteras laterales, superior e inferior. La frontera superior puede ser especialmente importante en los modelos de mesoescala y de escala de tormenta diseñados para pronosticar la convección. Los movimientos verticales profundos asociados con la convección pueden verse afectados adversamente si no se trata la frontera superior del modelo de forma adecuada. Además, puede haber interacciones entre múltiples mallas, como ocurre cuando se ejecuta un modelo local con condiciones de frontera derivadas de un modelo de área limitada influenciado por las condiciones de frontera de los modelos de dominio mayor.
Impactos operativos 1
Los ejercicios de esta y las páginas siguientes se centran en los impactos operativos del dominio y las condiciones de frontera del modelo.
Pregunta
Entre las siguientes variables iniciales de frontera inferior seleccione las cuatro que son más sensibles a la falta de datos de observación. Escoja todas las opciones pertinentes.
Comentario
Las
respuestas
correctas son
(b) masa
de
nieve,
(c) humedad
del suelo,
(d)
temperatura superficial del
suelo y
(e) manto
de
nieve.
Por lo general, el desarrollo y el subsiguiente impacto de los errores en las condiciones de frontera inferior iniciales o pronosticadas vienen determinados por tres factores:
- la variabilidad espacial y temporal de la variable de frontera;
- la capacidad del sistema de asimilar los datos para resolver discontinuidades o gradientes en la variable de frontera;
- la existencia de datos para corregir errores en el pronóstico de condiciones de frontera del modelo cuando se reciclan los datos del modelo.
Las variables de superficie que cambian rápidamente con el tiempo y en el espacio son las más susceptibles a errores que pueden afectar profundamente los análisis si no se dispone de datos actualizados. Por ejemplo, si los análisis de manto de nieve y de masa de nieve no están disponibles y se produce un cambio de importancia que no fue pronosticado por el modelo, pueden ocurrir errores grandes en las temperaturas, la humedad y los flujos de calor de la frontera inferior. Si el modelo subestima o exagera el pronóstico de valor de la precipitación, los valores de humedad del suelo serán incorrectos, lo cual influirá en las temperaturas y los flujos de humedad en la frontera inferior. A su vez, esto puede causar errores en los productos de pronóstico del modelo.
La temperatura superficial manifiesta un fuerte ciclo diurno que no siempre se pronostica bien con los modelos numéricos. Si debemos acudir al balance de energía superficial pronosticado para obtener una temperatura superficial inicial, esto puede producir errores significativos.
Otras variables de superficie, como el hielo marino y la temperatura de la superficie del mar, cambian lentamente con el tiempo. Por eso, muchos modelos de PNT no se degradan excesivamente cuando se obliga a los campos de hielo marino a permanecer constantes a lo largo del ciclo de ejecución del modelo. Sin embargo, se debe tener presente que la resolución horizontal de un modelo puede influir en la forma en que la temperatura superficial del mar en la frontera inferior del modelo afecta a la evolución de los sistemas de mesoescala y de escala sinóptica. Esto es particularmente cierto cerca del punto de contacto entre las corrientes marinas frías y calientes (por ejemplo, las corrientes del Labrador y del Golfo) y cerca de las líneas costeras del modelo cuando el contraste de temperatura entre la tierra y el mar es un factor importante.
Impactos operativos 2
Suponga que está al tanto de la siguiente situación de inicialización del modelo numérico que va a utilizar para generar un pronóstico.
Los análisis de manto de nieve y de masa de nieve no están disponibles para el análisis matutino luego de una importante tormenta de nieve que fue subestimada en el pronóstico del modelo. El pronóstico de masa de nieve del modelo indicaba un equivalente en agua de 3 mm, pero el verdadero valor estimado es de 12 mm de equivalente en agua sobre las celdas de la malla que representan la región. En la segunda mitad de marzo, la radiación solar ya es un factor importante en el ciclo diurno de temperatura. Según en el pronóstico del modelo, la masa de nieve local desaparecerá de la superficie del modelo en las próximas 12 horas.
Pregunta
¿Cómo se debería ajustar la temperatura del aire pronosticada para el día siguiente y por qué? Escoja la mejor respuesta.
Comentario
El pronóstico se vería afectado si la masa de nieve real persistiera durante el período de pronóstico y no se hubiera incluido correctamente en el análisis inicial. Las temperaturas cerca de la superficie en el modelo y los productos de pronóstico del modelo serían mayores que en la realidad debido al impacto en el balance de energía superficial del manto de nieve [a través de la reflexión de la radiación solar por el alto albedo de la nieve y la energía requerida (calor latente de fusión) para derretir la nieve]. Por lo tanto, la respuesta (b) es correcta, mientras que (a) y (c) son incorrectas.
Si bien (d) puede resultar en un mejor pronóstico en el período siguiente, el proceso de pronóstico requiere que se utilice toda la información disponible para hacer el mejor pronóstico posible ahora. En caso contrario, dadas las condiciones del pronóstico debería ser posible determinar si un error en el manto de nieve y en la masa de nieve persistirá en el tiempo o si el error inicial se corregirá automáticamente con un rápido derretimiento de la nieve.
Note que durante los intervalos de tiempo en los que la nieve se derrite rápidamente, pueden ocurrir errores potencialmente grandes en el pronóstico de temperatura del modelo. Esto es especialmente cierto para los modelos que mantienen fija la masa y el manto de nieve a través del período de pronóstico del modelo.
Impactos operativos 3
Un modelo global pronostica 50 mm de lluvia en un período de 12 horas sobre su región durante un evento convectivo de gran escala. La precipitación real fue de 6 a 12 mm. El nuevo pronóstico del modelo se inicializó con un valor de humedad del suelo basado en el pronóstico de lluvia del modelo global. Sin embargo, el área de pronóstico estuvo sufriendo una sequía prolongada.
Pregunta
¿Cómo ajustaría el pronóstico de temperaturas máximas del modelo para el día siguiente y por qué? Escoja todas las opciones pertinentes.
Comentario
La humedad del suelo del modelo puede diferir considerablemente de la humedad real del suelo, lo cual puede afectar la capa límite y el ambiente pronosticado cerca de la superficie. Esto se debe a errores grandes en la precipitación que se producen cuando la tendencia del modelo hacia la climatología es insuficiente para llevar la humedad del suelo hasta un valor cercano a la realidad. Por ejemplo, si se producen lluvias fuertes donde no se pronosticó ninguna o muy poca lluvia, el modelo pronosticará una humedad específica baja cerca de la superficie y una temperatura superficial alta con respecto a la realidad. Además, se pueden producir errores importantes en el pronóstico de las variables cercanas a la superficie y en la baja troposfera si debido a condiciones de inundación o de sequía prolongada la humedad real del suelo en una región es considerablemente distinta al valor con un sesgo hacia la climatología. Por lo tanto, las respuestas (c) y (d) son correctas. Si bien (b) expresa correctamente el error de temperatura del modelo asociado con suelos más secos de lo observado, la situación antes descrita es para suelos que están más húmedos de lo observado.
Nidos de alta resolución
Pregunta
Se ha anidado un modelo de alta resolución de forma unidireccional en un modelo de dominio mayor. El modelo de alta resolución pronostica la evolución de un complejo convectivo de mesoescala (CCM) durante las horas de la noche, algo que no ocurre en el modelo de dominio mayor. Escoja todas las opciones pertinentes.
Comentario
Con el anidamiento unidireccional, la información fluye en una sola dirección. El dominio de resolución más alta no pasa información al dominio más grande de resolución más baja. Esto significa que las opciones (a) y (b) son incorrectas; el nido de alta resolución se puede ejecutar en cualquier momento después de que la información del dominio más grande pase a estar disponible, de modo que la respuesta (c) es correcta. El nido de alta resolución es capaz de resolver estructuras que el modelo de dominio más grande, cuya resolución en más gruesa, no puede resolver, siendo este el motivo por el cual se utiliza un modelo anidado. Por lo tanto, la respuesta (d) es correcta, pero esa información se debe evaluar e interpretar para no llegar a conclusiones equivocadas. Los nidos bidireccionales permiten usar la información del nido de alta resolución en el dominio más grande. Por lo tanto, las opciones (a) y (b) describen lo que ocurriría en un esquema de anidamiento bidireccional.
Resumen
Puntos generales
- Por dominio del modelo se entiende el área de cobertura del modelo.
- Los modelos globales solo requieren condiciones de frontera verticales (superior e inferior), dado que su dominio horizontal cubre todo el planeta.
- Los modelos de área limitada utilizan tanto condiciones de frontera verticales como laterales (horizontales).
- Los modelos de área limitada requieren datos iniciales para las condiciones de fronteras laterales que provienen de modelos de dominio más grande.
- Los efectos de las condiciones de fronteras laterales no solo pueden propagarse por el dominio del pronóstico aproximadamente con la velocidad del viento entrante que atraviesa las fronteras, sino que pueden también afectar los pronósticos cerca de las fronteras. En algunos casos, los efectos corriente abajo pueden amplificarse y moverse hacia adentro con mayor rapidez que la velocidad del viento a lo largo de las fronteras.
- Las condiciones de frontera superior se tratan lo suficientemente bien en la mayoría de los modelos como para causar pocos problemas, pero al preparar el modelo local es preciso asegurarse de que estas condiciones estén configuradas correctamente para evitar problemas en las predicciones del modelo.
- La frontera inferior entra en contacto con la representación del modelo de los procesos superficiales. El hecho de no representar de una forma realista todos los procesos físicos relevantes o de no describir con exactitud el estado físico del suelo genera errores en el pronóstico del modelo.
- Las condiciones de fronteras laterales y las especificaciones de la frontera inferior son fuentes de error principales en el pronóstico del modelo.
Métodos para tratar las interacciones de la frontera lateral
- Interacción unidireccional: La información fluye en una sola dirección, de la malla más gruesa del dominio mayor a la más fina del dominio menor. Los cálculos de la malla más fina no afectan al modelo de dominio mayor.
- Interacción bidireccional: La información fluye en ambas direcciones en los puntos de contacto con la malla interior de un modelo anidado. El pronóstico de la malla más gruesa aporta las condiciones de frontera al pronóstico de la malla más fina, mientras que el pronóstico de la malla más fina se utiliza en la malla más gruesa para determinar las variables de pronóstico.
Métodos para mitigar los errores
- Crear características dentro del modelo, tales como una física y parametrizaciones más exactas, y mejorar su capacidad de representar procesos y características que ocurren en la superficie.
- Corregir las deficiencias conocidas del modelo para representar las condiciones superficiales y los procesos físicos que afectan a las condiciones de superficie.
- Utilizar herramientas de diagnóstico para mejorar la exactitud de los campos de pronóstico inicial y temprano cerca de las fronteras del dominio.
Puntos a recordar cuando se estudia la guía del modelo
- La ubicación del área de pronóstico en relación con las fronteras del modelo.
- La calidad del pronóstico del modelo de dominio mayor que suple las condiciones de frontera para el modelo de área limitada.
- Las condiciones de frontera inferior. En particular, cómo se representan y la exactitud de las parametrizaciones utilizadas para describirlas, cuando se utilizan condiciones pronosticadas de frontera inferior.
Referencias bibliográficas
Tipo de modelo
Carr, F.H., 1988: Introduction to Numerical Weather Prediction Models at the National Meteorological Center. University of Oklahoma, 63 págs.
Conklin, R.J., 1992: Computer Models Used by AFGWC and NMC for Weather Analysis and Forecasting. AFGWC/TN 92/001, Air Weather Service, 69 págs.
Perkey, D.J., 1986: Formulation of mesoscale numerical models. Mesoscale Meteorology and Forecasting, P.S. Ray, Ed., Amer. Meteor. Soc., 573-596.
Petersen, R.A. y J.D. Stackpole, 1989: Overview of the NMC production suite. Wea. Forecasting, 4, 314-322.
Ross, B.B., 1986: An overview of numerical weather prediction. Mesoscale Meteorology and Forecasting, P.S. Ray, Ed., Amer. Meteor. Soc., 720-751.
The COMET Program, 1993: Numerical Weather Prediction, módulo de formación en disco láser presentado por los expertos Dr. Fred Carr y Dr. Ralph Petersen.
Coordenadas verticales
Benjamin, S.G., K.J. Brundage y L.L. Morone, 1994: The Rapid Update Cycle. Part I: Analysis/Model Description. NOAA/NWS Tech. Procedures Bulletin No.416, 16 págs. [Available from the National Weather Service, Office of Meteorology, 1325 East-West Highway, Silver Spring, MD 20910] This is the TPB for the original 60-km RUC-1.
Benjamin, S.G., J.M. Brown, K.J. Brundage, B.E. Schwartz, T.G. Smirnova y T.L. Smith, 1998: RUC-2 - The Rapid Update Cycle Version 2. NOAA/ERL Tech. Procedures Bulletin (Draft).
Black, T.L., 1994: The new NMC mesoscale Eta model: Description and forecast examples. Wea. Forecasting, 9, 265-278.
Black, T.L., D.G. Deaven y G. DiMego, 1993: The step-mountain eta coordinate model: 80-km 'early' version and objective verifications. NOAA/NWS Tech. Procedures Bulletin No. 412, 31 págs. [Available from the National Weather Service, Office of Meteorology, 1325 East-West Highway, Silver Spring, MD 20910.]
Bleck, R. y D.B. Boudra, 1981: Initial testing of a numerical ocean circulation model using a hybrid (quasi-isopycnic) vertical coordinate. J. Phys. Oceanogr., 11, 755-790.
Bleck, R. y S.G. Benjamin, 1993: Regional weather prediction with a model combining terrain-following and isentropic coordinates. Part I: Model description. Mon. Wea. Rev., 121, 1770-1785.
Gallus Jr., W.A y J.B. Klemp, 2000: On the behavior of flow over step orography. Mon. Wea. Rev., 128, 1153-1164.
Hsu, Y.G. y A. Arakawa, 1990: Numerical modeling of the atmosphere with an isentropic vertical coordinate. Mon. Wea. Rev., 118, 1933-1959.
Johnson, D.R., T.H. Zapatocny, F.M. Reames, B.J. Wolf y R.B. Pierce, 1993: A comparison of simulated precipitation by hybrid isentropic-sigma and sigma models. Mon. Wea. Rev., 121, 2088-2114.
Kasahara, A., 1974: Various vertical coordinate systems used for numerical weather prediction. Mon. Wea. Rev., 102, 509-522.
Mesinger, F., 1982: On the convergence and error problems of the calculation of the pressure gradient force in sigma coordinate models. Geophys. Astrophys. Fluid Dyn., 19, 105-117.
Mesinger, F. y Z. Janji , 1985: Problems and numerical methods of incorporation of mountains in atmospheric models. Lectures in Applied Mathematics, 22, 81-120.
Mesinger, F. y T.L. Black, 1992: On the impact on forecast accuracy of the step-mountain (eta) coordinate. Meteor. and Atmos. Phys., 50, 47-60.
Mesinger, F., Z. Janji , S. Ni kovi y D. Gavrilov, 1988: The step-mountain coordinate model: Model description and performance for cases of alpine lee cyclogenesis and for a case of an Appalachian redevelopment. Mon. Wea. Rev., 116, 1493-1518.
Phillips, N.A., 1957: A coordinate system having some special advantage for numerical forecasting. J. Meteor., 14, 184-185.
Pielke, R.A. y C.L. Martin, 1981: The derivation of a terrain following coordinate system for use in a hydrostatic model. J. Atmos. Sci., 8, 1707-1713.
Ray, P.S., Ed., 1986: Mesoscale Meteorology and Forecasting. Chapters 24-27, Amer, Meteor. Soc, 793 págs.
Staudenmaier, M.J. y J. Mittelstadt, 1997: Results of the western region evaluation of the Eta-10 model. NWS WR Tech. Attach. 97-18, 4 págs.
The COMET Program, 1993: Numerical Weather Prediction, módulo de formación en disco láser presentado por los expertos Dr. Fred Carr y Dr. Ralph Peterson.
Uccellini, L.W., D.R. Johnson y R.E. Schlesinger, 1979: An isentropic and sigma coordinate hybrid numerical model: Model development and some initial tests. J. Atmos. Sci., 36, 390-414.
Zhu, Z., J. Thuburn, B.J. Hoskins y P.H. Haynes, 1992: A vertical finite-difference scheme based on a hybrid - - p coordinate. Mon. Wea. Rev., 120, 851-862.
Resolución horizontal
Carr, F.H., 1988: Introduction to Numerical Weather Prediction Models at the National Meteorological Center. University of Oklahoma, 63 págs.
The COMET Program, 1993: Numerical Weather Prediction, módulo de formación en disco láser presentado por los expertos Dr. Fred Carr y Dr. Ralph Petersen.
Conklin, R.J., 1992: Computer models used by AFGWC and NMC for weather analysis and forecasting. AFGWC/TN 92/001, 69 págs.
DiMego, G.J., 1988: The National Meteorological Center Regional Analysis System. Mon. Wea. Rev., 116, 977-1000.
Mittelstadt, J., 1998: The Eta-32 Model. NWS WR-Technical Attachment No. 98-03.
Perkey, D.J., 1986: Formulation of mesoscale numerical models. Mesoscale Meteorology and Forecasting, P.S. Ray, Ed., Amer. Meteor. Soc., 573-596.
Staudenmaier, M. y J. Mittelstadt, 1997: Results of the Western Region evaluation of the Eta-10 modeleqn. NWS WR-Technical Attachment No. 97-18.
Resolución vertical
Derber, J.C., W-S, Wu, 1998: The use of TOVS cloud-cleared radiances in the NCEP SSI Analysis System. Mon. Wea. Rev., 126, 2287-2302.
Gallus, W.A., Jr. y J.B. Klemp, 1999: On the behavior of flow over step orography. Accepted Mon. Wea. Rev.
Hoke, J.E., N.A. Phillips, G.J. Dimego, J.J Tuccillo y J.G. Sela, 1989:The regional analysis and forecast system of the National Meteorological Center. Wea. Forecasting, 4, 323-325.
Houghton, D.D., R.A. Petersen y R. Wobus, 1993: Spatial resolution impacts on National Meteorological Center Nested Grid Model simulations. Mon. Wea. Rev., 121, 1450-1466.
Mesinger, F., T.L. Black y M.E. Baldwin, 1995: Impact of resolution and of the eta coordinate on skill of the Eta Model precipitation forecasts. Numerical Methods in Atmospheric and Oceanic Modeling: The André J. Robert Memorial Volume. C. A. Lin, Ed., need publisher, 399-423.
Morgan, M., University of Wisconsin, Personal communication.
Pecnick, M.J. y D. Keyser, 1989: The effect of spatial resolution on the simulation of upper-tropospheric frontogenesis using a sigma-coordinate primitive equation model. Meteor. Atmos. Phys., 40, 137-149.
Persson, P.O.G. y T.T. Warner, 1991: Model generation of spurious gravity waves due to inconsistency of the vertical and horizontal resolution. Mon. Wea. Rev., 119, 917-935.
Sanders, F., 1988: Life history of mobile troughs in the upper westerlies. Mon. Wea. Rev., 116, 2629-2948.
The COMET Program, 1993: Numerical Weather Prediction, módulo de formación en disco láser presentado por los expertos Dr. Fred Carr y Dr. Ralph Petersen.
Dominio y condiciones de frontera
The COMET Program, 1993: Numerical Weather Prediction, módulo de formación en disco láser presentado por los expertos Dr. Fred Carr y Dr. Ralph Petersen.
Perkey, D.J., 1986: Formulation of mesoscale numerical models. Mesoscale Meteorology and Forecasting, P.S. Ray, Ed., Amer. Meteor. Soc., 573-596.
Scott, R., R.D. Koster, D. Entekhabi y M.J. Suarez, 1995: Effect of a canopy interception reservoir on hydrological persistence in a general circulation model. J. Climate, 8, 1917-1922.
Warner, T.T., R.A. Petersen y R.E. Treadon, 1997: A tutorial on lateral boundary conditions as a basic and potentially serious limitation to regional numerical weather prediction. Bull. Amer. Met. Soc., 78, 2599-2617.
Colaboradores
Patrocinadores de COMET
The COMET® Program está patrocinado por el National Weather Service (NWS) de NOAA, con fondos adicionales de las siguientes organizaciones:
- Air Force Weather (AFW)
- Australian Bureau of Meteorology (BoM)
- European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT)
- Meteorological Service of Canada (MSC)
- National Environmental Education Foundation (NEEF)
- National Polar-orbiting Operational Environmental Satellite System (NPOESS)
- NOAA National Environmental Satellite, Data and Information Service (NESDIS)
- Naval Meteorology and Oceanography Command (NMOC)
Colaboradores del proyecto
Asesores científicos principales:
- Dr. Ralph Petersen — NOAA/NCEP/EMC (jubilado)
- Dr. William Bua — UCAR/COMET
- Dr. Stephen Jascourt — UCAR/COMET
Gerente principal del proyecto
- Dr. Gregory Byrd — UCAR/COMET
Jefes del proyecto
- Dr. William Bua — UCAR/COMET
- Dr. Stephen Jascourt — UCAR/COMET
Diseño instruccional
- Bryan Guarente — UCAR/COMET
- Tsvetomir Ross-Lazarov — UCAR/COMET
Diseño gráfico/interfaz
- Steve Deyo — UCAR/COMET
- Brannan McGill — UCAR/COMET
- Heidi Godsil — UCAR/COMET
Diseño multimedia
- David Russi — UCAR/COMET
Equipo de integración HTML de COMET, 2020
- Tim Alberta — Gerente del proyecto
- Dolores Kiessling — Jefa del proyecto
- Steve Deyo — Diseñador gráfico
- Gary Pacheco — Jefe de desarrollo web
- David Russi — Traductor
- Gretchen Williams — Desarrolladora web
- Tyler Winstead — Desarrollador web
Personal de COMET, octubre de 2009
Director
- Dr. Timothy Spangler
Subdirector
- Dr. Joe Lamos
Administración
- Elizabeth Lessard, Administración y gerencia comercial
- Lorrie Alberta
- Michelle Harrison
- Hildy Kane
Soporte de hardware/software y programación
- Tim Alberta, Gerente principal de grupo
- Bob Bubon
- James Hamm
- Ken Kim
- Mark Mulholland
- Wade Pentz, estudiante
- Jay Shollenberger, estudiante
- Malte Winkler
Diseño instruccional
- Dr. Patrick Parrish, Gerente principal de grupo
- Dr. Alan Bol
- Lon Goldstein
- Bryan Guarente
- Dra. Vickie Johnson
- Tsvetomir Ross-Lazarov
- Marianne Weingroff
Grupo de producción audiovisual
- Bruce Muller, Gerente de grupo
- Steve Deyo
- Seth Lamos
- Brannan McGill
- Dan Riter
- Carl Whitehurst
Meteorólogos/Científicos
- Dr. Greg Byrd, Gerente principal de proyectos
- Wendy Schreiber-Abshire, Gerenta principal de proyectos
- Dr. William Bua
- Patrick Dills
- Dr. Stephen Jascourt
- Matthew Kelsch
- Dolores Kiessling
- Dra. Arlene Laing
- Dra. Elizabeth Mulvihill Page
- Amy Stevermer
- Warren Rodie
- Dr. Doug Wesley
Redacción científica
- Jennifer Frazer
Traducción al español
- David Russi
NOAA/National Weather Service - Forecast Decision Training Branch
- Anthony Mostek, Jefe de la sucursal en COMET
- Dr. Richard Koehler, Jefe de entrenamiento hidrológico
- Brian Motta, Entrenamiento IFPS
- Dr. Robert Rozumalski, Coordinador de SOO Science and Training Resource (SOO/STRC)
- Ross Van Til, Meteorólogo
- Shannon White, Entrenamiento AWIPS
Meteorólogos visitantes del Servicio Meteorológico de Canadá (MSC)
- Phil Chadwick
- Jim Murtha