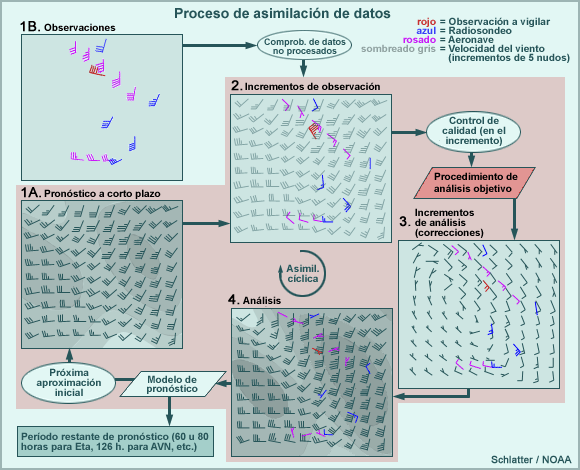
Procedimiento de análisis objetivo
Hemos llegado al NÚCLEO de la preparación del análisis para el próximo ciclo de pronóstico, la gran «caja negra» que toma los incrementos de observación de todos los diferentes tipos de observaciones, cada uno con sus propias características de error y diversas densidades de observación, y los convierte en un campo uniforme con los cambios de las variables de análisis en la malla del modelo. Esto es lo que hace 3D-VAR ahora, lo que hacía la interpolación óptima (Optimum Interpolation, OI) en el pasado y lo que harán 4D-VAR y los demás métodos que se desarrollen en el futuro. La forma exacta de hacerlo determina si:
- el análisis se parece más a las observaciones o al campo inicial;
- el análisis es desparejo o uniforme;
- se permite que una observación afecte a más de una de las variables de pronóstico de manera coherente con la física y dinámica del modelo;
- los datos se tratan de manera físicamente razonable, por ejemplo, distribuyendo el efecto de un elemento de datos individual a lo largo de las isentropas y las trayectorias y no sobre una región de forma esférica.
Aunque una discusión de los procedimientos de análisis objetivo para interpolar los incrementos de observación con la malla de pronóstico puede parecer esotérica, recuerde que de todos los elementos individuales del sistema de modelado, este proceso probablemente contribuye en mayor medida al grado de éxito (o fracaso) del pronóstico del modelo, de modo que una comprensión general de estos procedimientos complejos le permitirá interpretar la guía numérica de forma inteligente. Por supuesto que todos los elementos del sistema de modelado deben trabajar en concierto. Esencialmente, el procedimiento de análisis sopesa la evidencia.
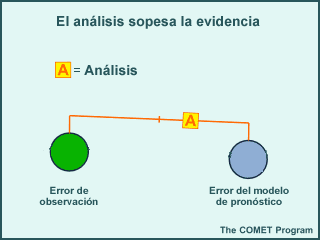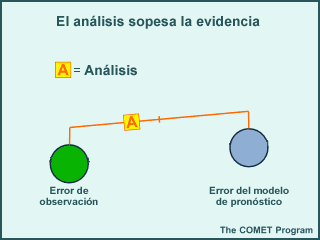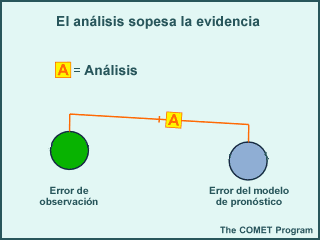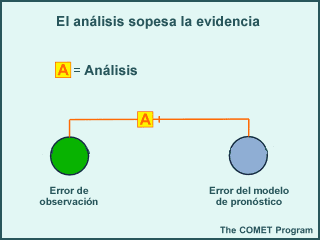
Los campos del pronóstico a corto plazo del modelo se colocan en un platillo de la balanza. El análisis debe conservar la información de coherencia física y dinámica entre las distintas variables a la vez que toma en cuenta las estructuras de error típico del modelo conocidas. Estos errores se utilizan tanto en el lugar donde se realiza la observación como en los patrones espaciales de correlación de los errores del modelo en un nivel o lugar con los de otros niveles o lugares.
De forma análoga, las observaciones ocupan en otro platillo de la balanza. El análisis trata de encajar las observaciones a la vez que toma en cuenta sus errores típicos conocidos. Como dichos errores son distintos en los diferentes sistemas de observación, el análisis puede hacer encajar mejor los tipos de observaciones que son más exactos y representativos. Los errores de observación empleados en el análisis son la suma de los errores provenientes de dos fuentes:
- el error de instrumento, que se basa en pruebas del instrumento en sí, y
- el error de representación.
Por ejemplo, cuando una radiosonda atraviesa una banda de lluvia frontal, se ve afectada por los detalles de mesoescala de dicha banda de lluvia. Como el sondeo resultante no es representativo de las estructuras resolubles por un modelo global, su uso reduciría el grado de certeza de que la temperatura media de toda una celda de malla estará dentro de determinado margen, digamos un grado, de este valor observado. Si aumentamos el error esperado a un nivel superior al que podemos atribuir al instrumento, el análisis puede tener en cuenta el menor grado de idoneidad de cualquier observación puntual para los campos de análisis de modelo. Dado que el sistema de análisis no sabe nada sobre las estructuras de pequeña escala (como una banda de lluvia individual), tiene que protegerse de esa posibilidad devaluando levemente la observación.
Estos errores de observación se comparan con los errores de fondo esperados y se utilizan juntos para decidir si es más confiable el campo de fondo o la observación, y el análisis tiende a preferir el lado cuyo error esperado es menor. El proceso de análisis empleado para hacer esta determinación se describe más a fondo en la sección Análisis, a la cual puede acceder mediante el menú de la izquierda. Debido a que los patrones de error esperados del modelo y el error de representación esperado de las observaciones deben hacer frente a una amplia gama de condiciones meteorológicas, pueden no ser apropiados para el régimen meteorológico y las observaciones individuales del día de hoy. Por lo tanto, es posible que el análisis no escoja siempre el mejor punto de equilibrio entre los campos iniciales y las observaciones. Esto puede ser particularmente importante en el caso de los eventos meteorológicos extremos que el modelo rara vez o nunca encontró antes, ya que no forman parte de las estadísticas de errores esperados.
Para conservar la estructura del campo de fondo, el procedimiento de análisis enlaza las correcciones de una variable con otra y distribuye en sentido vertical y horizontal el efecto de los cambios introducidos en una variable. Por ejemplo, los vientos en el nivel de 700 hPa pueden cambiar directamente como resultado de los incrementos de observación del viento introducidos en el nivel de 500 hPa (el efecto de la extensión de los datos en sentido vertical) y de forma indirecta debido al cambio provocado por los datos en el gradiente de temperatura en 850 hPa (relación del viento térmico). Las verdaderas relaciones dinámicas empleadas, el grado en que se imponen en los incrementos del análisis y la forma y el alcance de las funciones de influencia vertical y horizontal varían de un modelo a otro.