El desafío de las tormentas convectivas

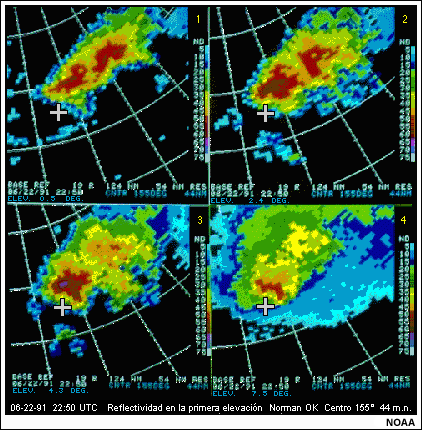
Pronosticar las tormentas convectivas es uno de los principales retos del trabajo del meteorólogo operativo. Debido a las condiciones de tiempo severo con ellas asociadas, las tormentas convectivas representan una grave amenaza, tanto para el ser humano como para sus bienes materiales. Además, debido a su tamaño pequeño y ciclo de vida corto, y a la gran variedad de formas que pueden adoptar a lo largo de su evolución, las tormentas convectivas siguen contándose entre las más difíciles de pronosticar con exactitud.

Esta lección le ayudará a elaborar una estrategia que le permita basarse en el conocimiento de las relaciones entre el entorno de la tormenta y su estructura para anticipar la estructura de las tormentas convectivas, su evolución y su potencial para provocar condiciones de tiempo severo. La capacidad de predecir las posibles estructuras de las tormentas es fundamental para poder administrar sus actividades durante un episodio de actividad convectiva. Si aprende a formular las expectativas correctas sobre lo que es posible y probable dado un entorno tormentoso en particular, se convertirá en un pronosticador más eficiente y preciso.

Descripción de la lección

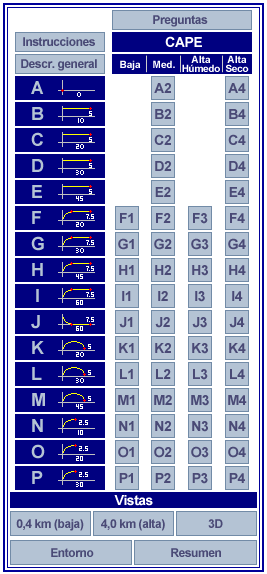
Una matriz de tormentas convectivas es un poco diferente de la mayoría de las lecciones que estamos acostumbrados a estudiar. En lugar de presentarle información para que aprenda, practique y ponga a prueba su capacidad de aplicar los conocimientos adquiridos mediante un caso de estudio centrado en una situación de pronóstico, esta matriz le permitirá «descubrir» una serie de principios que podrá luego aplicar en su trabajo.

La matriz comprende 54 simulaciones numéricas cuatridimensionales basadas en las interacciones entre 16 hodógrafas distintas y 4 perfiles termodinámicos. Al seleccionar y comparar las animaciones de estas simulaciones, podrá discernir la influencia de las variaciones en el empuje hidrostático (flotabilidad) y la cizalladura vertical del viento en la estructura y la evolución de las tormentas.

Modelos de nubes

Los modelos numéricos nos permiten aislar los efectos de ciertas cualidades individuales del entorno y descubrir determinadas relaciones de dependencia que son difíciles de observar como parte de las complejas interacciones que se producen en la naturaleza. Una matriz de tormentas convectivas pone esta potente herramienta de investigación a su alcance de modo tal que pueda descubrir tales relaciones de dependencia entre el empuje hidrostático y la cizalladura vertical del viento en relación con las tormentas convectivas de la misma forma en que las descubriría un investigador. En la sección Modelado de nubes, disponible a partir del menú principal, encontrará más detalles sobre los modelos de nubes en general y sobre los modelos de nubes específicos que se utilizaron para producir las simulaciones de esta matriz.

Una matriz de tormentas convectivas también puede servir como una herramienta de investigación y de referencia. La lección no fue diseñada para un solo uso, sino está pensada para volver a ella una y otra vez. De hecho, puede resultarle útil consultarla durante cada estación convectiva, para refrescar su entendimiento de las relaciones entre la tormenta y su entorno o incluso para obtener ideas sobre los escenarios de tormentas posibles dadas las condiciones ambientales de un día en particular.

Materiales complementarios

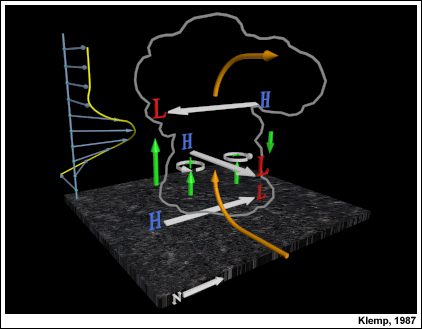
COMET ofrece varias lecciones que brindan información complementaria sobre los modelos conceptuales que describen los tipos clave de tormentas convectivas y los procesos físicos que las controlan, como las siguientes:

Principios de convección I: empuje hidrostático y CAPE
Principios de convección II: uso de la hodógrafa,
Principios de convección III: cizalladura y tormentas convectivas
Severe Convection II: Mesoscale Convective Systems.

Parte de la información que se presenta en estos materiales complementarios se encuentra convenientemente resumida en las secciones Modelos conceptuales y Procesos físicos de Una matriz de tormentas convectivas.

Ventajas del modelado de nubes

Esta lección utiliza los resultados de un modelo numérico de nubes para aclarar los procesos físicos relevantes a la evolución de las tormentas. De forma muy similar a los experimentos controlados de laboratorio, los estudios de modelado de nubes nos permiten visualizar la evolución de una tormenta sin las complejidades inherentes a la observación de las tormentas en el mundo real. Los resultados de modelado han sido extremadamente útiles para los investigadores y los teóricos, aportando nuevas perspectivas sobre los mecanismos físicos que subyacen a la gran variedad de estructuras de tormenta observadas. La matriz de tormentas convectivas demuestra que el modelado también sirve para enseñar acerca de estos mecanismos.

Verificación del modelo de nubes

• Ejemplo 1
• Ejemplo 2

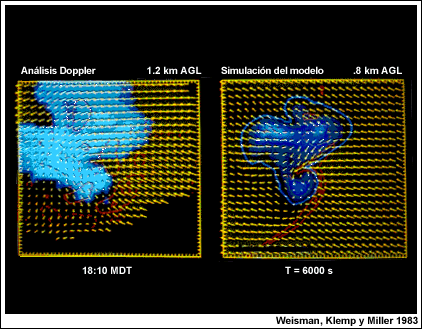
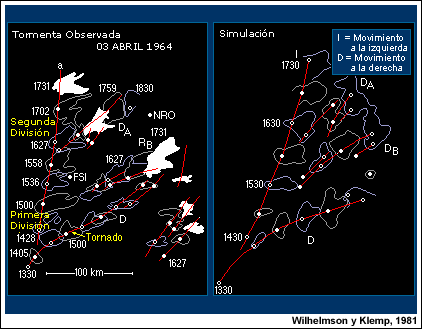
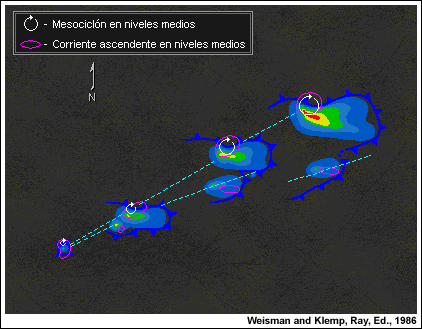
Confiamos en el uso de los resultados de modelado de nubes porque los estudios realizados con los modelos numéricos han logrado reproducir muy bien muchas de las estructuras observadas en el espectro de las tormentas convectivas. Las simulaciones numéricas son capaces de reproducir gran parte de los detalles de la estructura de las tormentas supercelulares captadas con el radar Doppler, incluso los mesociclones de niveles bajos y la estructura en forma de gancho que se observan en el campo de reflectividad del radar. El ejemplo 1, producido durante el experimento CCOPE, demuestra esta capacidad. En el ejemplo 2, una simulación numérica reproduce gran parte de la compleja evolución y el desplazamiento de las células asociadas con una tormenta, observada el 3 de abril de 1964 que se dividió. Los resultados de los modelos se utilizan teniendo presente que solo proporcionan una imagen simplificada de la atmósfera real. No obstante, sí ofrecen una sólida base a partir de la cual podemos analizar el comportamiento real de una tormenta.

Comparación de los modelos de nubes y los modelos de PNT

Los modelos de nubes difieren de los modelos de predicción numérica del tiempo (PNT) usuales: además de no ser hidrostáticos, por lo general, utilizan resoluciones horizontales inferiores a los 4 km, en tanto que los modelos de PNT son hidrostáticos y sus resoluciones horizontales superan los 20 km. A tales resoluciones, la convección se debe parametrizar, lo cual no nos permite estudiar los detalles de los procesos convectivos. En razón de los requerimientos computacionales de los modelos de malla fina, el dominio de los modelos de nubes suele ser más pequeño que el de los modelos de pronóstico, cubriendo tal vez áreas de 100 km² en lugar de áreas de 1000 km² o más. Esto dificulta la incorporación de factores de mayor escala que pueden influir en los procesos convectivos de las simulaciones en los modelos de nubes.

Las simulaciones utilizadas en esta lección se crearon con el modelo numérico de nubes Klemp-Wilhelmson, un esquema totalmente compresible, no hidrostático, diseñado para estudiar estructuras atmosféricas pequeñas con resoluciones de hasta 100 metros (Klemp y Wilhelmson, 1978).

Variables del modelo

El modelo Klemp-Wilhelmson resuelve las ecuaciones de pronóstico para las tres componentes de velocidad (u,v,w), la temperatura potencial (theta), la presión (p), un coeficiente de mezcla (km) y las relaciones de mezcla del vapor de agua (qv), del agua en la nube (qc) y del agua de lluvia (qr) . Se utiliza una parametrización Kessler para las transiciones microfísicas entre las distintas fases (o estados) del agua. No se han incluido ni los procesos del hielo ni la fuerza de Coriolis en las presentes simulaciones, ya que no producen un impacto significativo en los tipos de procesos que se examinan en la lección.

Initial Conditions

Condiciones iniciales

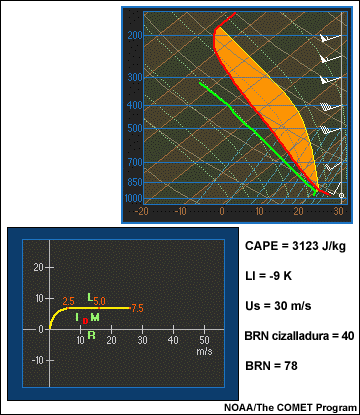
Cada simulación se ejecuta en un entorno que en un comienzo es horizontalmente homogéneo en todos los niveles y se caracteriza por un único sondeo de temperatura, humedad y vientos. En realidad, las condiciones de frontera preexistentes y las variaciones horizontales en las condiciones del entorno pueden tener un impacto significativo en la evolución de una tormenta. Aun así, las simulaciones simplificadas nos ofrecen una buena base a partir de la cual podemos intentar comprender estas interacciones más complejas.

Mecanismo de disparo de la convección

Las células convectivas se disparan utilizando una burbuja elipsoidal de aire caliente con un exceso máximo de temperatura de 2 °C en su centro. Si bien normalmente el mecanismo de disparo de las tormentas reales es un factor de mesoescala, como una zona de convergencia en niveles bajos, los estudios de modelado que utilizan estos procedimientos de inicialización más realistas no cambian las conclusiones aquí presentadas de modo significativo.

Dominio del modelo

Todas las simulaciones se corren en un dominio de 120 x 120 x 17,5 km, con una resolución horizontal de 2 km y vertical de 700 m. Esto permite estudiar las características a escala de la tormenta, tales como la estructura general de las corrientes ascendentes y descendentes, el desarrollo de los mesociclones en niveles medios y otros controles básicos del sistema tormenta-entorno asociados con la cizalladura vertical del viento y el empuje hidrostático. Sin embargo, esta resolución no alcanza para reproducir los detalles de la estructura del mesociclón en niveles bajos, incluidos los que pueden conducir a la génesis de un tornado. Algunos estudios recientes sugieren que puede ser necesaria una resolución de 100 m o menos para obtener una simulación que capture tal grado de detalle.

Estructura y evolución de las células ordinarias

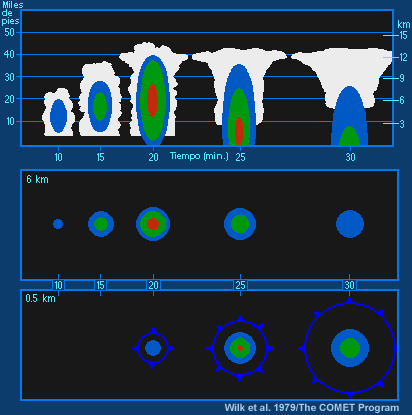
Los plazos indicados corresponden al tiempo dado en minutos en la figura.

10 minutos

Es probable que el primer eco de radar se observe poco después de que la nube haga su aparición visual. La altura del primer eco varía considerablemente en función del entorno, pero será más bajo en las áreas más húmedas.

La célula se desplazará a la misma velocidad y en la misma dirección que el viento ambiental.

15 minutos

Dado que a menudo la cizalladura vertical del viento es débil, la precipitación se forma directamente encima de la corriente ascendente, haciendo que los ecos máximos queden apilados en la vertical. Esto se puede observar en nuestro corte vertical o al comparar diferentes niveles en las presentaciones PPI del radar. En este momento la célula se compone enteramente de corriente ascendente y la totalidad del eco se localiza en altura.

20 minutos

Finalmente, cuando la precipitación se torna demasiado pesada para que la corriente ascendente la sostenga, baja hacia la superficie con la corriente descendente, en el interior de la corriente ascendente.

25 minutos

En poco tiempo la célula se compone principalmente de una corriente descendente. Cuando dicha corriente alcanza la superficie, el frente de racha asociado con la bolsa de aire frío comienza a expandirse. Es en esta etapa, cuando el núcleo de precipitación se descarga, que pueden producirse condiciones de tiempo severo, como granizo grande o vientos destructivos. Estas condiciones de tiempo severo tienden a ser de corta duración, ya que la tormenta se disipa rápidamente. Estas células ordinarias que producen estallidos de tiempo severo se denominan «tormentas pulsantes». Sin embargo, aun en las células ordinarias que producen tiempo severo el tamaño del granizo estará limitado por la intensidad de la corriente ascendente generada solamente por procesos de empuje hidrostático.

30 minutos

Conforme la célula se disipa, el frente de racha sigue alejándose en todas las direcciones del área de precipitaciones. El flujo saliente puede inducir nuevos desarrollos, dependiendo esto de la altura del nivel de convección libre (NCL), del espesor de la bolsa de aire frío, de las variaciones en la estabilidad y otros factores. Sin embargo, en la mayoría de los casos el ascenso producido por el frente de racha en condiciones de cizalladura débil resulta insuficiente, de por sí, para generar nuevas células de manera coherente. Lo más común es que algún factor externo, como la interacción con otra superficie o con el relieve topográfico, determine el lugar más probable para el desarrollo inicial de células nuevas.

La duración de las células depende de la intensidad de la corriente ascendente y de la extensión vertical de la célula. Las células poco profundas que solo incluyen procesos de lluvia cálida pueden completar su ciclo de vida entero, desde la aparición de la primera nube hasta el cese de las precipitaciones, en 20 a 30 minutos. Una célula más profunda también involucra los procesos de hielo, por lo cual la duración de su ciclo de vida puede duplicarse. Las células con más energía potencial disponible para la convección (Convective Available Potential Energy, CAPE) y, por ende, con corrientes ascendentes más intensas, durarán más, dado que pueden mantener una mayor cantidad de la precipitación en altura. En consecuencia, también será más probable que produzcan condiciones de tiempo severo en forma de tormentas pulsantes.

Simulaciones de células ordinarias

Entre las simulaciones de Una matriz de tormentas convectivas encontrará muchas células ordinarias. Algunas, como la de este ejemplo, dispararán la formación algunas otras células ordinarias a medida que su bolsa de aire frio se expande. En otros casos, aparecerán células ordinarias junto a células o sistemas más organizados. Al estudiar las simulaciones de la matriz, trate de determinar qué combinaciones de hodógrafa y CAPE producen células ordinarias.

Corte vertical de las células

Este corte vertical muestra un sistema multicelular maduro con células en distintas etapas de crecimiento. En este ejemplo, la cizalladura del entorno es unidireccional y no existen factores externos. Por lo tanto, las células y el sistema se mueven en la misma dirección, desplazándose las células a la velocidad del viento medio.

De la célula más vieja (la célula 1) solo queda un yunque, localizado a mayor distancia en el lado de proveniencia del vector cizalladura. La figura muestra, en orden hacia la derecha, otras células en etapas cada vez más tempranas de sus ciclos de vida, siendo la más joven la que se encuentra más adelante, en el lado de propagación del vector cizalladura (la célula 5).

Este patrón de evolución de las células constituye una característica distintiva de los sistemas multicelulares organizados. Las células individuales del sistema tienden a asemejarse a células ordinarias, tanto en su estructura como en su evolución.

Patrón de ecos

En la etapa presentada en este diagrama esquemático, la reflectividad más extensa se observa en la célula 3, la cual se encuentra en su fase de madurez. Las células ubicadas en el lado de propagación del vector cizalladura respecto a esta célula no muestran todavía un núcleo de reflectividad en la superficie, sino solamente en altura.

El frente de racha se extiende y se aleja del sistema multicelular en todas las direcciones. Dado que en el entorno hay algo de cizalladura en los niveles bajos, el crecimiento de células nuevas se ve favorecido en el lado de propagación del vector cizalladura respecto a la bolsa de aire frío, donde el ascenso es mayor. (Tenga presente la interacción entre los vórtices inducidos por la bolsa de aire frio y la cizalladura del viento). El corte en niveles medios muestra los ecos iniciales de las células nuevas. El alcance de su desarrollo dependerá de las características del entorno.

También pueden iniciarse células nuevas en otros puntos a lo largo del límite determinado por el flujo de aire saliente —el frente de racha—, algo que depende de factores externos. Además, si los vientos en niveles bajos son lo suficientemente fuertes, el frente de racha no se extenderá simétricamente.

Patrón del flujo

El origen de la afluencia principal de aire al sistema multicelular es el aire no perturbado que se encuentra delante de la tormenta. A medida que esta se acerca, el borde de avance de la bolsa de aire frío en expansión lo levanta. En términos relativos al sistema, dicho aire se expande desde el frente hacia atrás, de modo que para cuando el aire que asciende en la célula más nueva forma un yunque, está a cierta distancia detrás del borde de avance de la bolsa de aire frío.

Las flechas curvadas hacia abajo muestran las corrientes descendentes que se originan en los niveles medios.

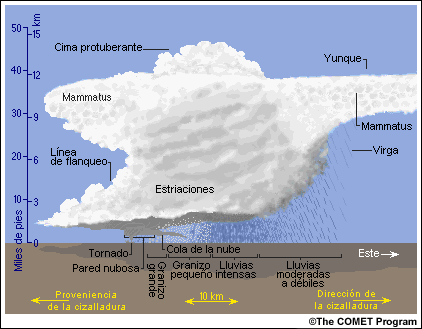
Características visibles y tiempo severo

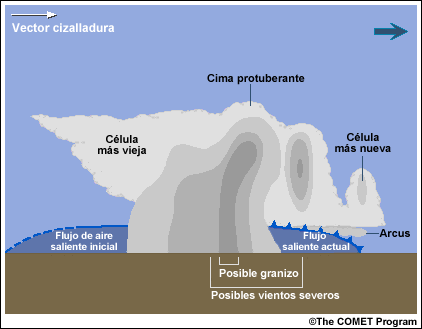
Una de las características más distintivas de las nubes de algunos sistemas multicelulares organizados es una estructura nubosa tipo arcus (en inglés: shelf cloud) bien definida que presenta una base nítida y plana, indicativa de una corriente ascendente activa. A veces, la bolsa de aire frío se adelanta a las células en desarrollo, formándose una nube arcus aparte a lo largo del borde de avance.

Los fenómenos de tiempo severo más comunes asociados a los sistemas multicelulares son los vientos intensos, el granizo y la amenaza de inundaciones (si el sistema se desplaza de forma propicia). Sin embargo, el potencial de tiempo severo se encuentra algo limitado por el hecho de que las células individuales que componen el sistema son de breve duración y tienen una estructura similar a las células ordinarias.

Simulaciones de sistemas multicelulares

Entre las simulaciones de la matriz encontrará varios sistemas multicelulares en los cuales se observa una regeneración celular continua sobre el flanco del sistema que favorece su desarrollo. Al estudiar la matriz, trate de determinar qué combinaciones de hodógrafa y CAPE producen sistemas de tormentas multicelulares.

Evolución de las supercélulas

• Introducción
• Curva en sentido horario
• Línea recta
• Curva en sentido antihorario

Cuando la cizalladura vertical del viento ambiental es lo suficientemente fuerte, las estructuras de la supercélula pueden comenzar a evolucionar, ya sea individualmente o como parte de un sistema convectivo más grande, como por ejemplo una línea de turbonada. Pueden formarse una gran variedad de tipos y evoluciones de supercélulas, en función de la forma de la hodógrafa y otras características del entorno.

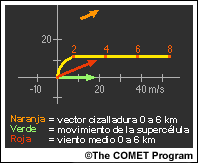
Si la hodógrafa curva en sentido horario (el vector cizalladura traza una curva hacia la derecha con la altura), cuando el sistema se divide el miembro que se desplaza hacia la derecha tiene mayores probabilidades de mantener su estructura supercelular que el que se desplaza hacia la izquierda. La mitad izquierda del sistema puede convertirse en una supercélula débil, en un sistema multicelular o, si la curva de la hodógrafa es muy pronunciada, puede simplemente disiparse.

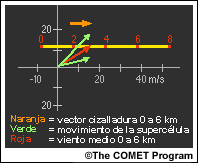
Si la magnitud de la cizalladura vertical del viento es suficiente y la hodógrafa es recta, la célula inicial puede dividirse en dos supercélulas. Debido a las fuerzas de presión que actúan en ambos flancos de la célula original, la supercélula ciclónica sale de la hodógrafa y se aleja hacia la derecha respecto del vector cizalladura media del viento, en tanto que la supercélula anticiclónica se desplaza hacia la izquierda.

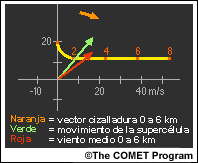
Si la hodógrafa curva en sentido antihorario (el vector cizalladura gira hacia la izquierda con la altura), cuando el sistema se divide el miembro que se desplaza hacia la izquierda resulta favorecido.

Vista plana de una supercélula

• Diagrama
• Tiempo severo

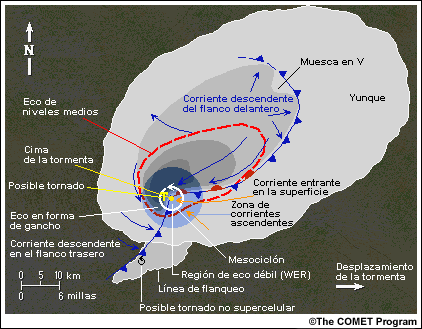
Esta representación esquemática de una clásica tormenta supercelular madura con movimiento hacia la derecha muestra el contorno de la nube y la distribución de la precipitación en niveles bajos, es decir, el patrón de reflectividad. La línea de trazos rojos representa el eco de 30 dBZ en niveles medios y el punto amarillo indica la ubicación del tope de la tormenta. La flecha circular indica la posición del mesociclón en niveles medios, en tanto que las flechas alargadas indican el ingreso y egreso del aire en los niveles bajos. También se muestran los límites de los flujos de aire saliente generados por la tormenta. Se supone que la tormenta se desplaza hacia el este.

Línea de flanqueo

Normalmente, el ascenso que se produce en el borde de avance de la corriente descendente del flanco trasero crea una línea de torrecúmulos llamada línea de flanqueo. Con el tiempo, algunas de estas células pueden desarrollarse y fusionarse con la tormenta principal.

Región de eco débil

La presencia de un eco en los niveles medios que sobresale y se extiende a buena distancia hacia el sur, por encima del eco en forma de gancho, indica la proximidad de una fuerte corriente ascendente y un mesociclón en los niveles medios. En el radar, la precipitación sostenida en altura produce una región de eco débil (weak echo region o WER). Una corriente ascendente muy fuerte puede producir un «hoyo» de reflectividad rodeado por valores de reflectividad altos. Esta estructura se conoce como «región de eco débil acotada» (bounded weak echo region o BWER).

Patrón de flujo

Las abundantes precipitaciones que ocurren en el flanco delantero de la tormenta producen la extensa área de flujo saliente, aire que es enfriado por la lluvia, conocida como la corriente descendente del flanco delantero. También hay una corriente descendente en el flanco trasero, causada por la precipitación concentrada en la parte trasera de la tormenta por el mesociclón. Gran parte del aire que alimenta la tormenta proviene de la dirección de propagación y no fluye a través del aire de la corriente descendente. Esto permite que la corriente ascendente, que comprende principalmente aire inestable del entorno, permanezca sin diluir. Sin embargo, parte del aire que ingresa al sistema también proviene de la región de la corriente descendente del flanco delantero, importante para el desarrollo de la rotación en los niveles bajos.

Eco en forma de gancho

Es evidente un gradiente de reflectividad muy marcado en niveles bajos (en el lado sur de esta tormenta), una señal de que la corriente ascendente es muy fuerte. El mesociclón ha concentrado la precipitación en la parte trasera de la corriente ascendente. Esto da lugar al característico eco en forma de gancho, situado en la parte sudoeste de esta tormenta en particular, que se desplaza hacia el este. El mesociclón en sí está ubicado en la muesca del eco en forma de gancho.

Tiempo severo

Es consabido que las supercélulas presentan varios tipos de amenazas de tiempo severo. Dada la intensidad de sus corrientes ascendentes, estas tormentas suelen producir granizo grande. Cuando se desplazan lentamente, estas tormentas, que tienen una vida prolongada, también pueden provocar inundaciones. Si bien no todas las tormentas supercelulares engendran tornados, ciertos estudios han demostrado que la mayoría de los tornados fuertes y violentos ocurren en relación con estas tormentas organizadas, que incluyen mesociclones intensos y fuerte baroclinicidad en los niveles bajos, dos aspectos que pueden ser factores contribuyentes importantes en la génesis de los tornados. Aunque no se muestran en esta figura esquemática, los vientos severos en línea recta son otra posible manifestación de las tormentas supercelulares.

Corte vertical de una supercélula

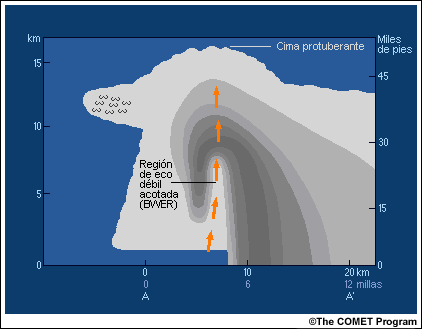
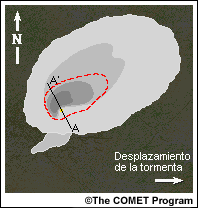
En este corte vertical de una supercélula madura se observa una región de eco débil acotada (BWER). El marcado gradiente de intensidad de la precipitación se extiende hacia arriba, hasta alcanzar los niveles medios, a lo largo del borde de la corriente ascendente. La corriente ascendente es vertical, pese a la fuerte cizalladura del viento (indicada por la expansión de la precipitación y el yunque), una indicación de que la corriente ascendente es sumamente fuerte.

Variaciones de las supercélulas

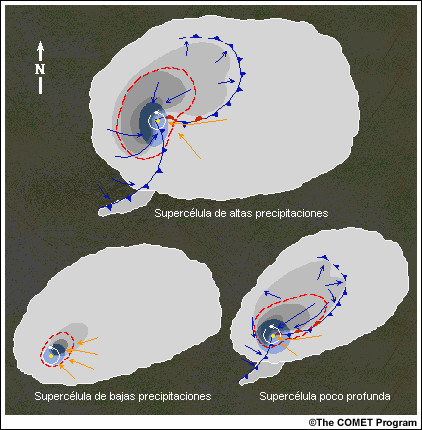
Se han identificado muchas variantes de la estructura «clásica» de las supercélulas, como las supercélulas de alta precipitación, las supercélulas de baja precipitación y las supercélulas poco profundas o «minisupercélulas». Se están realizando investigaciones adicionales para ayudar a los científicos y a los pronosticadores a comprender mejor estas variantes. Es probable que vea algunas de estas estructuras supercelulares alternativas en algunas de las simulaciones de la matriz.

Simulaciones de supercélulas

Al estudiar las simulaciones de la matriz, encontrará muchos ejemplos de tormentas que se propagan alejándose del viento medio, que exhiben mesociclones en niveles medios y que muestran patrones de eco en forma de gancho. Al explorar la matriz, trate de determinar qué combinaciones de hodógrafa y CAPE producen estos resultados. Además, examine las hodógrafas para tratar de predecir los diversos tipos de evolución: las divisiones simétricas y las que favorecen el desarrollo de la supercélula de la derecha o de la izquierda.

Clasificación de las tormentas convectivas

Si bien puede resultar útil clasificar las tormentas en tipos generales de acuerdo con sus características estructurales, esto también puede inducir a error. En la naturaleza, las tormentas no siempre encajan perfectamente en tales categorías, ya que, por el contrario, se distribuyen a lo largo de un espectro y a menudo exhiben las características de varios tipos de tormentas durante sus respectivos ciclos de vida y hasta pueden modularse mutuamente. Por esta razón es más importante comprender y categorizar los procesos físicos que determinan las estructuras de las tormentas. Si comprendemos cuáles son los entornos que presentan mayores probabilidades de producir los diversos procesos de desarrollo de las tormentas, podemos aumentar nuestra capacidad de anticipar una gama de estructuras posibles. Con ello adquirimos mayor destreza en términos de anticipar situaciones específicas de tiempo severo.

La importancia de la cizalladura vertical del viento (observaciones)

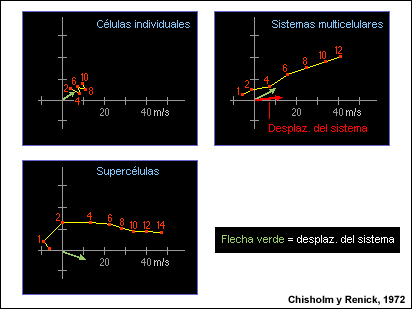
Si bien al principio los procesos de empuje hidrostático son los más importantes para la existencia de la convección, la cizalladura vertical del viento juega un rol primordial en el control de la estructura y la evolución de una tormenta. Esto se sabe gracias a numerosos estudios de observación y de modelado que muestran que la organización y la longevidad de las tormentas y los sistemas convectivos aumentan con la magnitud de la cizalladura vertical de viento.

Por ejemplo, los resultados del estudio de las tormentas de granizo en Canadá realizado por Chisolm y Renick que se presentan en esta figura permiten observar una relación entre las células ordinarias de breve duración y los entornos con poca cizalladura del viento, entre los sistemas multicelulares y los entornos con valores medianos de cizalladura, y entre las supercélulas y las magnitudes de cizalladura vertical más altas. Las hodógrafas que se muestran en la figura se componen de los datos de numerosos casos de estudio.

La importancia de la cizalladura vertical del viento (estudios de modelado)

Los estudios conceptuales de modelado numérico también reproducen estas relaciones de dependencia con la cizalladura, tal como se observa en este montaje de simulaciones de tormentas correspondientes a varios perfiles de cizalladura vertical.

Estas simulaciones revelan que tanto la magnitud de la cizalladura vertical del viento como la profundidad y la forma del perfil de la cizalladura pueden afectar considerablemente al comportamiento de la tormenta.

El número de Richardson (BRN)

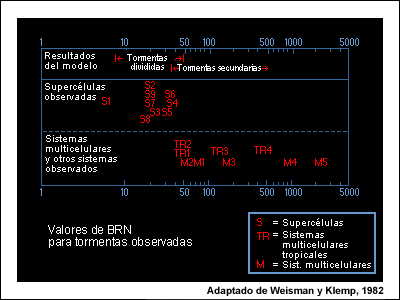
Las relaciones entre la cizalladura y el empuje hidrostático pueden representarse por medio de un parámetro conocido como número de Richardson (bulk Richardson number, BRN).* Este diagrama resume los valores de BRN propicios para distintos tipos de tormentas, tanto para un estudio de modelado como para un conjunto de casos observados. Nótese que en este estudio los valores bajos de BRN (indicativos de fuerte cizalladura vertical del viento en relación con el empuje hidrostático) están mayormente asociados a las supercélulas (tormentas divididas), mientras que los valores altos se relacionan con los sistemas multicelulares (formados por células ordinarias).

*El número de Richardson se calcula dividiendo la CAPE entre la cizalladura, donde la cizalladura se define como la mitad del cuadrado del vector diferencia entre el viento medio en la capa 0 a 6 km y un viento representativo de la capa de superficie.

Tres procesos físicos determinantes

Simplificaremos los procesos físicos primarios que controlan las tormentas convectivas de acuerdo con tres categorías: los procesos de empuje hidrostático, las interacciones entre la bolsa de aire frío y la cizalladura, y las interacciones entre la corriente ascendente y la cizalladura. Las pestañas siguientes se limitan a ofrecer una breve descripción de estas tres categorías, pero encontrará una descripción más profunda de cada una de ellas en su respectiva sección.

Las tormentas arquetípicas, como las células ordinarias, las multicélulas y las supercélulas, surgen naturalmente de combinaciones particulares de esos procesos físicos básicos. Las descripciones de estos tipos de tormentas se presentan en la sección Modelos conceptuales.

• Procesos de empuje hidrostático
• Bolsa de aire frío/cizalladura
• Corriente ascendente/cizalladura

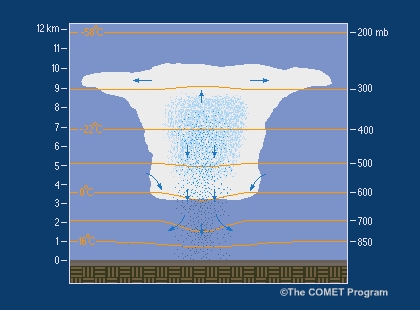
Los procesos de empuje hidrostático controlan la convección en el nivel más fundamental, ya que el empuje hidrostático está directamente relacionado con la fuerza de las corrientes convectivas ascendentes y descendentes.

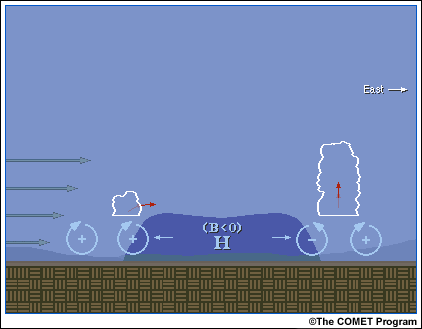
Las interacciones entre la bolsa de aire frío y la cizalladura vertical del viento revelan cómo el flujo de aire saliente generado por la tormenta puede crear nuevas células convectivas dadas diferencias en la magnitud de la cizalladura vertical del viento en niveles bajos y en la circulación generada por la bolsa de aire frío. Estos procesos son críticos para el desarrollo de los sistemas multicelulares de larga duración.

Las interacciones entre la corriente ascendente y la cizalladura vertical del viento conducen a una variedad de efectos importantes para la evolución de las tormentas, como la generación de la rotación en los niveles medios, un factor esencial en la producción de las tormentas supercelulares.

Previsión de los procesos de convección

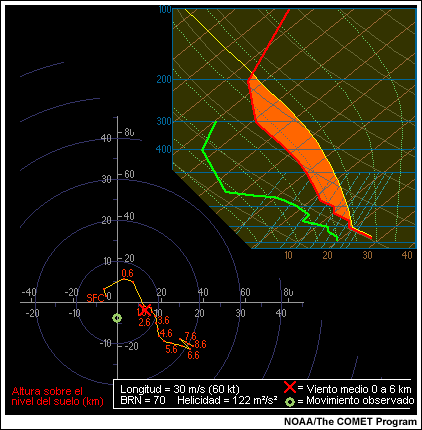
Para anticipar estos procesos, el pronosticador debe evaluar no solo un conjunto de índices útiles, como la CAPE, el BRN y la Us (magnitud de la cizalladura), sino también examinar directamente los perfiles termodinámicos y las hodógrafas. Una matriz de tormentas convectivas ilustra la importancia de usar tanto los parámetros como los diagramas a la hora de anticipar la estructura de una tormenta.

Evolución completa de una célula ordinaria

Esta animación del ciclo de vida de una célula ordinaria que evoluciona en un entorno sin cizalladura vertical del viento ilustra esquemáticamente los procesos básicos asociados con el empuje hidrostático en el interior de una tormenta convectiva.

Las páginas siguientes examinan estos procesos paso a paso.

Evolución inicial de la corriente ascendente

En un entorno inestable, una vez que el aire se eleve hasta alcanzar su nivel de convección libre (NCL) continuará ascendiendo en tanto siga siendo más cálido que el aire que lo circunda.

Evolución ulterior de la corriente ascendente

En determinado momento la burbuja alcanza el nivel al cual su temperatura iguala la de su entorno, que se conoce como nivel de equilibrio (NE). Debido a que posee un cierto impulso ascensional, que depende de la intensidad de la corriente ascendente, la burbuja experimenta un leve ascenso adicional, más allá del de nivel de equilibrio, y esto produce la cima protuberante sobre el yunque. Finalmente, como la burbuja es más fría que su entorno, se hunde y regresa a su nivel de equilibrio, donde oscila alrededor del mismo.

Desde abajo continúan ascendiendo nuevas burbujas de aire, por lo cual el aire sigue esparciéndose en la cima de la tormenta, formando un yunque más grande.

Mientras todo esto sucede, la humedad se condensa en la corriente de aire ascendente. El peso de las partículas de precipitación aumenta hasta que la corriente ascendente ya no pueda sostenerlas en altura, y entonces comienzan a caer nuevamente sobre la corriente ascendente.

Continuación de la evolución

El efecto inicial de la precipitación es arrastrar el aire hacia abajo, como muestran las flechas en esta animación, que cambian de dirección, de arriba a abajo, a medida que la precipitación desciende hacia el suelo.

El efecto de arrastre e incorporación de aire más seco en los niveles medios y la evaporación que ocurre a medida que la lluvia cae debajo de la base de la nube contribuyen a reducir la temperatura de la corriente descendente hasta que, una vez más fría que el aire circundante, aumenta su aceleración descendente.

Algunos estudios han demostrado que gran parte del aire de la corriente descendente se origina en los niveles medios de la tormenta, por lo general a entre 3 y 5 km sobre el nivel del suelo. 

La corriente descendente

Cuando la corriente descendente alcanza la superficie, se esparce y forma la bolsa de aire frío. La corriente descendente y la bolsa de aire frío en expansión representan las etapas finales del ciclo de vida de la célula.

Diagramas termodinámicos

Los diagramas termodinámicos, como el diagrama oblicuo T-log p (o diagrama de Herlofson), constituyen la mejor herramienta para que el pronosticador pueda anticipar la fuerza potencial de los procesos de empuje hidrostáticos. Siguiendo las curvas apropiadas del diagrama que representan los procesos termodinámicos de las burbujas durante sus movimientos ascendentes y descendentes, el pronosticador puede estimar la intensidad potencial de las corrientes ascendentes y descendentes de una célula convectiva.

CAPE

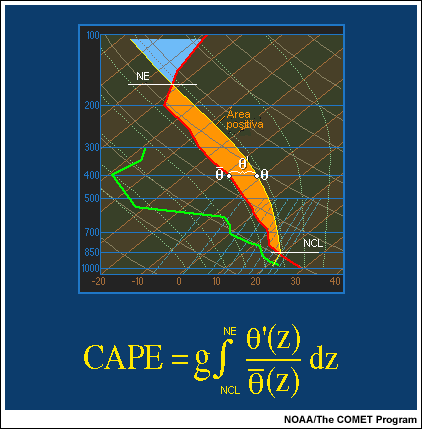
Las corrientes ascendentes se pueden estimar calculando el área positiva en el diagrama termodinámico, que da una medida de la diferencia entre la temperatura potencial de la burbuja que asciende y su entorno. La medida cuantitativa de dicha área positiva es la energía potencial convectiva disponible o CAPE (convective available potential energy).

Los programas de sondeo calculan la CAPE en forma cuantitativa mediante la ecuación que se muestra en la figura.

Vorticidad generada por la bolsa de aire frío

La bolsa de aire frío expansiva generada por una tormenta convectiva se puede describir ya sea en términos de presiones más altas producidas hidrostáticamente dentro del aire frío, o bien en términos de la circulación que este genera en su borde de avance. La ecuación de la vorticidad horizontal establece que la vorticidad horizontal, o circulación, se genera dondequiera que existan gradientes horizontales de empuje hidrostático. De modo particular, en el ejemplo aquí ilustrado se genera vorticidad horizontal negativa a lo largo del borde derecho (al este) de la bolsa de aire frío, mientras que se genera vorticidad horizontal positiva a lo largo del borde izquierdo (al oeste) de la misma.

La circulación existente en el borde de avance de la bolsa de aire frío tiende a extraer el aire frío desde la superficie, al tiempo que tiende a levantar el aire caliente del entorno por encima del borde de avance del aire frío.

Si el ascenso generado por la bolsa de aire frío es suficiente como para elevar el aire hasta el nivel de convección libre (NCL), entonces podrá desencadenarse convección nueva. Sin embargo, a menudo la altura del NLC excede el espesor de la bolsa de aire frío, y en este caso el ascenso que esta produce resulta, de por sí, insuficiente para disparar nuevas tormentas.

Vorticidad del entorno

Cuando el perfil vertical del viento presenta cizalladura, el entorno también incluye vorticidad horizontal. Podemos visualizar esta vorticidad si imaginamos una rueda de paletas orientada en sentido paralelo a la dirección de la cizalladura. Tenga presente que la rueda de paletas no es sino una herramienta para visualizar la vorticidad y que en la realidad el aire del entorno no rota alrededor de un eje horizontal.

Interacción entre vórtices

En un entorno con cizalladura vertical del viento en niveles bajos (en este ejemplo, la velocidad de los vientos del oeste aumenta con la altura), podemos interpretar la cizalladura como una capa de vorticidad horizontal positiva. En el lado de proveniencia del vector cizalladura (que en este ejemplo es el lado izquierdo), dicha vorticidad se orienta en la misma dirección que la vorticidad generada por la bolsa de aire frío. La influencia de la suma de las dos zonas de vorticidad aumenta la velocidad de arrastre del aire, que sube y luego vuelve a caer sobre la bolsa de aire, produciendo de este modo un ascenso neto mínimo.

En el lado de propagación del vector cizalladura, en cambio, la vorticidad horizontal asociada con la cizalladura del entorno está orientada en sentido opuesto a la vorticidad generada por la bolsa de aire frío. La influencia de estas dos fuentes de vorticidad sumadas produce un chorro con una orientación más vertical en el borde de avance de la bolsa de aire frío, creando un ascenso más profundo en este lado.

Con frecuencia, el ascenso más profundo que ocurre en el lado de propagación del vector cizalladura respecto a la bolsa de aire frío en expansión es suficiente como para transportar el aire a una buena altura por encima de la bolsa de aire frío, lo que facilita el disparo de la convección, aun cuando el nivel de convección libre sea relativamente alto. Este mayor ascenso en entornos con cizalladura vertical es el motivo principal del patrón de continua regeneración de células que se observa en los sistemas multicelulares de larga duración.

Inclinación de la tormenta

Una corriente ascendente convectiva puede verse afectada de varias maneras mientras crece en un entorno con cizalladura vertical del viento. Quizás la más simple de observar sea la tendencia de una nube convectiva a inclinarse en la dirección del vector cizalladura vertical del viento. Esto ocurre cuando la columna de aire ascendente bloquea parcialmente el aire del entorno, produciendo presiones relativamente altas en el lado de proveniencia del vector cizalladura y presiones relativamente bajas en el lado de propagación del mismo. Este gradiente de presión horizontal causa la inclinación de las burbujas ascendentes en la dirección del vector cizalladura. Este efecto, producto de la cizalladura vertical del viento, distribuye la precipitación en el lado de propagación del vector cizalladura respecto a la corriente ascendente y su impacto en el ciclo de vida total de la tormenta es mínimo.

Sin embargo, la cizalladura vertical del viento tiene un impacto más significativo en la corriente convectiva ascendente en términos de generar la rotación en niveles medios. En entornos con cizalladura fuerte, esto puede conducir a la formación de tormentas supercelulares de larga duración.

Líneas de vórtice

La línea de vórtice es una herramienta sumamente útil para interpretar la forma en que las interacciones entre la corriente ascendente y la cizalladura vertical del viento generan rotación en los niveles medios. Podemos representar con un vector vorticidad la magnitud y orientación de la vorticidad horizontal presente en un entorno con cizalladura vertical. La dirección de dicho vector vorticidad indica el eje de rotación, mientras su longitud representa la magnitud. Si dibujamos una línea a través de una serie de vectores vorticidad adyacentes, obtendremos una «línea de vórtice» (el vector azul largo en la animación de la derecha). Si bien la vorticidad existe en toda la capa de cizalladura, nuestro interés se centra principalmente en la vorticidad horizontal en los niveles bajos.

Retroalimentación dinámica entre la corriente ascendente y la cizalladura

Dado que las líneas de vórtice conservan su sentido de rotación aun cuando las distorsione el flujo, podemos utilizarlas para observar la manera en que una tormenta en desarrollo genera rotación en los niveles medios. En el caso que aquí se presenta, la cizalladura es unidireccional (es decir: una hodógrafa recta), por lo cual los centros de rotación en desarrollo exhiben simetría axial.

En la etapa 1, en un comienzo la corriente ascendente inclina las líneas de vórtice hacia la vertical, creando una pareja de vórtices, uno ciclónico y otro anticiclónico, en los niveles medios. Para esta escala de movimiento atmosférico, tanto la rotación ciclónica como la anticiclónica están asociadas a presiones relativas más bajas. Por lo tanto, se genera una presión más baja con cada vórtice en niveles medios, lo cual crea un gradiente de presión vertical orientado hacia arriba en estos lugares.

Dinámica de las hodógrafas con curva en sentido horario

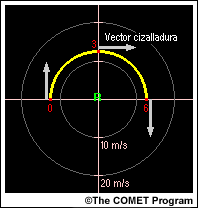
Si bien en la naturaleza se pueden observar hodógrafas rectas y supercélulas divididas simétricas, son más comunes las hodógrafas curvadas en sentido horario. Cuando la hodógrafa se curva en sentido horario (es decir, el vector cizalladura gira hacia la derecha con la altura, como en la hodógrafa y el diagrama aquí ilustrados), el gradiente de presión horizontal entre la región de presiones relativamente altas y la de presiones relativamente bajas que provoca la inclinación de la tormenta se curva también en sentido horario con la altura. Esta orientación genera un gradiente de presión vertical más intenso dirigido hacia arriba sobre el flanco derecho de la tormenta, que está asociado con el centro de rotación ciclónica en niveles medios.

En el flanco opuesto de la tormenta (que en este caso es el lado izquierdo de la cizalladura media del viento), la orientación del gradiente de presión vertical tiende a disminuir el movimiento ascendente. Por lo tanto, este mecanismo no solo estimula la corriente ascendente en uno de los flancos de la tormenta, sino que, a la vez, inhibe el crecimiento de una corriente ascendente en el lado opuesto. En el caso de una hodógrafa curvada en sentido horario, esto hace que la célula ciclónica del flanco derecho sea más dominante que la célula anticiclónica del flanco izquierdo.

En este caso, la supercélula ciclónica se propaga hasta salir de la hodógrafa y hacia la derecha del vector cizalladura media de viento, cerca del centro de la curva de la hodógrafa.

En los entornos de cizalladura muy fuerte y curvada en sentido horario, la corriente ascendente del flanco izquierdo puede simplemente disiparse, sin que llegue a aparecer una célula aparte.

Dinámica de las hodógrafas con curva en sentido antihorario

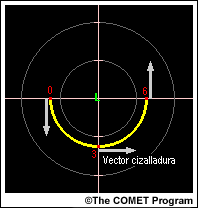
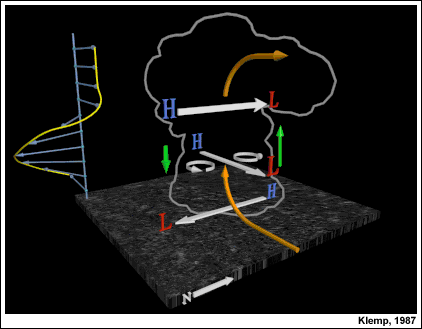
De forma análoga, cuando la hodógrafa gira en sentido antihorario (hacia la izquierda) con la altura, el que dominará será el miembro anticiclónico, izquierdo, de la tormenta dividida.

En este caso, la supercélula anticiclónica se propaga hasta salir de la hodógrafa, hacia la izquierda del vector cizalladura media de viento, cerca del centro de la curva de la hodógrafa.

Debido al efecto de Coriolis, que tiende a producir curvaturas en sentido horario en niveles bajos (por ejemplo: la espiral de Ekman), las hodógrafas con giro antihorario no están favorecidas climatológicamente en el hemisferio norte. Sin embargo, todos los mecanismos necesarios para producir supercélulas potentes son posibles siempre que la cizalladura media del viento sea lo suficientemente fuerte, de modo que es importante no poner demasiado énfasis en una hodógrafa con giro horario como único elemento predictor de tormentas supercelulares.

Rotación en niveles bajos

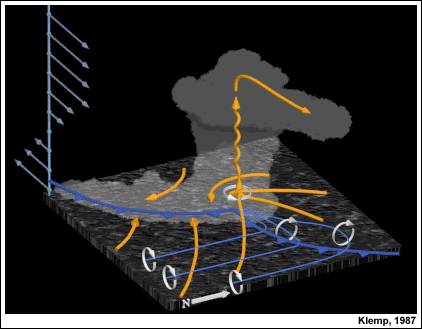
La generación de la rotación en niveles bajos es un resultado adicional de los procesos que acabamos de describir. Esta representación tridimensional muestra una supercélula clásica en su etapa madura. Las líneas de vórtice cerca de la superficie (en azul) representan la vorticidad del entorno curvada hacia la corriente ascendente de la tormenta, en la zona baroclínica de la corriente descendente del flanco delantero. Esto indica una generación baroclínica de vorticidad horizontal en esta zona. Una vez que penetre la corriente ascendente, dicha vorticidad se alarga en la vertical para crear una rotación mucho más intensa en los niveles bajos. Este proceso es un factor importante que contribuye a la rotación en niveles bajos y puede conducir a la génesis de un tornado.

La matriz de tormentas convectivas

Bibliografía

Andra, D.L., Jr., 1993: Observations of an anticyclonically rotating severe storm. Preprints, 17th Conf. on Severe Local Storms, St. Louis, MO, Amer. Meteor. Soc., 186--190.

Bluestein, H.B. y C.R. Parks, 1983: A synoptic and photographic climatology of low-precipitation severe thunderstorms in the southern plains. Mon. Wea. Rev., 111, 2034--2046.

Bluestein, H.B. y G.R. Woodall, 1990: Doppler radar analysis of a low-precipitation severe storm. Mon. Wea. Rev., 118, 1640--1664.

Brooks, H.E. y R.B. Wilhelmson, 1993: Hodograph curvature and updraft intensity in numerically modeled supercells. J. Atmos. Sci., 50, 1824--1833.

Brooks, H.E., C.A. Doswell III y L.J. Wicker, 1993: STORMTIPE: A forecasting experiment using a three-dimensional cloud model. Wea. Forecasting, 8, 352--362.

Brown, R.A., 1990: Characteristics of supercell hodographs. Preprints, 16th Conf. on Severe Local Storms, Kananaskis Park, Alta., Canada, Amer. Meteor. Soc., 30--33.

Brown, R.A. y V.T. Wood, 1991: On the interpretation of single-Doppler velocity patterns within severe thunderstorms. Wea. Forecasting, 6, 32--48.

Burgess, D.W. y L.R. Lemon, 1990: Severe thunderstorm detection by radar. Radar in Meteorology, D. Atlas ed., Amer. Meteor. Soc., 619--647.

Chisholm, A.J. y J.H. Renick, 1972: The kinematics of multicell and supercell Alberta hailstorms. Alberta Hail Studies, Research Council of Alberta Hail Studies, Rep. 72-2, Edmonton, Canada, 24--31.

Davies-Jones, R., 1984: Streamwise vorticity: The origin of updraft rotation in supercell storms. J. Atmos. Sci., 41, 2991--3006.

Doswell, C.A., III, 1985: The operational meteorology of convective weather. Volume II: Storm scale analysis. Memorándum técnico de la NOAA. ERL ESG-15, 240 págs.

Doswell, C.A., III, 1991: A review for forecasters on the application of hodographs to forecasting severe thunderstorms. Natl. Wea. Dig., 16 (1), 2--16.

Doswell, C.A., III, A.R. Moller y R. Przybylinski, 1990: A unified set of conceptual models for variations on the supercell theme. Preprints, 16th Conf. on Severe Local Storms, Kananaskis Park, Alta., Canada, Amer. Meteor. Soc., 40--45.

Doswell, C.A., III, M.E. Splitt and M. Kay, 1992: On storm motion and operational assessment of supercell storm potential using hodographs. Preprints, 4th AES/CMOS Workshop on Operational Meteorology, Whistler, B.C., Atmos. Env. Serv./Can. Met. and Ocean. Soc., 245--252.

Droegemeier, K.K., S.M. Lazarus y R. Davies-Jones, 1993: The influence of helicity on numerically simulated convective storms. Mon. Wea. Rev., 121, 2005--2029.

Fankhauser, J.C. y C.G. Mohr, 1977: Some correlations between various sounding parameters and hailstorm characteristics in northeast Colorado. Preprints, 10th Conf. on Severe Local Storms, Omaha, NE, Amer. Meteor. Soc., 218--225.

Foster, M.P., A.R. Moller, L.J. Wicker y L. Cantrell, 1995: The rapid evolution of a tornadic small supercell; observations and simulation. Preprints, 14th Conf. on Weather Analysis and Forecasting, Dallas, TX, Amer. Meteor. Soc., 323--328.

Johns, R.H. y C.A. Doswell III, 1992: Severe local storm forecasting. Wea. Forecasting, 7, 588--612.

Klemp, J.B., 1987: Dynamics of tornadic thunderstorms. Ann. Rev. Fluid Mech., 19, 369--402.

Lemon, L.R., 1980: Severe thunderstorm radar identification techniques and warning criteria. Memorándum técnico de la NOAA. NWS NSSFC-3, 60 págs.

Lemon, L.R., R.J. Donaldson, D.W. Burgess y R.A. Brown, 1977: Doppler radar application to severe thunderstorm study and potential real-time warning. Bull. Amer. Meteor. Soc., 58, 1187--1193.

Marwitz, J.D., 1972a: The structure and motion of severe hailstorms. Part I: Supercell storms. J. Appl. Meteor., 11, 166--179.

Marwitz, J.D., 1972b: The structure and motion of severe hailstorms. Part II: Multi-cell storms. J. Appl. Meteor., 11, 180--188.

Marwitz, J.D., 1972c: The structure and motion of severe hailstorms. Part III: Severely sheared storms. J. Appl. Meteor., 11, 189--201.

Moller, A.R., C.A. Doswell III y R. Przybylinski, 1990: High-precipitation supercells: A conceptual model and documentation. Preprints, 16th Conf. on Severe Local Storms, Kananaskis Park, Alta., Canada, Amer. Meteor. Soc., 52--57.

Moller, A.R., C.A. Doswell III, M.P. Foster y G.R. Woodall, 1994: The operational recognition of supercell thunderstorm environments and storm structures. Wea. Forecasting, 9, 327--347.

NOAA, National Weather Service, 1991: Basic Convection I: A Review of Atmospheric Thermodynamics. Operational Support Facility/Operations Training Branch Workbook, 74 págs.

NOAA, National Weather Service, 1993: Basic Convection II. Operational Support Facility/Operations Training Branch Workbook, 43 págs.

Thunderstorm Structure and Evolution Part One. Operational Support Facility/Operations Training Branch Workbook with accompanying video tape of same name, 83 págs.

Przybylinski, R.W., T.J. Shea, D.L. Ferry, E.H. Goetsch, R.R. Czys y N.E. Wescott, 1993: Doppler radar observations of high-precipitation supercells over the mid-Mississippi Valley region. Preprints, 17th Conf. on Severe Local Storms, St. Louis, MO, Amer. Meteor. Soc., 158--163.

Rotunno, R., 1993: Supercell thunderstorm modeling and theory. Geo. Monograph 79, 57--73.

Rotunno, R. and J.B. Klemp, 1982: The influence of the shear-induced pressure gradient on thunderstorm motion. Mon. Wea. Rev., 110,136--151.

Rotunno, R. and J. Klemp, 1985: On the rotation and propagation of simulated supercell thunderstorms. J. Atmos. Sci., 42, 271--292.

Vasiloff, S.V., E.A. Brandes, R.P. Davies-Jones y P.S. Ray, 1986: An investigation of the transition from multicell to supercell storms. J. Climate and Appl. Meteor., 25, 1022--1036.

Weisman, M. L., 1996: On the use of vertical wind shear versus helicity in interpreting supercell dynamics. Preprints, 18th Conf. on Severe Local Storms, San Francisco, CA, Amer. Meteor. Soc., 200--204.

Weisman, M. L. y J. B. Klemp, 1982: The dependence of numerically simulated convective storms on vertical wind shear and buoyancy. Mon. Wea. Rev., 110, 504--520.

Weisman, M. L. y J. B. Klemp, 1984: The structure and classification of numerically simulated convective storms in directionally varying wind shears. Mon. Wea. Rev., 112, 2479--2498.

Weisman, M. L. y H.B. Bluestein, 1985: Dynamics of numerically simulated LP storms. Preprints, 14th Conf. on Severe Local Storms, Indianapolis, IN, Amer. Meteor. Soc., 167--170.

Weisman, M. L. y J. B. Klemp, 1986: Characteristics of isolated convective storms. Mesoscale Meteorology and Forecasting, P.S. Ray ed., Amer. Meteor. Soc., 331--358.

Weisman, M. L., J. B. Klemp y L.J. Miller: Modeling and Doppler analysis of the CCOPE August 2 supercell-storm. Preprints, 13th Conf. on Severe Local Storms, Tulsa, OK, Amer. Meteor. Soc., 223--226.

Weisman, M. L., J. B. Klemp y J. W. Wilson, 1983: Dynamic interpretation of notches, WERS, and mesocyclones simulated in a numerical cloud model. Preprints, 21st Conf. on Radar Meteorology, Edmonton, Alta., Canada, Amer. Meteor. Soc., 39--43.

Wilhelmson, R.B. y J.B. Klemp, 1981: A three-dimensional numerical simulation of splitting severe storms on 3 April 1964. J. Atmos. Sci., 38, 1581--1600.

Wilk, K.E., L.R. Lemon y D.W. Burgess, 1979: Interpretation of radar echoes from severe thunderstorms: A series of illustrations with extended captions. Prepared for training FAA ARTCC coordinators, National Severe Storms Laboratory, Norman, OK [se puede solicitar directamente a los autores], 55 págs.

Estrategia de aprendizaje

Cuando resulte práctico, el descubrimiento de la información puede ser una estrategia de aprendizaje más efectiva que su mera lectura. A través del aprendizaje por descubrimiento, cada persona tiene la oportunidad de conectar libremente los distintos tipos de información y construir los conocimientos de formas individualmente significativas. La lección Una matriz de tormentas convectivas, que fue creado con esta estrategia en mente, le permitirá descubrir los efectos de las relaciones de dependencia entre el empuje hidrostático y la cizalladura vertical del viento en la estructura de las tormentas convectivas. Para guiarle en este proceso, la lección ofrece una lista de preguntas y actividades. A medida que complete las tareas, las relaciones más importantes serán aparentes en la matriz. El Dr. Morris Weisman contesta todas las preguntas de la matriz y sintetiza su propia interpretación de cada una de las simulaciones en resúmenes que están disponibles una vez que se contesten todas las preguntas.

Una matriz de tormentas convectivas es un recurso de aprendizaje que también se propone ser una herramienta de referencia. La lección no fue diseñada para un solo uso, sino está pensada para volver a consultarla una y otra vez. Considere la posibilidad de volver a ella a lo largo de la estación convectiva para refrescar su entendimiento de las relaciones entre la tormenta y su entorno e incluso para obtener sugerencias sobre los escenarios de pronóstico que son posibles dadas las condiciones ambientales de un día en particular.

Lo que aprenderá de esta lección depende enteramente de usted. Recomendamos que gestione su propio proceso de aprendizaje formulándose continuamente preguntas como estas:

• ¿Tiene sentido esto?
• ¿Estoy de acuerdo con esta conclusión?
• ¿He encontrado algo similar en el pasado?

Si desea ampliar sus conocimientos sobre la estructura y la evolución de las tormentas convectivas, consulte estas lecciones de COMET:

• Principios de convección I: empuje hidrostático y CAPE
• Principios de convección II: uso de la hodógrafa
• Principios de convección III: cizalladura y tormentas convectivas
• Severe Convection II: Mesoscale Convective Systems.

Estas lecciones forman parte de un curso en línea llamado Summer Severe Weather, sobre el tiempo severo de verano, que se puede consultar en https://www.meted.ucar.edu/training_course.php?id=2.

Colaboradores

Patrocinadores de COMET

The COMET^® Program está patrocinado por el National Weather Service (NWS) de NOAA, con fondos adicionales de las siguientes organizaciones:

• Bureau of Meteorology of Australia
• Bureau of Reclamation (United States Department of the Interior)
• European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT)
• Meteorological Service of Canada (MSC)
• NOAA National Environmental Satellite, Data and Information Service (NESDIS)
• Naval Meteorology and Oceanography Command (NMOC)

Colaboradores del proyecto

Asesor científico principal

• Dr. Morris Weisman — National Center for Atmospheric Research (NCAR)

Asesoría científica adicional

• Steve Keighton — NWS
• Ed Szoke — NCAR

Meteoróloga de COMET

• Wendy Schreiber-Abshire — UCAR/COMET

Jefe del proyecto/Diseño instruccional

• Patrick Parrish — UCAR/COMET

Diseño multimedia

• Eileen Kuo — UCAR/COMET
• Carl Whitehurst — UCAR/COMET

Datos cortesía de:

• National Oceanic and Atmospheric Administration (NOAA)
• NCAR Mesoscale and Microscale Meteorology Division (MMM)

Recopilación de datos

• Steve Keighton — NWS
• David Maggert — UCAR/COMET
• Pat Parrish — UCAR/COMET
• Wendy Schreiber-Abshire — UCAR/COMET
• Ed Szoke — NCAR
• Dr. Morris Weisman — NCAR
• Amy Wyatt — UCAR/COMET (contratista)

Asistencia con la recopilación de datos

• John Clyne — NCAR/SCD
• Bill Hibbard — Space Science and Engineering Center (SSEC), University of Wisconsin-Madison
• Don Middleton-Link — NCAR/SCD
• NCAR Scientific Computing Division (SCD)
• Brian Paul — SSEC, University of Wisconsin-Madison

Fuentes de materiales gráficos adicionales

• American Meteorological Society
• Annual Review Inc.
• Department of Commerce
• Dr. David Blanchard — Fotógrafo
• Dr. Morris Weisman
• Mr. Ed Szoke — Fotógrafo
• National Oceanic and Atmospheric Administration
• National Weather Service
• Research Council of Alberta

Diseño multimedia adicional

• Patrick Parrish — UCAR/COMET
• Dennis Ward — UCAR/COMET

Infografía y animaciones

• Steve Deyo — UCAR/COMET
• Heidi Godsil — UCAR/COMET
• Julee Syverson — UCAR/COMET

Software Vis5D

• University of Wisconsin-Madison Space Science and Engineering Center (SSEC) Visualization Project

Soporte de hardware/software y programación

• Lara Ferraro — UCAR/COMET
• Susan Jesuroga — UCAR/COMET

Pruebas de software y control de la calidad

• Mike Smith — UCAR/COMET

Redacción y corrección

• Patrick Parrish — UCAR/COMET
• Wendy Schreiber-Abshire — UCAR/COMET

Redacción y corrección adicional

• Kay Levesque — UCAR/COMET

Traducción al español

Personal de COMET, otoño/invierno de 2013-2014

Director

• Dr. Rich Jeffries

Subdirector

• Dr. Greg Byrd

Administración comercial

• Elizabeth Lessard, gerenta comercial
• Lorrie Alberta, administradora
• Hildy Kane, asistenta administrativa

Servicios de tecnología de la información

• Tim Alberta, gerente de grupo
• Bob Bubon,  administrador de sistemas
• Malte Winkler, ingeniero de software

Servicios instruccionales y multimedia

• Bruce Muller, gerente de grupo
• Dr. Alan Bol, científico/diseñador instruccional
• Steve Deyo, diseñador gráfico/3D
• Lon Goldstein, diseñador instruccional
• Bryan Guarente, diseñador instruccional
• Dan Riter, ingeniero de software
• Tsvetomir Ross-Lazarov, diseñador instruccional
• David Russi, traductor de español
• Marianne Weingroff, diseñadora instruccional

Grupo científico

• Wendy Schreiber-Abshire, gerenta de grupo
• Dr. William Bua, meteorólogo
• Patrick Dills, meteorólogo
• Matthew Kelsch, hidrometeorólogo
• Dra. Elizabeth Mulvihill Page, meteoróloga
• Amy Stevermer, meteoróloga

Meteorólogos visitantes del Servicio Meteorológico de Canadá (MSC)

• Brad Snyder, contacto MSC/COMET
• Nicolas Major, contacto MSC/COMET