The Quasi-geostrophic (QG) Omega Equation represents a method for diagnosing mid-latitude synoptic-scale vertical motion at a specified time. In the absence of diabatic processes, it implies that vertical motion can be calculated from a series of geopotential height analyses at different pressure levels. It is a powerful conceptual tool for meteorologists because its terms are straightforward to interpret physically. With practice, the conclusions can easily be applied to real-time MSLP/Thickness and Geopotential Height/Temperature analyses.
The adiabatic form of the QG Omega Equation (QGOE) is presented below:
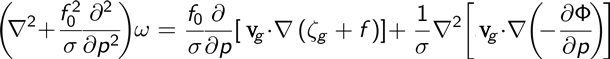
This QG omega equation learning tool is based on a simple, two-level model of the atmosphere in the mid-latitudes and is based on the methods found in T.N. Carlson's "Mid-Latitude Weather Systems" on pages 268-275 or in J. Holton's "An Introduction to Dynamic Meteorology" on pages 166-170.
This widget enables the user to visually interpret the mathematical terms in this equation.
The left-hand side (LHS) term is very similar to the 3-D laplacian of omega. It is commonplace to assume the dominant mode of vertical motion is sinusoidal: approximately zero at both the surface and tropopause, and attaining a maximum/minimum value in the mid-troposphere. Under these circumstances, the LHS differential operator behaves qualitatively like a minus sign.
The first right-hand side (RHS) term represents differential absolute vorticity advection.
The second RHS term is proportional to the horizontal laplacian of horizontal temperature advection.
It is important to note that the omega equation is of diagnostic use only. It reveals the omega distribution at the time of a specified geopotential height analysis. However, as there are no time derivatives, it does not predict future vertical motion.
This tool evaluates the omega field associated with a simple two-level model of the troposphere.
The 1000hPa height distribution is specified and is sinusoidal in x and y. This represents an idealised wave-train of circular High and Low pressure systems, with wavelength 4000km.
The thermal distribution is represented by the 1000-500hPa thickness where the direction of isotherms is assumed to be constant with height. The user can specify either a zonal thickness pattern, or a sinusoidal thickness pattern whose position relative to the 1000hPa pattern can be varied.
The 500 hPa height distribution is determined from the 1000hPa height and 1000-500hPa thickness.
The omega distribution is presented at 500 hPa.
These levels were chosen so that forecasters could conceptualise actual omega distributions on the basis of a quick inspection of MSLP/Thickness or 500hPa Geopotential Height/Temperature charts.
The omega distribution will change depending upon the offset of the 1000hPa and thickness fields that is selected by the user.
The impact of the RHS forcing terms can be visualised separately and overlaid to assess their contribution to the total vertical motion.
In this learning tool, we will assume that both the 500hPa height and 1000-500hPa thickness pattern behave like sinusoidal waves. Depending on the phase of the 500hPa height and 1000-500hPa thickness patterns with each other, the omega pattern will intensify or weaken. Explore the relationship between 500hPa heights, 1000-500hPa thickness and their relation to omega.