Produced by The COMET® Program
Force

Tsunamis surge ashore with incredible power and force. The waves can easily float cars, knock down buildings and people, and cause massive destruction. But how do we estimate a tsunami's force?

Force can thought of as the amount of "push" or "pull" necessary for an object to be moved.

To move something big, like a house, would take a lot of force. Tsunamis can have that much force, and more.
Dynamic vs. Hydrostatic Force

Tsunami waves can be incredibly destructive--taking lives and devastating communities near the coasts. Tsunamis move at about 48 kilometers per hour, or 30 miles per hour, as they come ashore. Part of their strength relates to the dynamic force of the wave—the force you feel standing on a beach as an ordinary wind wave pushes against your legs.
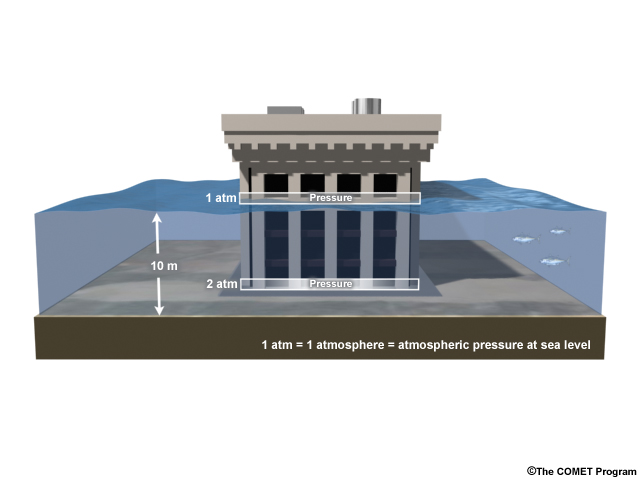
Waves also exert a second kind of force. This is called hydrostatic pressure, which is the force you feel on your ears due to the weight of the water when swimming at the bottom of a pool. If a deep wave strikes a building, the pressure at the bottom of the water is greater than at the top, and the lower floor experiences extra force. The differences add up quickly: if the wave is 10 meters high, the hydrostatic force is twice as much at the bottom of the water as it is at the top.
Buoyancy and Funneling

There are other ways waves can exert force and damage structures. Water might rise up under a building or car and lift it, an effect called the buoyancy force.

An advancing or retreating wave will carry floating debris that pushes or pulls on objects in its path and does more damage than water alone. The force of a wave might also scour or erode soil and undermine foundations, causing buildings, bridges, or seawalls to collapse.

A wave that wraps around a building may be more forceful on the back than the front because the water is funneled between buildings into smaller, more powerful streams that wrap around and meet. Think of how the water is channeled to the edge of the street toward storm drains after a rain storm.

This water becomes deeper and faster-flowing than in the center of the road. People who try to hide behind houses during a tsunami are in extra danger from this effect.
Estimating Force
Newton's 2nd Law of Motion:
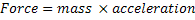
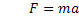
Newton's Second Law of Motion says that force equals mass times acceleration. Using that relationship, one way of approximating the force of a tsunami as it washes onto shore would be to know the mass of any and all objects it moves on the shore, and how fast it got each and every one of those objects moving.
But then we'd also have to account for other forces in the balance, like gravity and buoyancy. Is it starting to seem really complicated? Yes, it sure is.
We could instead try to approximate the mass of the water lifted by an undersea earthquake, along with its rate of lift, to estimate the force when the tsunami was created. But none of these approximations of force gives us straightforward methods for understanding the tsunami's actual power when it reaches shore.
Momentum

A different way to understand how much strength a tsunami might have as it washes onto shore would be to consider the tsunami's momentum.
Momentum can be thought of as the power of a moving object. It provides a measure of how difficult something is to stop.
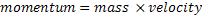
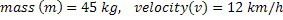
Momentum can be calculated as mass times velocity. Let's say you run across a playing field. You will have a mass (let's say 45 kg) and a speed or velocity (let's say 12 km/h).
Because the metric unit for momentum is kilogram meters per second we'll convert the velocity from kilometers per hour to meters per second:
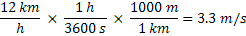
Then, multiplying the mass (45 kilograms) times the velocity (3.3 meters per second), we can calculate the momentum as 150 kilograms per meter per second:
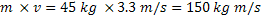
Question
If you run faster, will you change your momentum? (Choose the best answer.)
The correct answer is b).
Yes, increase your velocity and you will increase your momentum.
Relative Momentum
![]()
Momentum equals mass times velocity so a large mass moving at a high velocity has a large momentum. Slow the velocity, and the momentum will be smaller. Keep the same velocity but shrink the mass, and the momentum also becomes smaller. Let's think about what that might mean.
Question
Sort these choices according to the amount of momentum you think they have, from least to greatest. You do not have to calculate the actual momentums. Just remember that small masses moving slowly have the smallest amount of momentum, while big masses moving quickly have the largest amount of momentum. Which has the larger mass, a train locomotive or a car? Which can move faster, a toddler or a football player? Use these considerations to rank the objects from "1" (least momentum) to "4" (greatest momentum).
How did you do in estimating the order? If you picked the toddler as having the smallest mass and slowest speed, so therefore the least momentum, that's a great start. Likewise, a train locomotive would be much more massive than a car, so even if it moves at a similar speed, we expect its momentum would also be greater. The correct order, from least momentum to greatest, is Toddler, Football Player, Car, Locomotive. If we have actual values for mass and velocity, calculating momentum is simply a matter of multiplying.
Toddler (mass 13.5 kg, velocity 0.80 m/s)
![]()
Football player (mass 113 kg, velocity 3.0 m/s)
![]()
Car (mass 2000 kg, velocity 48 km/h or 13 m/s)
![]()
Freight train locomotive (mass 190,000 kg, velocity 48 km/h or 13 m/s)
![]()
Water vs. Wind

What about a 2-meter (6-ft) tsunami wave? What about a 160-km/h (100-mph) wind? Which has the larger momentum? How do they compare to the momentum of the freight train?
The momentum of the wind and the tsunami are a bit more difficult to calculate, but you already know something about the mass of water versus the mass of air. Think about two identical milk jugs, one filled with water, and one with air. The mass of the water is higher, would you agree?
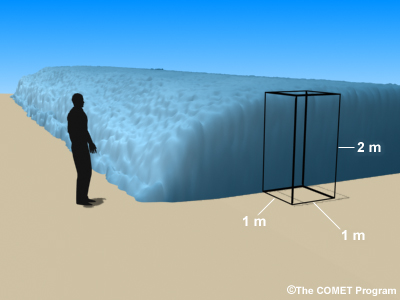
Let's take a 1 meter by 1 meter by 2 meter volume of water to approximate the front edge of a tsunami wave as it might strike a person and estimate the tsunami's momentum. Then we'll also use the mass of air associated with that same volume to estimate the wind's momentum.
First, we have to understand the relation between mass and volume. The amount of mass that fits within a given space or volume is determined by the density. Density is a substance's mass divided by its volume. If we rearrange the equation, we find that mass equals density times volume. Different substances have different densities.
We can look up the densities of water and air online or in a book.
Average density of ocean water = 1021.1 kg/m3
Average density of air = 1.22 kg/m3
The first step in calculating the mass of the leading edge of tsunami is to compute the volume (in this case 2 cubic meters). Then, we multiply the density (in the case of water, 1021.1 kg per cubic meter) times the volume to calculate mass in kilograms.
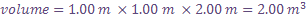
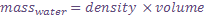
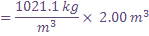
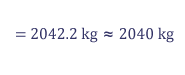
Likewise, the mass of the air is the air's volume multiplied by its density.
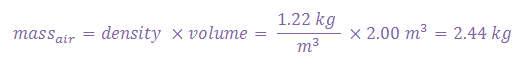
Now recall that the tsunami has a velocity of 48 km/h while the wind has a velocity of 160 km/h.
Velocity of tsunami = 48 km/h
Velocity of wind = 160 km/h
Question
Given these numbers, which has the larger momentum, a 160-km/h (100-mph) wind or a 2-m (6-ft) high tsunami? (Choose the best answer.)
The correct answer is b).
Momentum of first 2 m3 of wind equals approximately 390 kg m/s
Momentum of first 2 m3 of tsunami is greater than 98,000 kg m/s
Momentum of locomotive equals approximately 2.5 million kg m/s
The wind has a momentum of approximately 390 kg m/s, while the tsunami has a momentum of over 98,000 kg m/s. The huge difference is due to high density of water—nearly 1000 times greater than the density of air. Although the wind is moving more than three times faster than the tsunami, the water has so much more mass than the air that the tsunami's momentum becomes much, much higher than that of the wind.
Note that the momentum of a tsunami wave is still much less than that of a locomotive moving at the same speed, although we did not consider the full mass of water beyond the leading edge of the wave.

If a tsunami packs over 98,000 kg m/s of momentum into just the first one-meter length, we should definitely be aware that the entire wave—which extends for hundreds of meters beyond that leading edge--is capable of doing large amounts of damage. And a tsunami often shows up as more than a single wave—no wonder the damage can be so immense!
Immensity of Destruction

Images from the recent tsunami event in Japan clearly show the incredible momentum of tsunami waves. And those waves didn't just impact one meter of coastline—they came ashore along an area more than 2000 kilometers in length, and in some places the waves were up to ten meters high.

One scientist likened the tsunami to "one cubic kilometer" of water coming onshore.
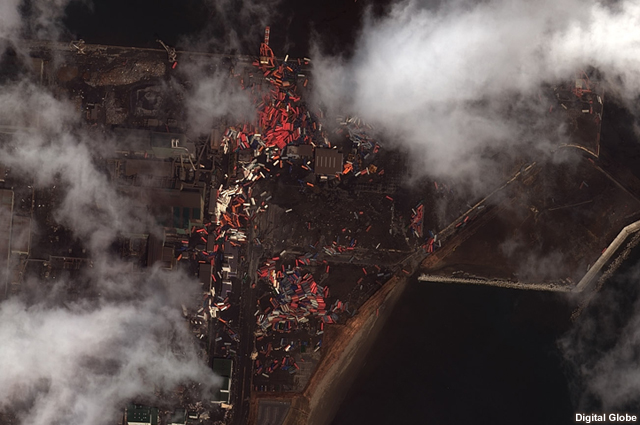
Using what you've learned in this lesson, you could estimate the momentum associated with all that water. The number would be staggering, much like the magnitude of the damage done to communities all along the shoreline is staggering to think about.
Summary
Force is the amount of push or pull necessary for an object to be moved. From Newton’s Second Law of Motion, force equals mass times acceleration.
Tsunami waves have a dynamic force, corresponding to horizontal motion, and a hydrostatic force related to water pressure. Water also provides a buoyancy force that can lift or float objects.
Calculating the force of a tsunami is difficult. Instead, we can learn something about a tsunami’s strength by estimating its momentum, which is a product of mass and velocity.
An object’s mass equals the object’s density times the volume. Different substances (such as water and air) have different densities.
If we estimate a volume of water for some part of an incoming wave, we can calculate the mass and use the tsunami’s speed to compute momentum.
Water has a high density, especially compared to air, so the momentum of even just the front edge of a tsunami wave can be very large—larger than a car traveling at the same speed and much larger than a wind blowing more than three times as fast.
Click here to return to the 4.5 Hours Page.
