Introduction
Importance du cisaillement
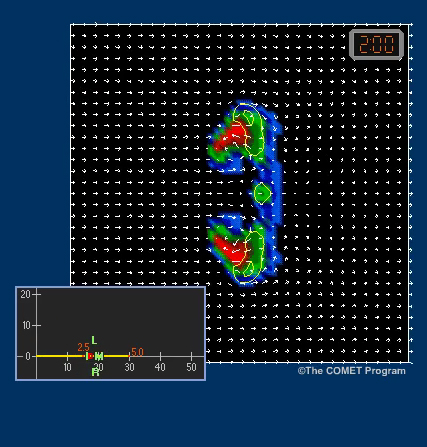
L’hodographe est un outil graphique qui aide les prévisionnistes à évaluer le cisaillement vertical du vent. Dans un environnement convectif, il est extrêmement important de comprendre le cisaillement vertical du vent afin d’anticiper le type de tempête convective, la possibilité que de nouvelles tempêtes telles que les supercellules se forment, leurs emplacements ainsi que le déplacement des tempêtes et des systèmes de tempêtes. Par exemple, ces figures illustrent les échos radar simulés pour une série de tempêtes modélisées qui ont évolué dans des conditions de cisaillement vertical du vent différentes. Ces conditions sont représentées par des hodographes idéalisés dans le coin inférieur gauche.
L’hodographe
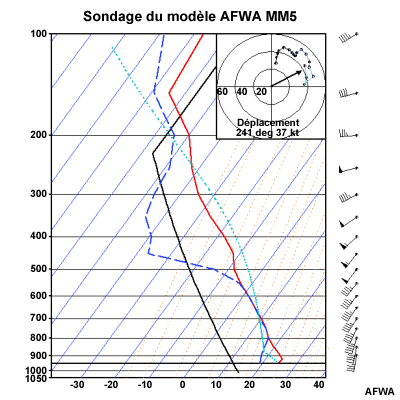
La capacité de prévoir les structures possibles de tempête est essentielle dans la gestion de vos activités, avant et pendant un événement convectif. En effet, le fait de savoir à quoi s’attendre pour un environnement de tempête donné, fera de vous un prévisionniste plus efficace et plus précis. L’hodographe illustre le cisaillement du vent dans l’environnement, celui-ci a une profonde influence sur l’évolution de la tempête. Par conséquent, un hodographe représentatif combiné à un profil de flottabilité représentatif peut considérablement améliorer l’exactitude des prévisions. Cette figure montre le sondage d’un modèle AFWA MM5, ainsi que l’hodographe associé, téléchargés à partir du site Web JAAWIN (Joint Army-Air Force Weather Information Network). Des représentations graphiques similaires de sondages et d’hodographes sont disponibles à partir de nombreuses sources.
Au terme du présent module, vous devriez comprendre comment les hodographes sont construits et comment ils peuvent vous aider à estimer le cisaillement total, le cisaillement moyen, et le vent moyen. Pour apprendre davantage sur le cisaillement et son influence sur le développement des tempêtes convectives, consultez le module complémentaire Principes de la convection III : Cisaillement et tempêtes convectives.
Représentation graphique d’un hodographe
Barbules de vent et vecteurs vent
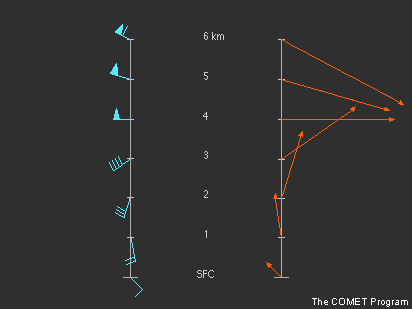
Les météorologistes connaissent bien le profil du vent vertical classique obtenu à partir d’un radiosondage qui utilise des barbules pour indiquer la direction et la vitesse du vent à différents niveaux. L’hodographe fournit les mêmes renseignements. Cependant, étant donné que son objectif principal est de montrer le cisaillement vertical du vent, l’hodographe s’appuie sur les vecteurs vent. Contrairement à une barbule, un vecteur indique la vitesse du vent par sa longueur et non par la combinaison de barbules.
Graphique à coordonnées polaires
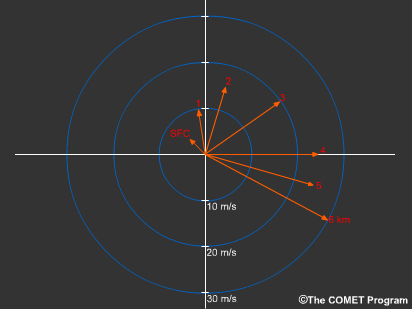
Sur un hodographe, les vecteurs vent sont indiqués sur un graphique à coordonnées polaires. Les axes du graphique représentent les quatre points cardinaux. Tous les vecteurs vent s’étendent à partir du point d’origine et dans la direction du mouvement du vent. Étant donné que la longueur des vecteurs indique la vitesse, les cercles concentriques tracés autour du point d’origine représentent les vitesses constantes du vent. Par exemple, cet hodographe indique que les vents à 4 km et à 5 km sont tous les deux de 25 m/s, alors que leurs directions respectives sont ouest et ouest-nord-ouest.
L’hodographe
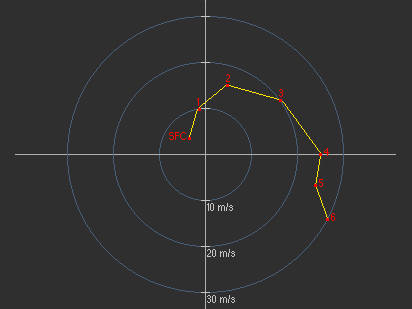
En règle générale, les vecteurs vent réels ne sont pas tracés sur l’hodographe, mais seules leurs extrémités sont indiquées sur le graphique à coordonnées polaires. On trace l’hodographe en connectant les extrémités de chaque vecteur vent.
Cisaillement vertical du vent
Vecteur de cisaillement vertical du vent
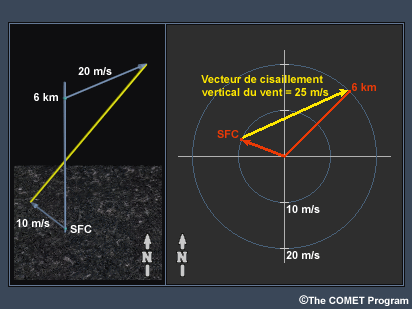
Le cisaillement vertical du vent est une description de la façon dont la vitesse du vent horizontal change en fonction de l’altitude. Le vent est une grandeur vectorielle; autrement dit, il comprend à la fois une vitesse et une direction. Par conséquent, nous pourrons déterminer le cisaillement vertical du vent en mesurant la différence vectorielle du vent horizontal à deux niveaux.
Le vecteur en résultant est appelé le vecteur de cisaillement vertical du vent. Nous décrivons ici le vecteur de cisaillement en mètres par seconde (m/s) ou en nœuds sur la profondeur de la couche qu’il représente (par exemple, 25 m/s sur 6 km). Plus précisément, le cisaillement du vent est présenté sous la forme d’une unité de distance, pour laquelle l’ampleur du vecteur de cisaillement est divisée par la profondeur de la couche. Par conséquent, 25 m/s divisé par 6 000 m (6 km) correspond à une ampleur du cisaillement de 0,004 par seconde.
Affichage du cisaillement vertical du vent
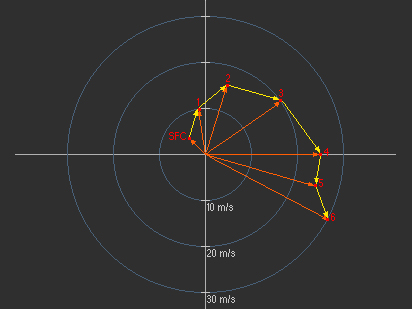
L’hodographe est parfaitement adapté pour l’affichage du cisaillement vertical du vent. À l’aide d’un graphique à coordonnées polaires, on indique le cisaillement en dessinant des vecteurs de cisaillement à partir des extrémités de chaque vecteur vent par ordre croissant d’altitude. Vous pouvez voir que les segments sur l’hodographe typique représentent en fait le cisaillement vertical du vent de chaque couche.
Si les vecteurs vent sur un hodographe représentent les vents à intervalles égaux (habituellement chaque kilomètre ou 500 m), les vecteurs de cisaillement sont équivalents en ce qui a trait à la profondeur qu’ils représentent. Leurs longueurs relatives indiquent donc la force relative du cisaillement du vent d’une couche à l’autre.
Estimation de l’ampleur du cisaillement de la couche
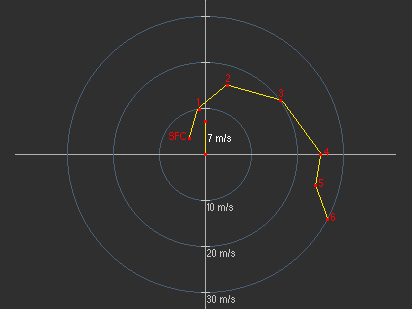
Le cisaillement vertical total du vent sur une certaine profondeur constitue un facteur important pour prévoir la structure et l’évolution de possibles tempêtes. Par conséquent, il est important de mesurer le cisaillement vertical total du vent d’une manière ou d’une autre.
Vous pouvez commencer par estimer la longueur de chaque vecteur de cisaillement. Pour ce faire, vous n’avez qu’à visuellement les comparer à l’échelle de l’un des axes. Par ailleurs, vous pouvez mesurer la longueur du vecteur et la comparer manuellement aux unités de l’échelle indiquées sur un axe.
Estimation de l’ampleur du cisaillement total
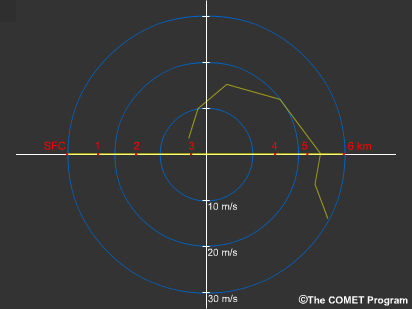
L’estimation du cisaillement vertical total du vent s’effectue en combinant les longueurs de tous les vecteurs de cisaillement sur une certaine profondeur (la longueur nette de l’hodographe).
Dans cet exemple, le cisaillement total serait de 60 m/s sur 6 km (20 000 pi).
Difficultés liées à l’estimation de l’ampleur du cisaillement
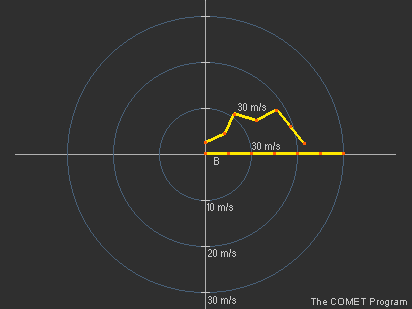
Parfois, il peut être difficile d’estimer visuellement la longueur de l’hodographe en raison d’une forme complexe. Dans de telles circonstances, le cisaillement total calculé par ordinateur peut être plus précis qu’une estimation visuelle.
Distribution du cisaillement
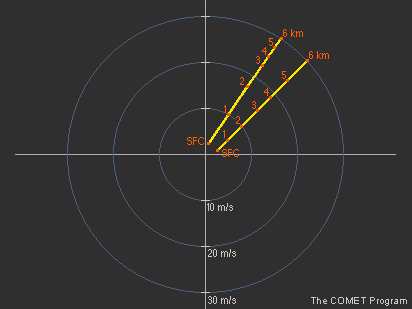
Il est également important d’étudier de quelle manière le cisaillement du vent est réparti sur la profondeur de l’hodographe. Un hodographe qui présente un fort cisaillement dans les bas niveaux a des répercussions très différentes sur la structure de la tempête qu’un hodographe avec le même niveau de cisaillement total, mais peu de cisaillement dans les bas niveaux.
Vecteur de cisaillement du vent moyen
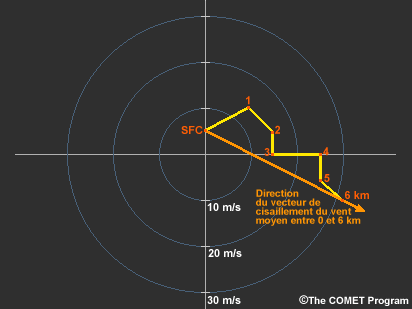
Le vecteur de cisaillement du vent moyen constitue un autre aspect important de l’environnement de la tempête qui est plus facile à percevoir sur un hodographe que par l’entremise d’autres données. Par exemple, la direction du vecteur de cisaillement moyen fournit des renseignements qui vous aident à prévoir le déplacement d’une supercellule.
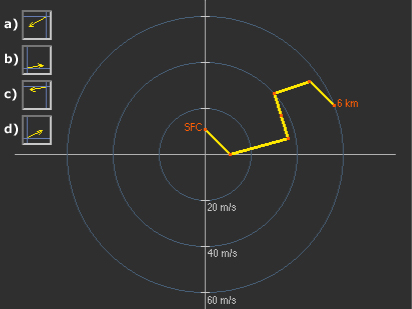
Vous pouvez déterminer la direction du cisaillement du vent moyen (mais pas l’ampleur) simplement en traçant une ligne à partir du point qui indique le vent de surface jusqu’au point indiquant le vent à 6 km (20 000 pi). Encore une fois, nous utilisons la couche comprise entre 0 et 6 km comme étant la couche ayant le plus d’influence sur la tempête.
En profondeur : Calcul du vecteur de cisaillement du vent moyen
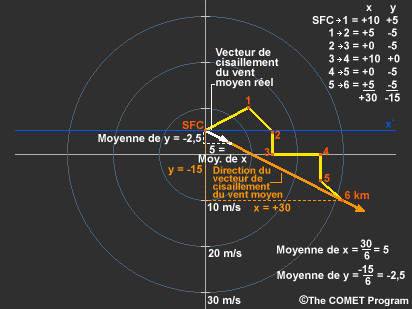
Le calcul du vecteur de cisaillement du vent moyen consiste simplement à calculer la moyenne des composantes x et y de chacun des vecteurs de cisaillement du vent dans chaque couche. Si nous examinons uniquement la direction du vecteur qui en résulte, et non son ampleur, nous pouvons ajouter les éléments x et y et représenter graphiquement la ligne en résultant, en se servant des vents de surface comme point d’origine du plan de référence x/y réorienté (x′). Le rapport x/y (direction) ne sera pas modifié en établissant la moyenne.
Sans établir la moyenne, la procédure est la même que l’exécution d’une addition des vecteurs de tous les vecteurs de cisaillement. C’est pour cette raison que nous pouvons toujours obtenir la direction du cisaillement du vent moyen en traçant une ligne à partir du premier tracé du vent et jusqu’au dernier pour la couche.
Le plan de référence réorienté (x′) indique que la direction du vecteur de cisaillement du vent moyen s’oriente vers le sud-est.
Forme de l’hodographe
Hodographes courbés et hodographes droits
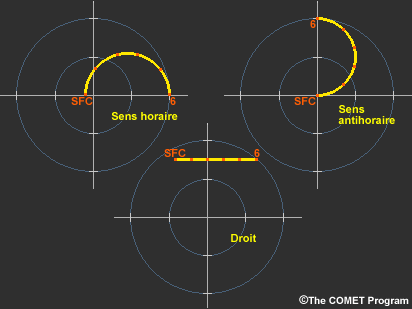
En plus de l’ampleur du cisaillement, la forme de l’hodographe est également importante pour prévoir la structure et l’évolution des tempêtes convectives. Le fait de savoir si l’hodographe est relativement droit ou courbé est d’une grande importance. S’il est courbé, son niveau de courbure et le fait de savoir s’il s’incurve dans le sens horaire ou antihoraire avec l’altitude sont importants. Ces variations ont toutes deux des répercussions sur la structure de la tempête.
Non-pertinence du cisaillement de vitesse par rapport au cisaillement directionnel
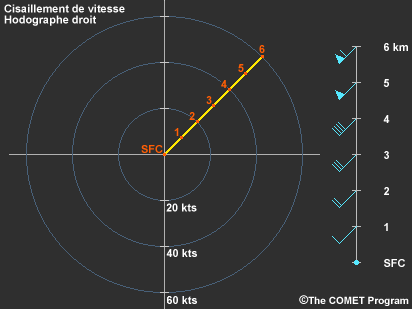
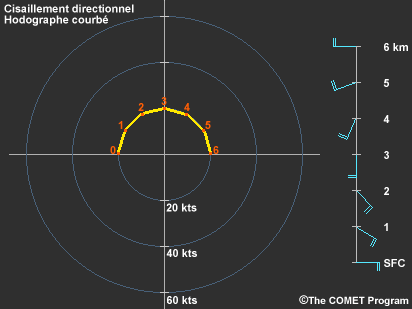
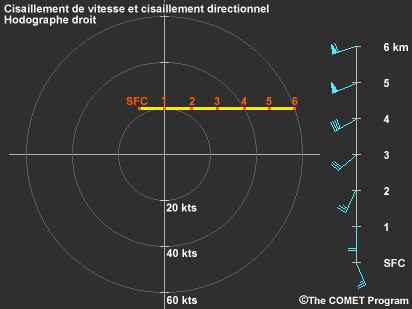
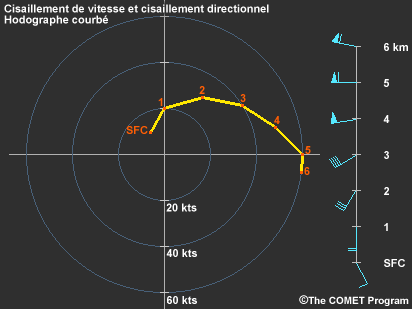
Nous savons que le cisaillement vertical du vent est créé à la fois par des changements dans la vitesse du vent avec l’altitude (cisaillement de vitesse) et des changements dans la direction du vent avec l’altitude (cisaillement directionnel). Le type de cisaillement, toutefois, nous renseigne peu sur la forme de l’hodographe étant donné qu’il fait référence à la vitesse et à la direction du vent et non à son vecteur de cisaillement.
Il est vrai que le cisaillement de vitesse à lui seul entraîne un hodographe droit (cisaillement unidirectionnel), et que le cisaillement directionnel également seul entraîne un hodographe courbé (le vecteur de cisaillement tourne avec l’altitude), mais la combinaison des deux peut créer n’importe quel type de forme.
Il faut comparer les types de cisaillement et la forme de l’hodographe.
Répercussions à grande échelle des hodographes
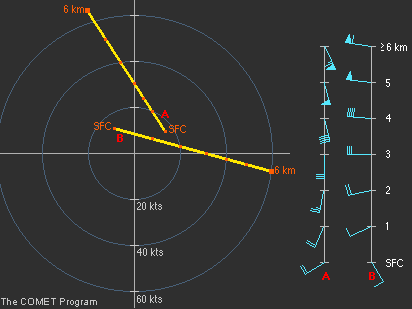
Tandis que les hodographes de forme similaire peuvent avoir une influence semblable sur l’évolution des tempêtes convectives, leurs répercussions sur les processus à plus grande échelle et le potentiel de convection peuvent différer considérablement.
Par exemple, les deux hodographes droits illustrés ici, pourraient vous mener à anticiper la division des supercellules si la convection se produisait. Toutefois, le cisaillement directionnel de l’hodographe A révèle un mouvement antihoraire jusqu’à une altitude moyenne, ce qui est le signe d’une advection d’air froid à grande échelle dans cette couche. L’hodographe B révèle des vents dans le sens horaire jusqu’à une altitude moyenne, ce qui indique une advection d’air chaud dans cette couche. Ces deux profils pourraient avoir des répercussions très différentes sur le potentiel de convection en fonction d’autres facteurs environnementaux. Par conséquent, il est très important de prendre en compte l’environnement à grande échelle lorsque vous analysez un hodographe.
Exercice : Représentation graphique des hodographes
Les exemples des pages précédentes devraient vous convaincre qu’il est difficile de visualiser la forme de l’hodographe en examinant les sondages. Pour cette raison, il est important d’utiliser un outil (comme un programme informatique tel que SHARP) pour créer un hodographe à votre place. Toutefois, il peut être utile d’être en mesure de produire rapidement ou de modifier un hodographe à la main. Ces exercices vous permettront de vous entraîner à cela.
Cliquez et dessinez sur l’emplacement de l’hodographe de chaque vent indiqué sur les sondages, dans l’ordre à partir de la surface jusqu’aux niveaux les plus élevés. Cliquez sur le bouton Terminé pour comparer vos résultats à la réponse corrigée.
Sélectionnez chacun des hodographes à tour de rôle pour mener à bien chaque partie de l’exercice.
Hodographe 1
Barbule pleine = 5 m/s, demi-barbule = 2,5 m/s
| Outil : | Taille de l’outil : | Couleur : |
|---|---|---|
Hodographe 2
Barbule pleine = 5 m/s, demi-barbule = 2,5 m/s
| Outil : | Taille de l’outil : | Couleur : |
|---|---|---|
Hodographe 3
Barbule pleine = 5 m/s, demi-barbule = 2,5 m/s
| Outil : | Taille de l’outil : | Couleur : |
|---|---|---|
En profondeur : Déplacement des tempêtes et vents relatifs aux tempêtes
Vents relatifs au sol et vents relatifs aux tempêtes
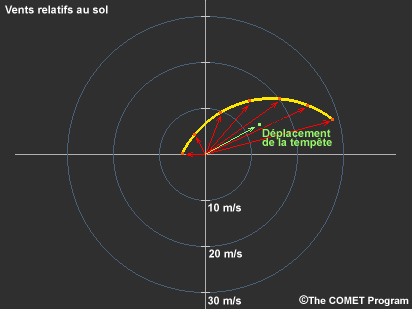
Afin de prévoir l’évolution d’une tempête convective, il est important de prendre en considération à la fois l’environnement dans lequel la tempête évolue actuellement ainsi que celui vers lequel elle peut se déplacer. Par exemple, la nature du courant entrant de la tempête a des répercussions sur son évolution.
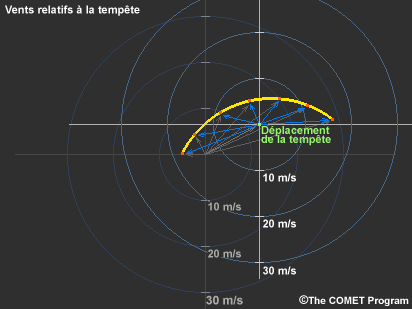
Afin de mieux comprendre cet élément de l’environnement de la tempête, vous devez tout d’abord déterminer ou estimer le déplacement prévu de la tempête sur l’hodographe, puis étudier les vents relatifs à celle-ci. Étant donné que la tempête se déplace dans son environnement, le vent qu’elle subit est souvent très différent des vents relatifs au sol mesurés par des sondages. Cette différence est évidente sur cet hodographe montrant le déplacement de la tempête.
Afin de déterminer les vents relatifs à la tempête, nous avons tout d’abord repositionné le plan de référence de sorte que le déplacement de la tempête soit nul. Ensuite, nous recalculons les vents de l’environnement à partir de ce point. Cela revient à soustraire le vecteur de déplacement de la tempête au niveau du sol au vecteur vent au niveau du sol à chaque altitude.
Déterminer le déplacement d’une tempête
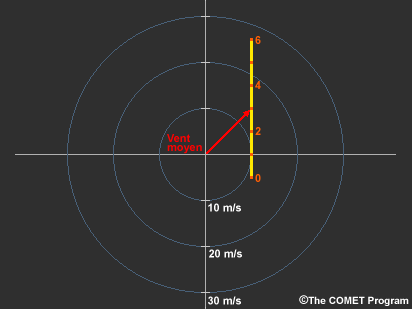
Afin d’étudier les vents relatifs à une tempête, vous devez tout d’abord déterminer le déplacement de la tempête. Pour les tempêtes existantes, on peut utiliser les boucles radar ou l’imagerie satellitaire. Mais pour prévoir le déplacement d’une tempête avant qu’elle se forme et avant que son déplacement soit apparent sur l’imagerie, vous allez devoir l’estimer.
On peut supposer, tout au moins aux premiers stades de la plupart des tempêtes convectives, que la tempête se déplace à une vitesse proche de celle du vent moyen se trouvant dans la profondeur de la tempête. Étant donné que la modélisation et les observations laissent entendre que le déplacement de la tempête est plus sensible aux vents à basse altitude, nous avons calculé le vent moyen au moyen d’une profondeur de 6 km (20 000 pi) au-dessus du niveau du sol. Le déplacement d’une supercellule s’écartera du vent moyen, mais ce sujet est traité dans un autre module.
Plusieurs progiciels (comme SHARP) calculent automatiquement le vent moyen, mais il est utile de comprendre de quelle façon cette opération est effectuée.
Estimation du déplacement d’une tempête : hodographe droit
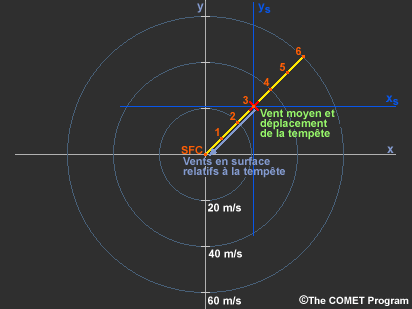
Lorsque l’hodographe est relativement droit, la règle du pouce pour estimer le vent moyen et le déplacement de la tempête est simple. Cela correspond environ au point central de l’hodographe de 0 à 6 km au-dessus du niveau du sol. Déterminer les vents relatifs à la tempête pour chaque altitude consiste alors à réorienter les axes (xs-ys) de manière à ce que le déplacement de la tempête soit nul. On détermine le vent relatif à la tempête à une altitude donnée, en dessinant un vecteur à partir de ce nouveau point d’origine jusqu’aux vents à cette altitude.
Pour être plus précis, on devra pondérer la pression des vents dans les bas niveaux. En raison de leur densité, ils contribueront davantage au déplacement de la tempête. Mais cela n’apporte qu’une légère modification à la véritable moyenne. De plus, nous tenons compte d’une bonne partie de l’anomalie en utilisant seulement les vents entre 0 et 6 km.
Formule permettant d’estimer le déplacement d’une tempête : hodographe courbé
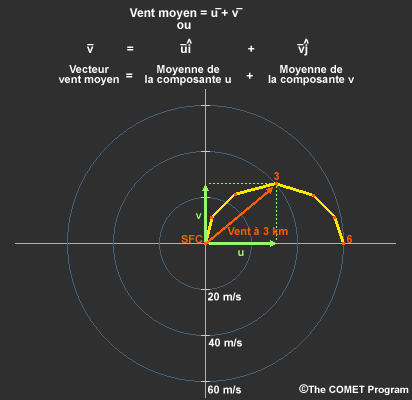
Lorsque l’hodographe s’incurve, l’estimation devient un peu plus compliquée. Nous devons examiner de plus près la façon dont le vent moyen est réellement calculé avant de pouvoir utiliser une règle empirique.
Chaque vecteur vent peut être décrit en présentant ses composantes u et v distinctes. Cette illustration montre une répartition des composantes du vent sur 3 km (10 000 pi).
Pour calculer le vent moyen, nous calculons séparément la moyenne des composantes u et v du vent moyen à toutes les altitudes. Nous additionnons ensuite les vecteurs moyens u et v. Dans la pratique, il ne s’agit pas d’un calcul rapide. Heureusement, l’hodographe vous permet de faire une approximation visuelle.
Procédure d’estimation du déplacement d’une tempête : hodographe courbé
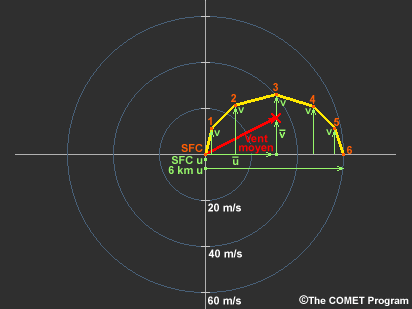
Pour illustrer la façon dont nous estimons le vent moyen à l’aide d’un hodographe, revenons à notre exemple d’hodographe courbé. Tout d’abord, vous pouvez constater que chaque point de l’hodographe possède des composantes u et v. Pour estimer la moyenne de la composante u, nous calculons simplement la moyenne des vents de la surface et à 6 km (20 000 pi). Cela suppose un espacement relativement égal des vents le long de l’hodographe, mais cela est adéquat pour obtenir une estimation approximative. Ensuite, nous estimons la moyenne des composantes v des vents à toutes les altitudes. En ajoutant les vecteurs u et v moyens, nous parvenons à une bonne estimation du vent moyen.
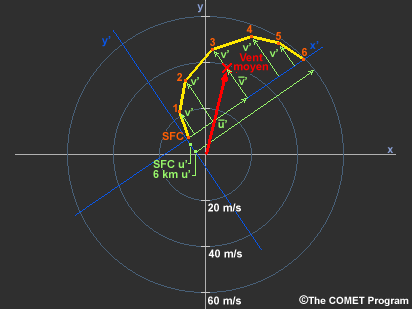
Cette technique fonctionne pour les hodographes se trouvant dans n’importe quelle orientation, mais vous devez en premier lieu réorienter le plan de référence x-y. Commencez par déplacer le point d’origine au niveau du point qui représente le vent de surface. Puis effectuez une rotation des axes x′-y′ de manière à ce que l’axe x′ coupe le vent de 6 km (20 000 pi). Estimez maintenant le vent moyen comme précédemment.
Estimation du déplacement d’une tempête : hodographe multicourbes
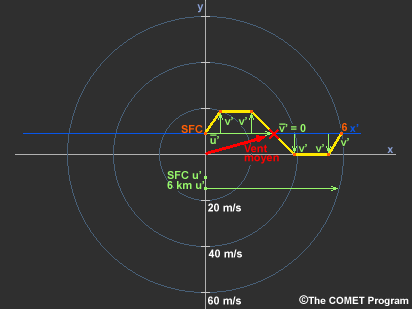
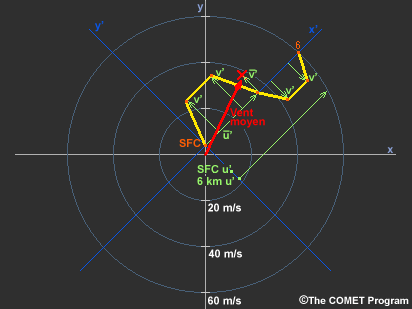
Lorsque l’hodographe présente une combinaison complexe de plusieurs courbes, cette stratégie peut vous aider à estimer le vent moyen, comme le montrent ces exemples. Il sera un peu plus compliqué de réaliser une bonne estimation de la moyenne de la composante v lorsque les courbes ne sont pas symétriques.
Exercice : Déterminer les vents de surface liés à une tempête
Question 1 de 3
Quel vecteur représente le mieux la direction (et non l’ampleur) des vents relatifs à la tempête? Supposons que la tempête se déplace avec le vent moyen. (Choisissez la meilleure réponse.)
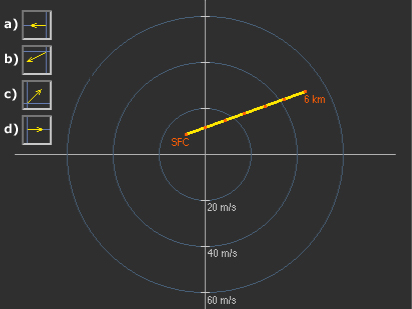
La bonne réponse est la réponse b).
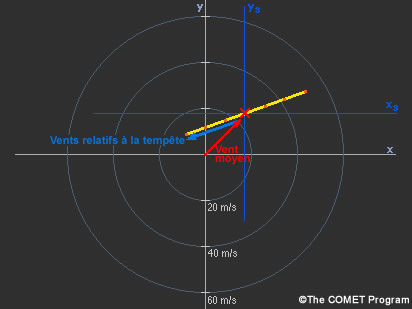
Examinez le diagramme pour voir de quelle manière nous déterminons le vent moyen au niveau du point central de l’hodographe droit de 0 à 6 km, puis nous réorientons le plan de référence x-y (xs-ys) pour représenter graphiquement le vent relatif à la tempête.
Question 2 de 3
Quel vecteur représente le mieux la direction (et non l’ampleur) des vents relatifs à la tempête? Supposons que la tempête se déplace avec le vent moyen. (Choisissez la meilleure réponse.)
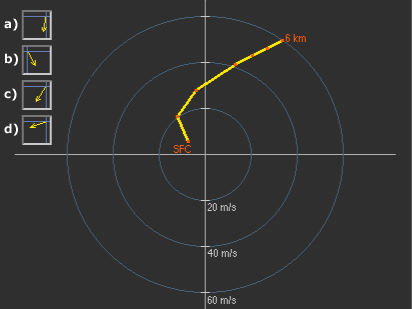
La bonne réponse est la réponse c).
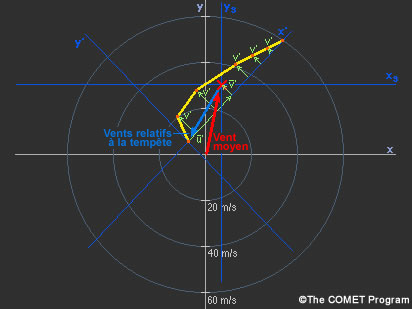
Examinez le diagramme pour voir de quelle manière nous déterminons le vent moyen au niveau du point central de l’hodographe droit de 0 à 6 km, puis nous réorientons le plan de référence x-y (xs-ys) pour représenter graphiquement le vent relatif à la tempête.
Question 3 de 3
Quel vecteur représente le mieux la direction (et non l’ampleur) des vents relatifs à la tempête? Supposons que la tempête se déplace avec le vent moyen. (Choisissez la meilleure réponse.)
La bonne réponse est la réponse c).
Examinez le diagramme pour voir de quelle manière nous déterminons le vent moyen au niveau du point central de l’hodographe droit de 0 à 6 km, puis nous réorientons le plan de référence x-y (xs-ys) pour représenter graphiquement le vent relatif à la tempête.

Résumé
- L’objet principal de l’hodographe consiste à indiquer le cisaillement vertical du vent.
- Le cisaillement vertical du vent est une description de la façon dont la vitesse du vent horizontal change en fonction de l’altitude. Nous déterminons le cisaillement vertical du vent en mesurant la différence vectorielle entre le vent horizontal à deux niveaux.
- L’hodographe s’appuie sur les vecteurs vent, plutôt que sur les barbules de vent. Pour créer un hodographe, les vecteurs vent sont indiqués sur un graphique à coordonnées polaires. Ensuite, leurs extrémités sont reliées.
- L’ampleur totale du cisaillement vertical du vent sur une certaine profondeur constitue un facteur important pour prévoir la structure et l’évolution de possibles tempêtes. L’estimation du cisaillement vertical total du vent s’effectue en combinant les longueurs de tous les vecteurs de cisaillement sur une certaine profondeur (la longueur nette de l’hodographe).
- Vous pouvez déterminer la direction du vecteur de cisaillement du vent moyen (mais pas l’ampleur) simplement en traçant une ligne à partir du point qui indique le vent de surface jusqu’au point indiquant le vent à 6 km (20 000 pi).
- Le calcul du vecteur de cisaillement du vent moyen consiste simplement à calculer la moyenne des composantes x et y de chacun des vecteurs de cisaillement du vent dans la chaque couche.
- En plus de l’ampleur du cisaillement, nous sommes également préoccupés par la question de savoir si l’hodographe est relativement droit ou courbé. Tandis que les hodographes de forme similaire peuvent avoir une incidence semblable sur l’évolution des tempêtes convectives, leurs répercussions sur les processus à plus grande échelle et le potentiel de convection peuvent différer considérablement.
- Étant donné que la tempête se déplace dans son environnement, le vent qu’elle subit est souvent très différent des vents de surface. Les vents relatifs à une tempête peuvent également être calculés sur un hodographe.
Dans ce module, nous avons appris comment calculer plusieurs paramètres différents du cisaillement et nous avons commencé à percevoir la façon dont ces paramètres sont appliqués. Pour en apprendre davantage sur l’importance et l’incidence du cisaillement sur les tempêtes convectives, consultez le module Principes de la convection III : Cisaillement et tempêtes convectives.
Collaborateurs
Commanditaires de COMET
The COMET® Program est parrainé par le National Weather Service (NWS) de la NOAA, et reçoit un financement supplémentaire de la part des entités suivantes:
- Bureau of Meteorology of Australia (BoM)
- Bureau of Reclamation, ministère de l’Intérieur des États-Unis
- Organisation européenne pour l’exploitation de satellites météorologiques (EUMETSAT)
- Service météorologique du Canada (SMC)
- NOAA’s National Environmental Satellite, Data and Information Service (NESDIS)
- NOAA’s National Geodetic Survey (NGS)
- Naval Meteorology and Oceanography Command (NMOC)
- U.S. Army Corps of Engineers (USACE)
Collaborateurs de projet
Chef de projet
- Dr. Doug Wesley — UCAR/COMET
Météorologue de projet
- Wendy Schreiber-Abshire — UCAR/COMET
Conception pédagogique / Création multimédia
- Dr. Alan Bol — UCAR/COMET
Conseillers scientifiques principaux
- CDR Robert Kiser — Naval Meteorology and Oceanography Professional Development Center (NAVMETOCPRODEVCEN) Staff at HQ AFWA/DNT 28th OWS Training Flight, Shaw AFB
- Kim Curry – Naval Pacific Meteorology and Oceanography Center - San Diego (NAVPACMETOCCEN)
- Dr. Thomas Lee — Naval Research Laboratory - Marine Meteorology Division (NRL-MMD)
- Dr. Wendell Nuss — Naval Postgraduate School
Infographie / Animations / Interface graphique
- Steve Deyo — UCAR/COMET
- Heidi Godsil — UCAR/COMET
Édition / production audio
- Seth Lamos — UCAR/COMET
Narration
- Wendy Schreiber-Abshire — UCAR/COMET
Traduction française
- Environnement Canada
Révision de la version française
- Nacéra Chergui — Météorologiste (SMC)
Narration française
- Hélène des Rosiers — HdR Translation & Editing Services
Images et photos fournies par
- NOAA/National Severe Storms Laboratory (NSSL)
Personnel du COMET, automne-hiver 2013-2014
Bureau du directeur
- Dr. Rich Jeffries, directeur
- Dr. Greg Byrd, directeur adjoint
Personnel administratif
- Elizabeth Lessard, gestionnaire de groupe
- Lorrie Alberta, administratrice
- Hildy Kane, adjointe administrative
Services de TI
- Tim Alberta, gestionnaire de groupe
- Bob Bubon, administrateur de systèmes
- Malte Winkler, ingénieur en logiciels
Services pédagogiques et services des médias
- Bruce Muller, gestionnaire de groupe
- Dr. Alan Bol, scientifique/concepteur pédagogique
- Steve Deyo, graphiste et concepteur 3D
- Lon Goldstein, concepteur pédagogique
- Bryan Guarente, météorologue/concepteur pédagogique
- Dan Riter, Software Engineer
- Tsvetomir Ross-Lazarov, concepteur pédagogique
- David Russi, traductions en espagnol
- Marianne Weingroff, concepteur pédagogique
Groupe scientifique
- Wendy Schreiber-Abshire, gestionnaire de groupe
- Dr. William Bua, météorologue
- Patrick Dills, météorologue
- Matthew Kelsch, Hydrometeorologist
- Dr. Elizabeth Mulvihill Page, météorologue
- Amy Stevermer, météorologue
Météorologues invités du Service météorologique du Canada
- Brad Snyder, MSC/COMET Liaison
- Nicolas Major, MSC/COMET Liaison