Uso de las mediciones de los instrumentos
Contamos con extensas y crecientes colecciones de mediciones relacionadas con los hidrometeoros y las partículas en suspensión, especialmente ahora que muchas agencias de financiación exigen que los archivos de datos recopilados en sus proyectos sean accesibles al público. Esta lección presenta principalmente los datos del repositorio de NCAR/EOL, que no es sino una de las muchas fuentes de datos disponibles. El objetivo de esta sección consiste en brindar orientación sobre el acceso a los datos archivados y su uso. La misma información se puede aplicar a los datos obtenidos directamente con los instrumentos descritos en las secciones precedentes.
Hace décadas que NCAR apoya la recolección de datos durante los proyectos de campo y, a solicitud, brinda acceso a los datos a través del repositorio de datos de EOL. Muchos de los datos archivados están en formato NetCDF que se describe en la página de la documentación de NetCDF. También encontrará información adicional sobre los archivos de datos generados por la aeronave de investigación en esta página sobre las convenciones de NCAR/RAF para NetCDF. Los datos de ejemplo empleados en los ejercicios de esta lección están en el formato .csv de hoja de cálculo. Los ejemplos de esta sección dependen de los datos provenientes de dicho repositorio.
Datos de concentraciones y distribución de tamaños
Haga clic aquí para descargar un ejemplo de un conjunto de datos de mediciones de 10 minutos obtenidos en una región de una nube, en formato de hoja de cálculo, cortesía de NCAR/EOL y con el patrocinio de la Fundación Nacional de Ciencias (National Science Foundation, NSF) de los EE.UU. Las mediciones marcadas «CONCD» y «CONC2DC» son valores de concentraciones obtenidos con la sonda de gotitas nubosas (Cloud Droplet Probe, CDP) y la sonda de matriz óptica 2D para nubes (2DC) que vimos en apartados anteriores. Las columnas «LWCC» y «LWCD» contienen las mediciones del contenido de agua líquida (g/m3) obtenidas con una sonda CSIRO/King y la CDP, respectivamente. Los valores que faltan en la columna «CONCD» no existían en el archivo de datos NetCDF original, de modo que una gráfica temporal de estas mediciones muestra períodos sin datos.
Puede utilizar esta hoja de cálculo con la herramienta de análisis de datos que prefiera para adquirir práctica en la construcción de gráficas de series temporales y otras formas de análisis de datos que involucran estas variables. Estos tipos de gráficas de serie temporal suelen ser el primer paso para poner en uso las mediciones de las propiedades de las nubes. A modo de ejemplo, estas tres gráficas se generaron a partir de esa misma hoja de datos.
Concentración de gotitas nubosas de la sonda CDP
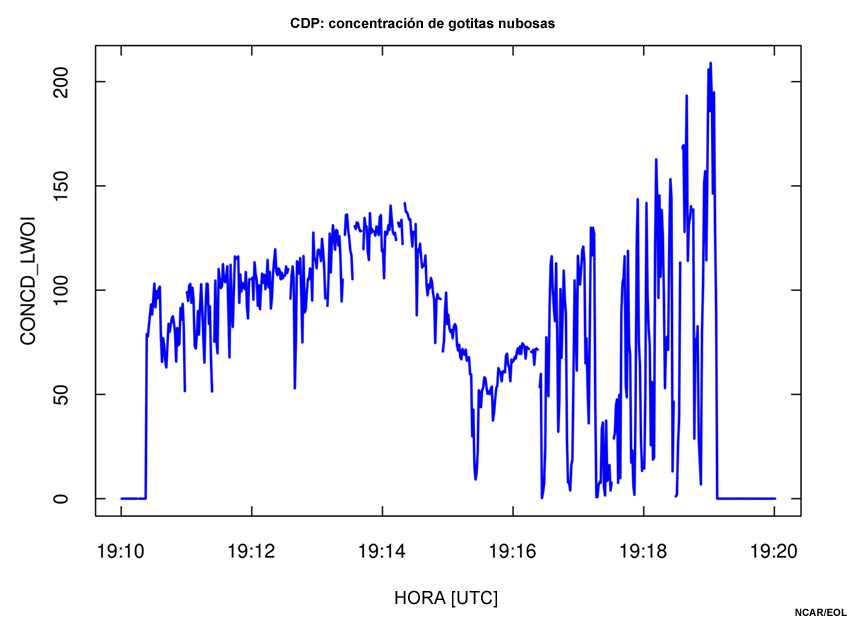
Concentración de gotitas nubosas medida el 17 de julio de 2015 con una sonda CDP mientras la aeronave de investigación atravesaba una nube en niveles bajos sobre el océano Pacífico. Siga el enlace a la hoja de cálculo al comienzo de esta página para descargar los datos de medición, que se representan en la variable «CONCD».
Mediciones de agua líquida en las nubes (LWCC y LWCD)
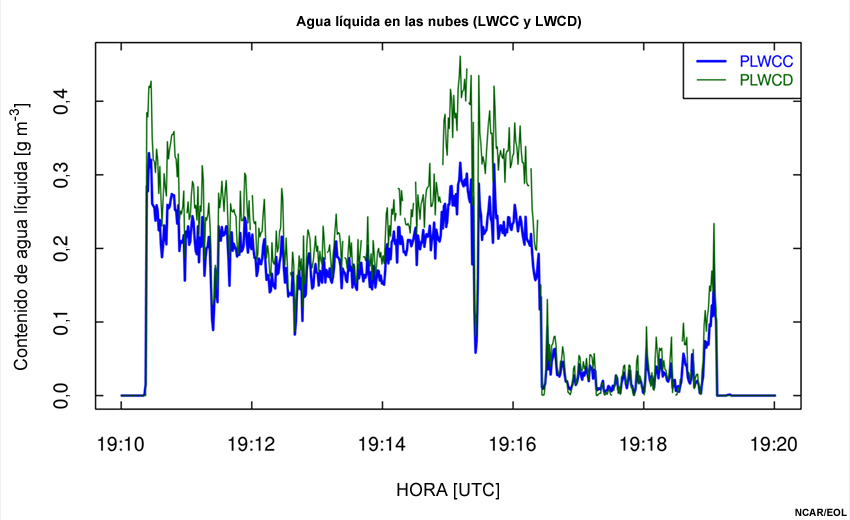
Dos mediciones de contenido de agua líquida en la nube obtenidas durante el mismo período indicado en la gráfica anterior. Las dos mediciones son «LWCC» y «LWCD» en la hoja de cálculo referenciada.
Comparación de las mediciones de agua líquida en las nubes de las sondas CDP y King
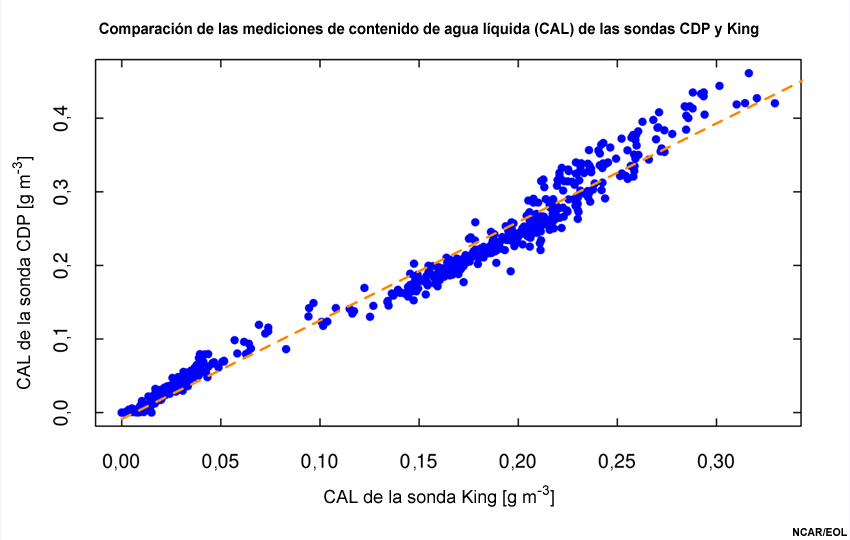
Comparación de los dos valores de contenido de agua líquida (CAL) de las sondas CSIRO/King y CDP. La gráfica utiliza las mismas mediciones usadas en la figura anterior. La línea de trazos color naranja se ajusta a una inclinación de 1,34.
Pregunta
De acuerdo con las figuras anteriores, ¿qué observa sobre las mediciones de las sondas CSIRO/King y CDP?
Las figuras y la curva de ajuste muestran claramente que el contenido de agua líquida medido con la sonda CDP es un 33 % más alto que el que se midió con la sonda CSIRO/King. Es probable que esto sea el resultado de errores de dimensionamiento en la sonda CDP, porque un error pequeño en el tamaño produce errores más grandes en el tercer momento estándar de los tamaños. Esta falta de coherencia puede indicar la necesidad de reajustar los niveles de umbral de la sonda CDP. Las pérdidas por coincidencia también pueden conducir a subestimar el contenido de agua líquida, aunque en este caso el error tiende a aumentar para concentraciones más altas y estas mediciones no parecen exhibir ninguna tendencia semejante.
Más sobre la distribución de tamaños
En un apartado anterior mencionamos la distribución diferencial de tamaños. Es útil examinar la relación entre la distribución de tamaños de las partículas y el contenido de agua líquida u otras características de la nube. En muchos casos, esta comparación se puede facilitar presentando la distribución de tamaños sobre ejes logarítmicos.
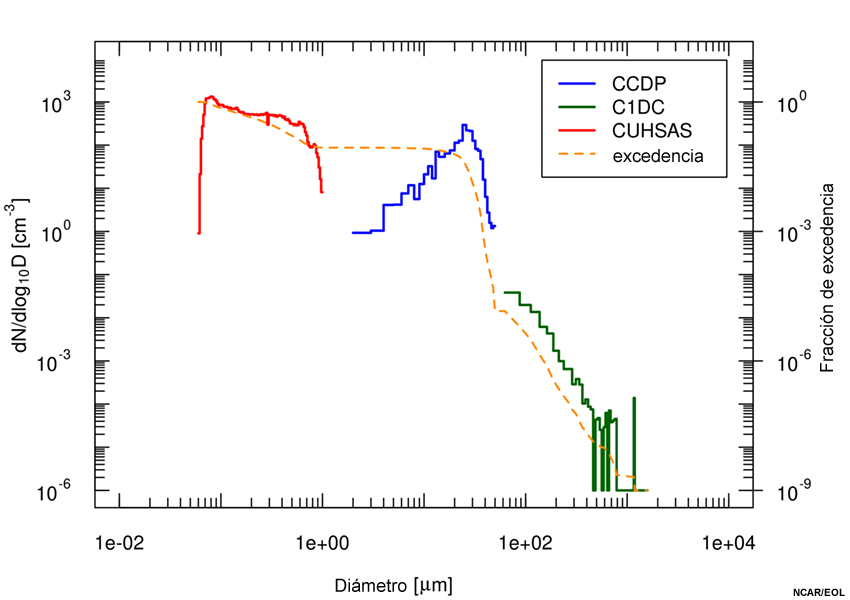
Ejemplo de una distribución diferencial de tamaños que representa las mediciones obtenidas con distintos instrumentos: una sonda CDP (la distribución de tamaños rotulada CCDP), una sonda 2DC (rotulada C1DC para indicar que se aplicó un estilo de procesamiento unidimensional a los datos 2DC, ya que se utilizó como tamaño estimado la dimensión máxima de las imágenes de las partículas en el sentido perpendicular al flujo de aire) y una sonda UHSAS (rotulada CUHSAS). Los pasos necesarios para generar esta gráfica se describen en las páginas que siguen. La fracción de excedencia es la fracción de partículas más grandes que el tamaño indicado y se grafica respecto del eje de la derecha en la figura.
Si usted trabaja con mediciones de distribución de tamaños, recomendamos que tenga en cuenta estas limitaciones:
- El paso coincidente de varias gotitas a través del haz láser puede causar errores considerables de dimensionamiento y de conteo. Si dos gotitas, una dentro y una fuera de la zona focal, coinciden, es posible que se acepten como una sola gotita de ese tamaño; también es posible que las gotitas que están fuera de la zona focal provoquen el rechazo de gotitas que realmente son válidas. Estos problemas de coincidencia pueden afectar la concentración máxima que se puede medir y distorsionar la distribución de tamaños medida, especialmente en las nubes «continentales», en las cuales se registran concentraciones típicas de gotitas de 500 cm-3 o más.
- Existen regiones de ambigüedad en la relación entre la sección de dispersión y el tamaño de la gotita similares a las que vimos antes en el diagrama de dispersión de Mie, aunque en este caso son más pronunciadas. Esta ambigüedad limita la resolución de tamaño de gotitas al rango de tamaños más pequeños.
- Es importante monitorear la calibración y la alineación óptica, porque la desalineación puede ocasionar errores. Es común usar bolitas de un tamaño y con un índice de refracción conocidos para comprobar la alineación y asegurar la calibración de tamaño correcta. La profundidad de campo también se puede comprobar inyectando bolitas desde un pequeño orificio o con un disco rotatorio y un objeto del tamaño de una gotita que gira para probar el funcionamiento de la sonda.
Encontrará mucha más información sobre este y otros contadores ópticos de partículas relacionados en la descripción de Wendisch y Brenguier (2013), sección 5.3.
Más sobre la distribución de tamaños » Distribución acumulada de tamaños
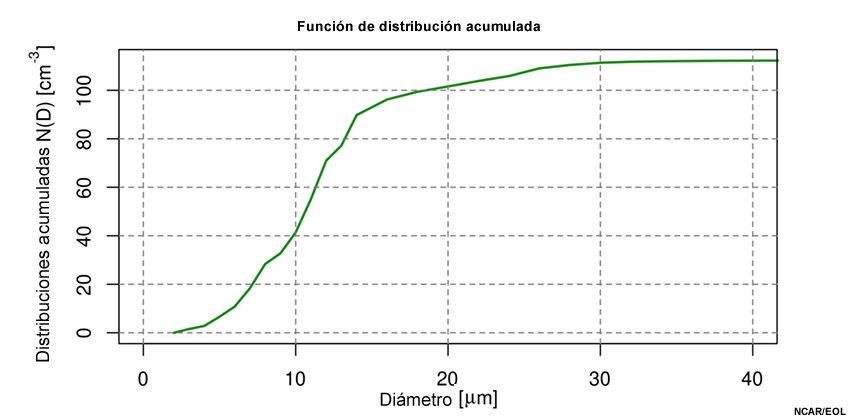
Esta función de distribución acumulada representa las mismas mediciones de la sonda CDP que vimos antes. Los valores de N(D) —la concentración total— aumentan desde 0 (los tamaños más pequeños) hasta 112 cm-3 (los tamaños más grandes). La distribución diferencial de tamaños correspondiente se muestra en la próxima página.
Es útil hablar primero de la distribución acumulada, porque las distribuciones diferenciales se pueden entender como derivadas de ella. Sea N(D) la concentración de gotitas con diámetros menores que D, como se muestra en la figura. De ahí procede que la distribución diferencial de tamaños n(D) viene dada por n(D) = dN(D)/dD; es decir, la derivada de la distribución acumulada da el cambio de concentración por unidad de cambio en el tamaño. Convertir de un histograma a una distribución diferencial de tamaños es fácil, simplemente se divide la concentración de cada intervalo por el intervalo de tamaños que representa.
Más sobre la distribución de tamaños » Cambio de variables y eje de abscisas logarítmico
Se puede presentar una distribución diferencial utilizando ejes logarítmicos, pero a menos que se modifique, se perderán características valiosas de un diagrama de distribución «adecuado». En los ejes lineales, el área debajo de la curva trazada es proporcional a la contribución de los varios intervalos de tamaños representados por la curva a la concentración total. Sin embargo, esta relación se pierde cuando el eje de las abscisas es logarítmico, de modo que se suele aplicar una modificación que conserva la relación con el área.
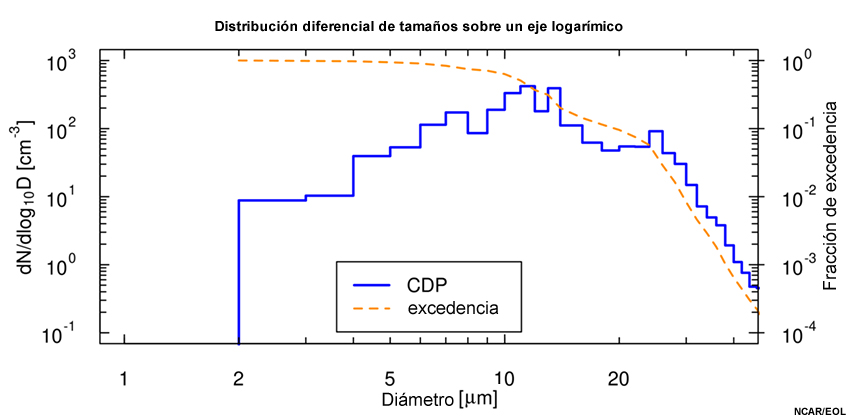
Función de distribución diferencial para las mediciones obtenidas con una sonda CDP trazada con un eje de las abscisas logarítmico. La curva de trazos color naranja identificada como «excedencia» se describe en la página siguiente.
Supongamos que lo que deseamos hallar es la distribución diferencial de tamaños en términos de una nueva variable x. Comience con la distribución acumulada N′(x) y tome la derivada para encontrar la distribución diferencial n′(x) a partir de n′(x) = dN′(x)/dx. La prima (′) indica que estas funciones difieren de N(D) y n(D). No obstante, para valores correspondientes de D y x, donde D se puede escribir como una función de x, las fracciones acumulativas deben ser equivalentes en términos de ambas variables: N(D(x)) = N′(x). La regla de la cadena conduce a n′(x) = dN′((x)/dx = (dN(D)/dD)(dD/dx) = n(D)(dD/dx). Esta nueva función de distribución será «adecuada» en el sentido de que el área de los intervalos de tamaños corresponderá a la contribución a la concentración de dichos intervalos de tamaños. Esta es la transformación general empleada en las siguientes definiciones de la nueva distribución de tamaños.
Específicamente, supongamos que x = log10 D, como sería deseable para un eje de las abscisas logarítmico. Luego, dx/dD = ln>e (10) d ln>e(D)/dD = ln>e(10) (1/D) o aproximadamente 2,30/D, de modo que n′(x) = n(D) (dD/dx) = n(D) D/2,30 da la función de distribución n′(log10(D)), donde áreas iguales en los intervalos logarítmicos dados aportan en igual medida a la concentración total. Ya presentamos varios ejemplos, incluido uno de esta misma distribución de tamaños en la página anterior.
Conviene tener presentes dos aspectos posiblemente problemáticos al examinar una distribución logarítmica de tamaños:
- A veces, la gráfica se presenta en términos de dD/dlne(D) en lugar de dD/dlog10(D), como en la gráfica anterior. Al utilizar estas distribuciones es importante determinar qué convención se está utilizando.
- Aunque la correspondencia de área rige si el eje de las ordenadas es lineal, en muchos casos es preferible usar un eje de las ordenadas logarítmico. Aunque es aún posible inferir las áreas correspondientes a diferentes intervalos de tamaños, es necesario tener en cuenta la escala logarítmica de las ordenadas.
Más sobre la distribución de tamaños » La fracción de excedencia
La fracción de distribución acumulada estándar es la función de distribución acumulada normalizada a razón de la concentración total y varía entre cero en el tamaño mínimo y la unidad en el tamaño máximo. Dado que a menudo resulta más interesante describir la fracción de tamaños grandes, se define una fracción complementaria —que aquí se denomina fracción «de excedencia»— como el complemento de la fracción de distribución acumulada que luego varía entre cero en el tamaño máximo y la unidad en el tamaño mínimo. Cuando se utilizan ejes logarítmicos, la fracción de excedencia tiene la ventaja de facilitar la identificación de las fracciones pequeñas que caracterizan los tamaños más grandes. La figura muestra un ejemplo en el cual las mediciones de las sondas CDP y 2DC se combinan en una misma gráfica.
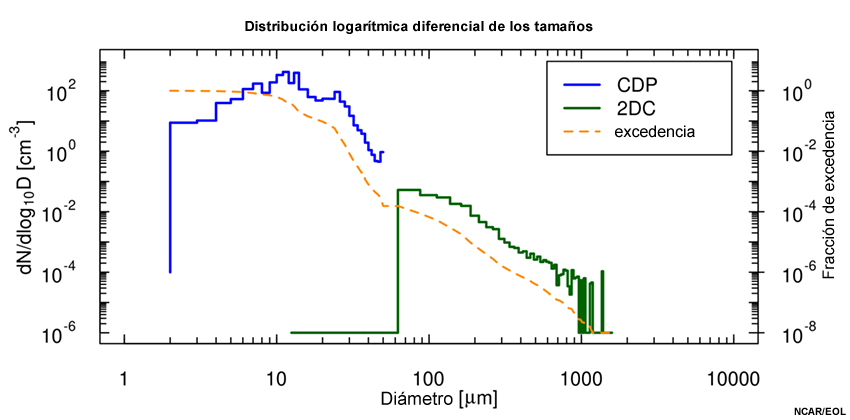
Esta distribución logarítmica diferencial muestra los tamaños de hidrometeoros medidos con dos instrumentos (una sonda CDP y una sonda 2DC) durante el mismo período que las gráficas precedentes. La curva de trazos color naranja es la fracción de excedencia, la fracción de los hidrometeoros con diámetros mayores que el tamaño indicado.
Mediciones derivadas de las distribuciones de tamaños
Entre las mediciones adicionales que se pueden obtener a partir de una distribución de tamaños de los hidrometeoros y las partículas en suspensión cabe mencionar las estimaciones de superficie, masa o volumen y reflectividad radar que se describen a continuación.
En el caso de un contador óptico de partículas, será preciso hacer algunas suposiciones sobre la forma y la composición de las partículas, a menos que se midan de forma independiente. Por ejemplo, si las partículas medidas son gotas de agua esféricas, el segundo, tercero y sexto momento de la distribución de tamaños conducen, respectivamente, a estimaciones de área, masa y factor de reflectividad radar. Tenga presente que las partículas de aerosol no son necesariamente esféricas y que las formas irregulares pueden afectar la capacidad de obtener magnitudes de orden superior a partir de la distribución de tamaños.
Dada una distribución diferencial de tamaños n(D), el jotaésimo momento se define como el valor promedio < D j >, donde los corchetes angulares indican la media. En términos de la distribución de tamaños, el jotaésimo momento viene dado por
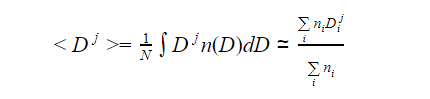
donde 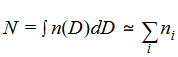 es la concentración total de
gotitas y ni es la concentración en
el intervalo de tamaños i que contiene el
tamaño Di. Luego, las propiedades
derivadas incluyen la información siguiente:
es la concentración total de
gotitas y ni es la concentración en
el intervalo de tamaños i que contiene el
tamaño Di. Luego, las propiedades
derivadas incluyen la información siguiente:
- el área de superficie total NπD2, que se obtiene a partir de la fórmula del área de superficie de una esfera (s = 4πr2);
- el contenido de agua líquida, definido como la masa de agua líquida por unidad de volumen;
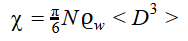 (del
volumen de una esfera,
(del
volumen de una esfera, 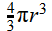 ), donde ϱ>w es la densidad del agua
líquida (≈ 1 g cm-3);
), donde ϱ>w es la densidad del agua
líquida (≈ 1 g cm-3);
- el «radio efectivo», que difiere del radio promedio; la razón entre el tercero y el segundo momento de una distribución de tamaños de gotitas.
Mediciones basadas en los momentos de distribución de tamaños
La extinción o el reflejo de la luz y el factor de reflectividad radar Z están relacionados con el segundo y el sexto momento de una distribución de tamaños de partículas n(D) en términos del diámetro D de las partículas, que se supone esférico. La tasa de precipitación R implica el producto del tercer momento (que determina el contenido de agua líquida) por la velocidad de caída, de modo que el momento que representa R incluye la velocidad de caída como factor de peso. Los efectos de dispersión y absorción de las partículas en suspensión influyen en el transporte de la radiación a través de la atmósfera, y la precipitación es el mecanismo principal que extrae agua de la atmósfera, de modo que las estimaciones de estos momentos constituyen un uso importante de las mediciones obtenidas con los medidores de partículas. Otro aspecto importante de los hidrometeoros es su aporte al albedo terrestre, el resultado de la eficacia con que pueden reflejar la radiación entrante.
Mediciones basadas en los momentos de distribución de tamaños » Algunas relaciones entre los momentos y las propiedades de las nubes
Estas son las ecuaciones para las propiedades de las nubes.
- Espesor óptico:
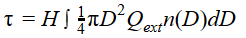 ,
donde 𝜏 es el espesor óptico, H es el espesor real de la capa a través de
la cual ocurre la distribución de tamaños especificada y Qext es el coeficiente de
extinción de la dispersión de Mie (una función de la longitud de onda) del tamaño de las
partículas y del complejo índice de refracción de las partículas. Sin el coeficiente de
extinción, para una capa delgada esto daría la proyección del área de dispersión de
partículas por área proyectada al final de la columna. Sin embargo, el coeficiente de
extinción varía considerablemente a través del rango normal de tamaños de las partículas en
suspensión, con valores entre ~0,05 o menos para las partículas finas y ~2 para las
partículas grandes en comparación con la longitud de onda de la luz. El coeficiente de
extinción es otra función importante del complejo índice de refracción de la partícula, de
modo que la incertidumbre en torno a esta propiedad de las partículas aumenta la
incertidumbre en el espesor óptico estimado. Cuando se calcula para la profundidad de toda
la atmósfera, normalmente esta propiedad se denomina «profundidad óptica»; la
fracción del flujo radiante en el límite de la atmósfera que se transmite a través de la
atmósfera es exp(-𝜏), donde 𝜏 es la profundidad óptica. Los valores típicos de
profundidad óptica oscilan entre menos de ~0,1 en una atmósfera limpia (en este caso un
90 % de la radiación entrante alcanza la superficie terrestre) y valores de 1 o más
en el caso de una atmósfera muy contaminada. Dado que la extinción a lo largo de la
trayectoria es exponencial, una profundidad óptica de 1 indica que 1/e de la radiación entrante alcanza la
superficie, es decir, aproximadamente el 37 %. Debido a esta atenuación exponencial,
la profundidad óptica puede exceder la unidad y cuando esto ocurre parte de la radiación
puede aún incidir en la superficie.
,
donde 𝜏 es el espesor óptico, H es el espesor real de la capa a través de
la cual ocurre la distribución de tamaños especificada y Qext es el coeficiente de
extinción de la dispersión de Mie (una función de la longitud de onda) del tamaño de las
partículas y del complejo índice de refracción de las partículas. Sin el coeficiente de
extinción, para una capa delgada esto daría la proyección del área de dispersión de
partículas por área proyectada al final de la columna. Sin embargo, el coeficiente de
extinción varía considerablemente a través del rango normal de tamaños de las partículas en
suspensión, con valores entre ~0,05 o menos para las partículas finas y ~2 para las
partículas grandes en comparación con la longitud de onda de la luz. El coeficiente de
extinción es otra función importante del complejo índice de refracción de la partícula, de
modo que la incertidumbre en torno a esta propiedad de las partículas aumenta la
incertidumbre en el espesor óptico estimado. Cuando se calcula para la profundidad de toda
la atmósfera, normalmente esta propiedad se denomina «profundidad óptica»; la
fracción del flujo radiante en el límite de la atmósfera que se transmite a través de la
atmósfera es exp(-𝜏), donde 𝜏 es la profundidad óptica. Los valores típicos de
profundidad óptica oscilan entre menos de ~0,1 en una atmósfera limpia (en este caso un
90 % de la radiación entrante alcanza la superficie terrestre) y valores de 1 o más
en el caso de una atmósfera muy contaminada. Dado que la extinción a lo largo de la
trayectoria es exponencial, una profundidad óptica de 1 indica que 1/e de la radiación entrante alcanza la
superficie, es decir, aproximadamente el 37 %. Debido a esta atenuación exponencial,
la profundidad óptica puede exceder la unidad y cuando esto ocurre parte de la radiación
puede aún incidir en la superficie. - Tasa de lluvia:
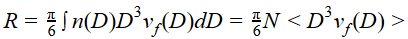 ,
donde N es la concentración de gotas de
lluvia, vf (D)
es la velocidad de caída de la gotas de diámetro D respecto de la Tierra y los corchetes
angulares indican el promedio de los valores del conjunto. Para las mediciones de tasa de
lluvia, por convención se suelen indicar estas mediciones en mm por hora.* Para las
mediciones in situ, a menudo es difícil determinar la velocidad de caída respecto
del suelo porque los hidrometeoros del tamaño de una gota de lluvia pueden no estar cayendo
a su velocidad de caída «terminal» (determinada por el equilibrio entre la
fuerza de la gravedad y la resistencia que opone el aire) y además pueden existir aportes
del movimiento vertical del aire. Sin embargo, la velocidad de caída terminal es bien
conocida y se puede usar para estimar la tasa de precipitación, sabiendo que estos efectos
pueden producir aportes adicionales.
,
donde N es la concentración de gotas de
lluvia, vf (D)
es la velocidad de caída de la gotas de diámetro D respecto de la Tierra y los corchetes
angulares indican el promedio de los valores del conjunto. Para las mediciones de tasa de
lluvia, por convención se suelen indicar estas mediciones en mm por hora.* Para las
mediciones in situ, a menudo es difícil determinar la velocidad de caída respecto
del suelo porque los hidrometeoros del tamaño de una gota de lluvia pueden no estar cayendo
a su velocidad de caída «terminal» (determinada por el equilibrio entre la
fuerza de la gravedad y la resistencia que opone el aire) y además pueden existir aportes
del movimiento vertical del aire. Sin embargo, la velocidad de caída terminal es bien
conocida y se puede usar para estimar la tasa de precipitación, sabiendo que estos efectos
pueden producir aportes adicionales. - Factor de reflectividad radar:
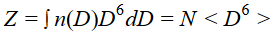 . Por convención, el
resultado se expresa en mm6m-3, de modo que se trata de seguir el
mismo proceso de conversión indicado en la nota del apartado anterior. Además, dado que la
variación en el resultado puede abarcar varios órdenes de magnitud, a menudo se expresa
después de esta conversión logarítmica: dB(Z) = 10log10(Z/Zr),
donde Zr es
1 mm6m-3. El factor Zr es un valor de referencia que a
menudo es implícito y se omite, pero que lógicamente se requiere para no calcular el
logaritmo de una magnitud dimensional. Es común ver la indicación de usar simplemente las
unidades convencionales [mm6m-3] en la ecuación de dB(Z).
. Por convención, el
resultado se expresa en mm6m-3, de modo que se trata de seguir el
mismo proceso de conversión indicado en la nota del apartado anterior. Además, dado que la
variación en el resultado puede abarcar varios órdenes de magnitud, a menudo se expresa
después de esta conversión logarítmica: dB(Z) = 10log10(Z/Zr),
donde Zr es
1 mm6m-3. El factor Zr es un valor de referencia que a
menudo es implícito y se omite, pero que lógicamente se requiere para no calcular el
logaritmo de una magnitud dimensional. Es común ver la indicación de usar simplemente las
unidades convencionales [mm6m-3] en la ecuación de dB(Z).
* Se precisa una conversión cuando las unidades que describen las mediciones básicas no concuerdan. En el caso de una distribución de tamaños medida con una sonda 2DC, los tamaños asignados a intervalos en la distribución de tamaños se suelen indicar en μm (10-6 m), pero las concentraciones se dan por litro (o 10-3 m). Resolver la ecuación para R requiere convertir primero tanto N como < D3 > a unidades SI, para que el producto sea adimensional. Esto implica multiplicar las propiedades medidas por (103 L/m3) × (10-6 m/μm)3. Luego, para calcular la profundidad de agua que se acumularía durante un período especificado se multiplica este resultado adimensional por la velocidad de caída. Si la velocidad de caída se midió en m/s, para obtener el resultado final en mm/h se precisa una conversión adicional: (103 mm/m) × (3600 s/h). Fíjese en el patrón general: todas las conversiones de unidades se pueden lograr efectuando una serie de multiplicaciones por factores de unidad como 103 L/m3 hasta haber convertido las unidades originales en las unidades finales deseadas.
Mediciones basadas en los momentos de distribución de tamaños » Aporte diferencial a los momentos
En muchos casos resulta útil graficar la distribución de las contribuciones a estos momentos. Por
ejemplo, si multiplicamos la distribución de tamaños por un factor apropiado (p. ej.: 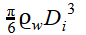 , para el
iésimo intervalo de tamaños) se
obtiene un trazado de la distribución de las contribuciones al contenido de agua líquida por
tamaño, como la que se muestra a continuación. Los tamaños pequeños registrados por el
instrumento UHSAS no constituyen un aporte significativo y los tamaños de la precipitación
indicados por el instrumento C1DC solo representan una contribución menor. El contenido de agua
líquida (aproximadamente 0,48 g m-3) ocurre casi por completo en las
gotitas nubosas medidas por la sonda CDP, especialmente las que tienen diámetros aproximados de
30 μm. Compare esta distribución con la correspondiente distribución diferencial de
tamaños.
, para el
iésimo intervalo de tamaños) se
obtiene un trazado de la distribución de las contribuciones al contenido de agua líquida por
tamaño, como la que se muestra a continuación. Los tamaños pequeños registrados por el
instrumento UHSAS no constituyen un aporte significativo y los tamaños de la precipitación
indicados por el instrumento C1DC solo representan una contribución menor. El contenido de agua
líquida (aproximadamente 0,48 g m-3) ocurre casi por completo en las
gotitas nubosas medidas por la sonda CDP, especialmente las que tienen diámetros aproximados de
30 μm. Compare esta distribución con la correspondiente distribución diferencial de
tamaños.
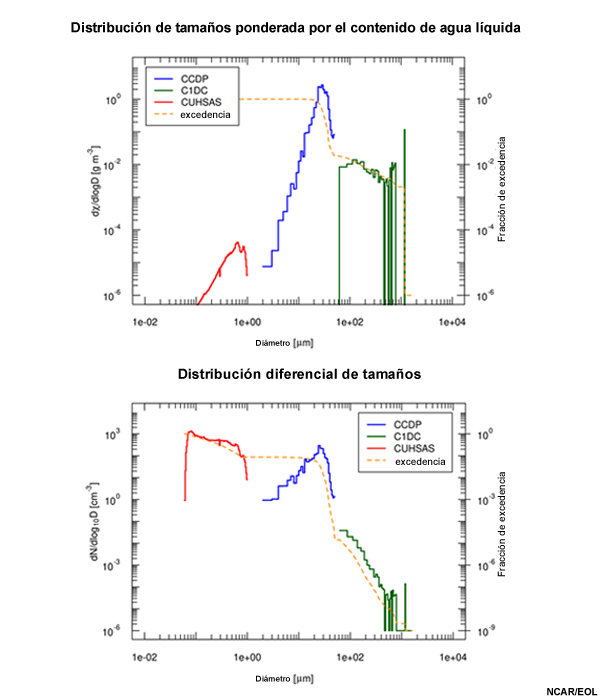
Estas dos gráficas utilizan las mismas mediciones: (arriba) las contribuciones al contenido de agua líquida (indicado por χ) de los hidrometeoros o gotitas de solución medidos con las sondas UHSAS, CDP o 2DC (rotuladas CUHSAS, CCDP y C1DC, respectivamente) en función del diámetro D de los hidrometeoros. La curva de trazos naranja es el complemento de la función de distribución acumulada, que aquí se denomina fracción de excedencia y se traza en relación con el eje derecho. Se expresa en unidades de g m-3 para el logaritmo base 10 del diámetro del hidrometeoro. (Abajo) Ejemplo de una distribución diferencial de tamaños en función del diámetro D de acuerdo con las mediciones de varios instrumentos: una sonda CDP (rotulada CCDP), una sonda 2DC (rotulada C1DC para indicar que los datos 2D se procesaron con métodos 1D) y una sonda UHSAS (CUHSAS).
Hay que tener presentes algunas fuentes de error especiales a la hora de calcular las propiedades a partir de los momentos:
- El tamaño medido de las partículas irregulares, como los hidrometeoros de hielo, no corresponde necesariamente al volumen de la partícula. Si bien es común utilizar relaciones empíricas entre el tamaño y la masa, la variación en la geometría cristalina y la densidad del graupel significan que siempre habrá un grado de incertidumbre asociado a dichas relaciones.
- Las gotas de lluvia grandes o que oscilan pueden adquirir formas no esféricas, lo cual puede conducir a errores en los momentos.
- Puede ser difícil estimar las propiedades de dispersión de la luz de las partículas de aerosol a partir de los momentos cuando se trata de partículas irregulares o de composición incierta.
- Cuando el tamaño se basa en la intensidad la luz dispersada, pueden ocurrir distorsiones hasta en la distribución de tamaños medida. Estas distorsiones a menudo se acentúan cuando se calculan los momentos.
A fin de estimar la incertidumbre aleatoria en momentos que surgen de una muestra finita, la fórmula siguiente puede proporcionar guía adicional acerca de la confiabilidad de la estimación del jotaésimo momento de la muestra:
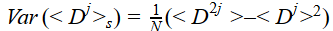
donde Var denota la varianza, el subíndice s recuerda que el momento es una estimación basada en una muestra finita y N es el número de observaciones en las que se basa la estimación.
Ejercicio: graficar la distribución y concentración de tamaños
Esta aplicación Shiny ofrece otros ejemplos de las distribuciones y concentraciones de tamaños obtenidas con varios medidores del tamaño de las partículas. Utilice los datos provistos para plotear las distribuciones de tamaños y concentraciones y luego conteste las preguntas que aparecen al final de esta página, que son las mismas que aparecen en la pestaña «Questions». Abra este panel para leer una descripción de la interfaz de la pestaña «Explore Data» en español y considere imprimir estas instrucciones para consultarlas al contestar las preguntas.
Esta aplicación interactiva permite examinar ciertos datos recolectados desde una aeronave de investigación mientras atravesaba una nube. Para generar las gráficas con esta aplicación, use los controles de la página «Explore Data»:
- Use el botón Download para descargar el conjunto de datos, lo cual le permitirá crear sus propias gráficas similares a las del ejercicio.
-
La lista desplegable variable to plot permite escoger distintos
tipos de mediciones. Las cinco opciones después de size distributions
fueron obtenidas con los instrumentos descritos en la lección: UHSAS
concentration, CDP concentration, 2DC concentration,
CSIRO/King LWC y CDP LWC.
- Escoja size distributions para generar la gráfica con los datos de las sondas activadas mediante las casillas probes to include in size distribution. Las dos opciones finales permiten usar escalas logarítmicas (log scales?) o trazar una distribución que muestra los aportes al contenido líquido de las nubes (LWC distribution?) en lugar de la concentración. En este caso, se supone que los objetos dimensionados con la sonda 2DC son gotas de agua esféricas.
- Con cualquiera de las otras opciones, la gráfica generada representa la serie temporal para esa variable.
- Para no borrar la última gráfica de la serie temporal al generar otra, active el botón no, add to exiting plot bajo new plot?. Esto permite agregar hasta seis variables diferentes en una misma gráfica, cada una de un color diferente. Esta opción solo funciona con series temporales.
- El control deslizante time interval de la parte superior del lado de la gráfica permite delimitar el subconjunto del período disponible a incluir en la gráfica. Esto afecta tanto las gráficas de serie temporal como las de distribuciones de tamaños.
- Debajo de las gráficas de distribuciones de tamaños se indican, en un renglón aparte, la concentración total y el contenido de agua líquida calculados a partir de dicha distribución de tamaños, suponiendo que todos los objetos sean esferas.
Las preguntas que aparecen al final de esta página de la lección son las mismas que aparecen en la pestaña «Questions». Si alguna de ellas le casusa dificultad, puede escribir el número de la pregunta en el campo show hints for this question number que aparece después de la lista de preguntas en la pestaña «Questions» para obtener una pista. Puede leer las pistas en español en el siguiente panel.
- En la lista desplegable variable to plot, escoja la opción size distributions y marque la casilla CDP. Puede variar el intervalo temporal para ver cómo varía la distribución de tamaños de gotitas a través de la nube.
- Examine la serie temporal de contenido de agua líquida (LWC).
- En la lista desplegable variable to plot, escoja la opción size distributions, active solo la casilla 2DC y luego active LWC distribution?. Para la segunda parte de la pregunta, active la distribución de tamaños solamente para el instrumento CDP.
- Visualice la distribución de tamaños del instrumento UHSAS y evalúe el contenido de agua líquida a partir del valor que aparece debajo de la gráfica.
- Visualice la serie temporal de temperatura y active el botón no, add to exiting plot bajo new plot?; a continuación, agregue la temperatura de punto de rocío (dew point) para trazar ambas curvas sobre la misma escala.
- Seleccione solamente los datos correspondientes al período pasado en la nube: visualice la serie temporal CDP-concentration y luego use los controles para delimitar el intervalo temporal a los períodos en la nube. Ahora visualice la distribución de tamaños del instrumento 2DC.
Si hace uso de estos datos en alguna publicación, siga este modelo para atribuir correctamente los derechos de autor de la fuente de datos:
UCAR/NCAR - Earth Observing Laboratory. 2018. Low Rate (LRT - 1 sps)
Navigation, State Parameter, and Microphysics Flight-Level Data. Version 1.3.
UCAR/NCAR - Earth Observing Laboratory.
https://doi.org/10.5065/D65Q4T96.
Acceso logrado el 29 de enero de 2019.
Datos proprocionados por NCAR/EOL bajo el patrocinio de la National Science Foundation.
https://data.eol.ucar.edu/
Ejercicio: momentos de la distribución de tamaños
Use la aplicación Shiny para contestar las preguntas siguientes.
Esta aplicación interactiva permite examinar más datos recolectados desde una aeronave de investigación, ya sea mientras atravesaba una nube o mientras atravesaba una columna de lluvia. Para descargar los conjuntos de datos, lo cual le permitirá utilizarlos para adquirir práctica y crear sus propias gráficas similares a las del ejercicio,en la página «Explore Data» escoja primero el conjunto cloud (nube) o (rain) (lluvia) bajo which data file? y luego haga clic en el botón Download. Este ejercicio se centra en las mediciones producidas mediante los momentos de las distribuciones de tamaños. La página «Explore Data» también permite generar gráficas que muestran el aporte de los tamaños individuales de la distribución a los distintos momentos que se describen en el numeral 5, más adelante. Considere imprimir estas instrucciones para consultarlas al contestar las preguntas.
Para generar las gráficas con esta aplicación, use los controles de la página «Explore Data»:
- Los botones bajo which data file? permiten escoger un vuelo a través de una nube densa (cloud) o de una columna de lluvia (rain). Esto permite comparar la diferencia en los momentos en esas regiones.
- La lista desplegable variable to plot permite escoger un conjunto de mediciones. Puede dejar el valor predeterminado size distributions (distribuciones de tamaños) tal cual, a menos que desee explorar algunas de las series temporales que se midieron.
- Cuando está seleccionada la opción size distributions, la gráfica se genera a partir de los datos de las sondas marcadas con las casillas debajo de probes to include in size distribution. Normalmente, conviene dejar activada la casilla log scales?, que permite utilizar escalas logarítmicas.
- El control deslizante de la parte superior del lado de la gráfica permite delimitar el subconjunto del período disponible a incluir en la gráfica.
- Para las distribuciones de tamaños puede escoger una de las distribuciones, a
saber:
- none - Produce la distribución de tamaños normal.
- Extinction - Muestra el segundo momento ponderado por el coeficiente de extinción de la dispersión de Mie. La información adicional acerca de esta opción que se incluye en la pestaña «Comments Regarding Extinction» aparece en español más adelante.
- LWC - Presenta la distribución de los aportes al contenido de agua líquida para distintas partes de la distribución de tamaños.
- Rain Rate - Muestra los aportes a la tasa de lluvia, suponiendo partículas esféricas que precipitan a su velocidad terminal.
- Radar Reflectivity - Muestra los aportes al factor de reflectividad radar.
En todos los casos, debajo de la gráfica se indica, en un renglón aparte, el aporte integrado a través de la distribución de tamaños. El factor de reflectividad radar se expresa en dB(Z) y para la extinción se indica la longitud de extinción.
Todas las gráficas incluyen la fracción de excedencia (exceedance fraction), que corresponde al eje vertical derecho. Esta información complementa la función de distribución acumulada y se puede usar para determinar la magnitud del aporte de las partículas de tamaño mayor que el tamaño ploteado.
Las preguntas que aparecen al final de esta página de la lección son las mismas que aparecen en la pestaña «Questions». Si alguna de ellas le casusa dificultad, puede escribir el número de la pregunta en el campo show hints for this question number que aparece después de la lista de preguntas en la pestaña «Questions» para obtener una pista. Puede leer las pistas en español en el siguiente panel.
- Deje sin cambiar los ajustes predeterminados y alterne entre los conjuntos de datos cloud y rain. Las características de los hidrometeoros son muy diferentes en las dos regiones. La concentración es mucho mayor en la primera (más de 100 cm-3) que en la segunda (típicamente cerca de 0.030 cm-3). Estas gráficas permiten comparar el contenido de agua líquida en las dos regiones.
- Agregue la distribución de tamaños para CDP, que representa las gotitas de lluvia, al aporte de 2DC para el conjunto de datos rain a fin de ver la medida en que las gotitas de lluvia aportan al contenido de agua líquida. Puede resultar útil delimitar el intervalo a las mediciones en el centro del vuelo a través de la región de lluvia. Para hacerlo, visualice una serie temporal como la concentración para 2DC y luego ajuste el control deslizante time interval en la parte superior del lado de la gráfica para delimitar la región de lluvia fuerte.
- Para establecer el conjunto de datos correcto y el intervalo temporal apropiado, escoja la distribución ponderada LWC y examine la distribución de fracción de excedencia.
- Escoja el conjunto de datos rain y la distribución ponderada Rain Rate y luego active la distribución de tamaños para 2DC. La gráfica resultante muestra que en el conjunto de datos de la región de lluvia el aporte de las gotas grandes a la tasa de lluvia es incluso más importante que su aporte al contenido de agua líquida. Delimite el intervalo temporal al período de lluvia más intensa para determinar la tasa de lluvia mása alta. Para la parte final de la pregunta, cambie al conjuntos de datos cloud.
- Escoja la distribución ponderada Radar Reflectivity y un intervalo temporal adecuado. En comparación con la región de lluvia, en este resultado aún predominan las gotas grandes y el aporte a la reflectividad de las gotas de lluvia con diámetros por debajo de aproximadamente 1 mm es escaso. La gráfica muestra la reflectividad calculada.
- Considere el conjunto de datos cloud con la ponderación Extinction y marque la casilla CDP para incluir las gotitas de nube en los cálculos. El índice de refracción predeterminado de 1.33+0i es adecuado para agua.
- Escoja el conjunto de datos rain para la sonda 2DC y active la ponderación Extinction para ver la extinción causada por esta lluvia bastante intensa. Ajuste el intervalo temporal para limitar la respusta a la parte más intensa del período en la región de lluvia.
- Estos datos se obtuvieron en sobre el océano Pacífico, al atravesar una zona de aire muy limpio. Antes de entrar en la nube, el instrumento UHSAS registró concentraciones de partículas que no excedían 250 por cm-3. Estas concentraciones tan bajas podrían levantar sospechas de un posible problema con las mediciones, pero suponiendo que la medición es válida, es útil considerar la extinción correspondiente. En la región antes de entrar en la nube, la longitud de extinción se puede evaluar sobre la base de algunas suposiciones acerca del índice de refracción (con luz de una longitud de onda de 560 nm). Dos posibles propuestas son 1.53+0.01i (que probablemente es razonable para partículas de sulfato) y 1.8+0.8i, para carbono negro (útil para considerar otro caso extremo, aunque es poco probable que predomine en esta región). Considere ambas posibilidades introduciendo los valores en el campo complex index of refraction con una longitud de onda de 560 nm. Escoja el conjunto de datos cloud y luego delimite los datos con el control deslizante a un período antes de entrar en la nube (p. ej.: 16:16:00 a 16:17:00). Escoja size distributions, marque solo la casilla UHSAS y active la ponderación Extinction para ver las longitudes de extinción resultantes, que se visualizan debajo de la gráfica. Use esos valores de extinción en la fórmula exponencial para la transmisión a fin de calcular la fracción de luz que se transmite a través de esta atmósfera, que se supone que abarque 15 km de altura.
Abra este panel para leer en español el texto de la pestaña Comments Regarding Extinction.
La opción de ponderación Extinction ofrece dos opciones adicionales:
- La opción wavelength (nm) for extinction calculation establece la longitud de onda empleada en los cálculos. El valor predeterminado de 560 nm cae cerca del medio del espectro de la luz visible.
- La opción complex index of refraction emplea un valor predeterminado de 1.33+0i (es decir: parte real de 1.33 e imaginaria de 0), apropriado para el agua a longitudes de onda visibles. Para ilustrar otro extremo, podría introducir 1.80+0.8i, un valor que podría ser apropiado para partículas de carbono negro muy absorbentes.
Como se explica en el cuerpo de la lección, la fórmula para calcular la
reducción en la intensidad de la luz I cuando una trayectoria
atraviesa una región densa dH es 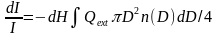 ,
donde Qext
es
el coeficiente de extinción adimensional. La integral tiene dimensiones
de área por volumen y, por tanto, de longitud inversa, de modo que
podemos considerar la inversa como una longitud de extinción: al pasar
por partículas con esta longitud de atenuación la intensidad se atenúa a
razón de 1/e. Luego, la
inversa de esta integral constituye una forma conveniente para
caracterizar el efecto de la población de partículas en la luz.
,
donde Qext
es
el coeficiente de extinción adimensional. La integral tiene dimensiones
de área por volumen y, por tanto, de longitud inversa, de modo que
podemos considerar la inversa como una longitud de extinción: al pasar
por partículas con esta longitud de atenuación la intensidad se atenúa a
razón de 1/e. Luego, la
inversa de esta integral constituye una forma conveniente para
caracterizar el efecto de la población de partículas en la luz.
En general, el coeficiente de extinción (que es una función del tamaño de
las partículas, del índice de refracción y de la longitud de onda) se
debe calcular a partir de ecuaciones de dispersión de Mie. No obstante,
hay dos regiones donde asume formas más simples: (a) para partículas
grandes respecto de la longitud de onda, donde Qext = 2
representa una buena aproximación, y (b) para partículas mucho más
pequeñas que la longitud de onda (la región de Rayleigh), donde la
dispersión es proporcional a la suma del cuadrado del volumen de las
partículas y la absorción es proporcional al volumen, con una
dependencia de la longitud de onda de dH de 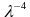 . El
valor de dispersión de Mie del coeficiente de extinción es calcula
siguiendo esta rutina, de mood que las variaciones en las propiedades
teóricas asignadas a las partículas o en la longitud de onda alterarán
los resultados.
. El
valor de dispersión de Mie del coeficiente de extinción es calcula
siguiendo esta rutina, de mood que las variaciones en las propiedades
teóricas asignadas a las partículas o en la longitud de onda alterarán
los resultados.
Si hace uso de estos datos en alguna publicación, siga este modelo para atribuir correctamente los derechos de autor de la fuente de datos:
UCAR/NCAR - Earth Observing Laboratory. 2018. Low Rate (LRT - 1 sps)
Navigation, State Parameter, and Microphysics Flight-Level Data. Version 1.3.
UCAR/NCAR - Earth Observing Laboratory.
https://doi.org/10.5065/D65Q4T96.
Acceso logrado el 29 de enero de 2019.
Datos proprocionados por NCAR/EOL bajo el patrocinio de la National Science
Foundation.
https://data.eol.ucar.edu/
Los valores de dispersión de Mie empleados en esta aplicación interactiva provienen del paquete «mie»: Baptiste Auguie (2014). mie: Mie scattering. R package version 1.0. https://github.com/plasmonics/mie
Uso de los archivos en formato NetCDF
Las aplicaciones Shiny interactivas de las páginas precedentes brindan acceso a los datos en un formato tabular adecuado para uso en una hoja de cálculo u otro programa de análisis. Sin embargo, este no es el formato empleado por la mayoría de las colecciones de datos. Un formato común es NetCDF, el mismo que se utiliza para todos los archivos de datos temporales generados con las aeronaves de investigación de NCAR. Como vimos antes, estos archivos se pueden obtener de los repositorios de NCAR y de las muchas otras organizaciones que apoyan las aeronaves de investigación y, a menudo, otros sistemas de observación terrestres similares. Estas sugerencias pueden ser útiles a la hora de trabajar con tales archivos.
- Use un programa auxiliar para convertir los archivos a un formato de texto o de tabla .csv.
Si NetCDF está instalado en su sistema, es probable que ya cuente con la herramienta
«ncdump», que puede producir listados de texto de variables y otra información
sobre el contenido de un archivo. Estos sitios ofrecen algunos recursos útiles:
- En un equipo Windows, la herramienta «netcdf4excel» puede importar muchos archivos en una hoja de cálculo.
- Si usted trabaja en «R», puede usar el paquete «ncdf4» para leer estos archivos en dicho programa.
- Si trabaja en Python, puede usar las herramientas similares de las rutinas NetCDF4-Python. Este enlace brinda acceso a un guion de Python que convierte archivos NetCDF al formato .csv. Este sitio web también contiene ejemplos muy útiles que pueden servir de guía. «xarray» (http://xarray.pydata.org/en/stable/) es otro buen recurso para trabajar con archivos NetCDF en Python. El lenguaje de comandos NCL (NCAR command language) también funciona con NetCDF.
- Muchos programas de análisis comerciales pueden leer los archivos directamente.
